机器学习实战---使用Apriori算法进行关联分析
一:参考资料
(一)机器学习实战或者见https://blog.csdn.net/qq_36523839/article/details/82191677
(二)Apriori算法是什么?适用于什么情境?(更好的理解关联规则)
(三)python中set和frozenset方法和区别
二:实现Apriori算法中的辅助函数
(一)加载数据
#1.加载数据 def loadDataSet(): return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] #模拟了多个(4)订单,每个订单中购买了不同的商品
(二)创建C1集合,是对各个订单数据统一统计,返回唯一的不重复的商品号
#2.创建C1集合,是对各个订单数据统一统计,返回唯一的不重复的商品号 def createC1(dataSet): C1 = [] #先设置为列表,表示可以改变 #注意:我们在C1列表中存放的还是列表,不是直接的数据 for dts in dataSet: for dt in dts: if not [dt] in C1: #注意:我们在C1列表中存放的还是列表,不是直接的数据 C1.append([dt]) C1.sort() #进行排序操作 return list(map(frozenset,C1)) #返回不可变集合(以为不可变集合可以作为字典键值使用),使用list将map转list
(三)根据数据集、和我们在createC1函数中获取的候选项集列表Ck,以及我们设置的支持度。返回满足最小支持度要求的集合
#3.根据数据集、和我们在createC1函数中获取的候选项集列表Ck,以及我们设置的支持度。返回满足最小支持度要求的集合 def scanD(D,Ck,minSupport): #D是数据集,由loadDataSet获取 ssCnt = {} #实现统计出现各个商品在多少个订单中出现 for tid in D: #遍历所有订单 for can in Ck: #遍历所有的商品号,是不可变集合类型 if can.issubset(tid): #如果是订单的子集,表示出现在一个订单中,可以+1计数 if not can in ssCnt: #py3没有has_key方法 # if not ssCnt.has_key(can): #注意:这就是我们要的不可变集合使用位置,是要作为字典的键 ssCnt[can] = 1 else: ssCnt[can] += 1 #计算各个商品的支持度,返回满足最小支持度的商品号 numItems = len(D) #计算所有订单数 retList = [] #返回所有满足最小支持度的商品号 supportData = {} #返回所有商品的支持度 for key in ssCnt.keys(): support = ssCnt[key] / numItems if support >= minSupport: retList.append(key) supportData[key] = support return retList,supportData
三:Apriori算法实现,获取候选频繁项集
(一)实现将多个列表合并(辅助Apriori算法):具体就是将多个n维列表合并维多个n+1维的列表
#二:Apriori算法实现 #1.实现将多个列表合并:具体就是将多个n维列表合并维多个n+1维的列表 #重点:我们要将多个n维列表合并维多个n+1维的列表,那么我们必须保证要合并的两个列表前n-1个数据是相同的,合并后才会变为n+1维 def aprioriGen(Lk,K): #实现合并,创造新的CK。注意:这里的K是只我们合并后列表的长度,Lk的实际长度是K-1 retList = [] lenLK = len(Lk) for i in range(lenLK): #进行遍历合并 for j in range(i+1,lenLK): L1 = list(Lk[i])[:K-2] #Lk的实际长度是K-1,所以我们只需要设置Lk的K-1-1即可 L2 = list(Lk[j])[:K-2] L1.sort() #之所以我们在这里进行排序,因为在createC1初始数据中,已经排序完成,后面新加入的数据也是自动排序的 L2.sort() #注释之后无影响 if L1==L2: retList.append(Lk[i] | Lk[j]) #注意对于frozenset类型,我们可以使用|进行并集操作,并且并集后的数据是排序后的 return retList #返回合并后维n+1维的列表数据
(二)实现Apriori算法
#2.实现Apriori算法 def apriori(dataSet,minSupport=0.5): #先获取初始数据 C1 = createC1(dataSet) #获取数据 D = list(map(set,dataSet)) #注意:我们需要使用list将数据从map转换为list #进行一次裁剪 L1,supportData = scanD(D,C1,minSupport) #开始进行循环处理 L = [L1] #将每一个维度的列表都放入列表中 K = 2 while len(L[K-2]) > 0: #从LK[0]即列表长度为1开始 Ck = aprioriGen(L[K-2],K) #进行合并操作 Lk,supportNewData = scanD(D,Ck,minSupport) #进行新的裁剪 #更新新的维度数据Lk的支持度 supportData.update(supportNewData) #对于没有的n+1维长度的列表,进行添加 L.append(Lk) #添加操作 K += 1 #注意:对于上面循环中,我们扩展到最后可能会出现,由于scanD方法中对于支持度较低的数据进行过滤,导致后面出现返回的Lk为空集,但是却更新了一次支持度(对最后面的n维列表更新) #所以必然L最后为[],导致len(LK[K-2])==0,退出循环 return L,supportData
(三)测试上述代码
#测试 dataset = loadDataSet() L,supportData = apriori(dataset,0.7)

L,supportData = apriori(dataset,0.5)
[[frozenset({1}), frozenset({3}), frozenset({2}), frozenset({5})], [frozenset({1, 3}), frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5})], [frozenset({2, 3, 5})], []]
四:基于上面的候选频繁项集,实现关联规则获取
(一)关联规则主函数实现
#三:从上面获取的频繁项集中挖掘出关联规则https://www.zhihu.com/question/19912364/answer/963934469?utm_source=wechat_session #注意:frozenset不可变集合是可以作为dict重点的key处理 a =frozenset({2, 5}) b = {a:1} #注意:frozenset可以进行多种运算,比如|,-... #1.关联规则生成函数 def generateRules(L,supportData,minConf=0.7): #L是我们上面apriori(dataset,0.7)求解的频繁项集,supportData是所有数据集的支持度信息,minConf是置信度 bigRuleList = [] #存放关联规则 注意:对于列表,字典等类型,通过函数可以进行修改 for i in range(1,len(L)): #我们只对列表有两个及以上的元素的集合进行关联处理(单个没有关联)比如i=1时:[frozenset({2, 5}),frozenset({3, 4})] for freqset in L[i]: #遍历集合中元素所有都是含有i+1个元素的列表的数据信息 frozenset({2, 5}) H1 = [frozenset([item]) for item in freqset] #注意:对应frozenset初始化,必须使用[]或者{} [frozenset({2}),frozenset({5})] if i > 1: #对于i>1,即集合中每个元素列表长度大于2,我们的规则可以有多种方法[a,b,c] a=>bc ac=>b ...,所以我们将其封装为一个函数 rulesFromConseq(freqset,H1,supportData,bigRuleList,minConf) else: #对于i=1时,表示有2两个元素在集合列表中,我们只包含一个映射[a,b] a=>b b=>a 单个元素之间的映射(通过calConf可以实现这一种映射) calConf(freqset,H1,supportData,bigRuleList,minConf) #计算置信度 #注意:calConf可以看做rulesFromConseq的辅助函数 return bigRuleList
(二)实现置信度求解函数
#2.辅助函数,计算置信度 def calConf(freqset,H1,supportData,bigRuleList,minConf): prunedH = [] #保存置信度 for conseq in H1: #置信度confidence=P(B|A)=P(AB)/P(A)),指的是发生事件A的基础上发生事件B的概率(相当与条件概率)。 conf = supportData[freqset] / supportData[freqset-conseq] #计算置信度看机器学习实战 if conf >= minConf: #大于最小置信度,打印并保存 print(freqset-conseq,"---->",conseq,conf) #打印前提条件,对于结果,置信度 bigRuleList.append((freqset-conseq,conseq,conf)) #保存规则 prunedH.append(conseq) #保存本次置信度检查中,满足最小置信度要求的规则,但是保存不全,后面也没有使用,应该不需要 return prunedH
(三)从初始的候选项集中,生成更多的数据集,进行关联规则查看,借助上面的函数计算置信度,也可以将两个函数合二为一
#3.从初始的候选项集中,生成更多的数据集,进行关联规则查看,借助上面的函数计算置信度,也可以将两个函数合二为一 def rulesFromConseq(freqset,H1,supportData,bigRuleList,minConf=0.7): #注意:在递归过程中,freqset不会变化,H1会随着合并增加 m = len(H1[0]) #查看当前输入的列表中,每个不可变集合元素个数 #查看频繁项是否可以大到可以移除大小为m的子集 if len(freqset) >= (m+1): #如果我们传入的原始freqset长度>m+1则可以正常递归,假设同上假设fregset为frozenset({2, 5}),H1为[frozenset({2}), frozenset({5})] #重点注意:len(freqset) > (m+1)中,如果len(freqset)=3,m=2呢??? #因此对比书本代码进行修改,使得可以出现a,b=>c的情况 Hmp1 = calConf(freqset,H1,supportData,bigRuleList,minConf) #根据我们合并的新的集合,进行置信度检测 Hmp1 = aprioriGen(Hmp1,m+1) #进行合并操作 if len(Hmp1) > 1: #继续递归,直到我们的函数不满足len(freqset) > (m+1)时退出 rulesFromConseq(freqset,Hmp1,supportData,bigRuleList,minConf)
(四)进行测试
L,supportData = apriori(dataset) rules = generateRules(L,supportData,0.5)
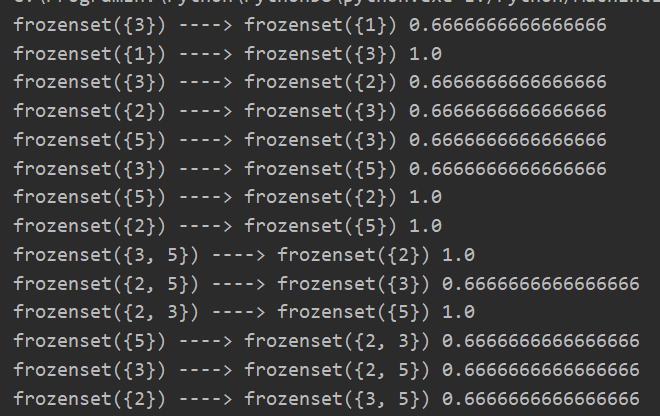
(五)全部代码

import numpy as np #一:实现Apriori算法中的辅助函数 #1.加载数据 def loadDataSet(): return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] #模拟了多个(4)订单,每个订单中购买了不同的商品 #2.创建C1集合,是对各个订单数据统一统计,返回唯一的不重复的商品号 def createC1(dataSet): C1 = [] #先设置为列表,表示可以改变 #注意:我们在C1列表中存放的还是列表,不是直接的数据 for dts in dataSet: for dt in dts: if not [dt] in C1: #注意:我们在C1列表中存放的还是列表,不是直接的数据 C1.append([dt]) C1.sort() #进行排序操作 return list(map(frozenset,C1)) #返回不可变集合(以为不可变集合可以作为字典键值使用),使用list将map转list #3.根据数据集、和我们在createC1函数中获取的候选项集列表Ck,以及我们设置的支持度。返回满足最小支持度要求的集合 def scanD(D,Ck,minSupport): #D是数据集,由loadDataSet获取 ssCnt = {} #实现统计出现各个商品在多少个订单中出现 for tid in D: #遍历所有订单 for can in Ck: #遍历所有的商品号,是不可变集合类型 if can.issubset(tid): #如果是订单的子集,表示出现在一个订单中,可以+1计数 if not can in ssCnt: #py3没有has_key方法 # if not ssCnt.has_key(can): #注意:这就是我们要的不可变集合使用位置,是要作为字典的键 ssCnt[can] = 1 else: ssCnt[can] += 1 #计算各个商品的支持度,返回满足最小支持度的商品号 numItems = len(D) #计算所有订单数 retList = [] #返回所有满足最小支持度的商品号 supportData = {} #返回所有商品的支持度 for key in ssCnt.keys(): support = ssCnt[key] / numItems if support >= minSupport: retList.append(key) supportData[key] = support return retList,supportData #二:Apriori算法实现 #1.实现将多个列表合并:具体就是将多个n维列表合并维多个n+1维的列表 #重点:我们要将多个n维列表合并维多个n+1维的列表,那么我们必须保证要合并的两个列表前n-1个数据是相同的,合并后才会变为n+1维 def aprioriGen(Lk,K): #实现合并,创造新的CK。注意:这里的K是只我们合并后列表的长度,Lk的实际长度是K-1 retList = [] lenLK = len(Lk) for i in range(lenLK): #进行遍历合并 for j in range(i+1,lenLK): L1 = list(Lk[i])[:K-2] #Lk的实际长度是K-1,所以我们只需要设置Lk的K-1-1即可 L2 = list(Lk[j])[:K-2] L1.sort() #之所以我们在这里进行排序,因为在createC1初始数据中,已经排序完成,后面新加入的数据也是自动排序的 L2.sort() #注释之后无影响 if L1==L2: retList.append(Lk[i] | Lk[j]) #注意对于frozenset类型,我们可以使用|进行并集操作,并且并集后的数据是排序后的 return retList #返回合并后维n+1维的列表数据 #2.实现Apriori算法 def apriori(dataSet,minSupport=0.5): #先获取初始数据 C1 = createC1(dataSet) #获取数据 D = list(map(set,dataSet)) #注意:我们需要使用list将数据从map转换为list #进行一次裁剪 L1,supportData = scanD(D,C1,minSupport) #开始进行循环处理 L = [L1] #将每一个维度的列表都放入列表中 K = 2 while len(L[K-2]) > 0: #从LK[0]即列表长度为1开始 Ck = aprioriGen(L[K-2],K) #进行合并操作 Lk,supportNewData = scanD(D,Ck,minSupport) #进行新的裁剪 #更新新的维度数据Lk的支持度 supportData.update(supportNewData) #对于没有的n+1维长度的列表,进行添加 L.append(Lk) #添加操作 K += 1 #注意:对于上面循环中,我们扩展到最后可能会出现,由于scanD方法中对于支持度较低的数据进行过滤,导致后面出现返回的Lk为空集,但是却更新了一次支持度(对最后面的n维列表更新) #所以必然L最后为[],导致len(LK[K-2])==0,退出循环 return L,supportData #测试 dataset = loadDataSet() # L,supportData = apriori(dataset,0.5) # print(L) #[[frozenset({1}), frozenset({3}), frozenset({2}), frozenset({5})], [frozenset({1, 3}), frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5})], [frozenset({2, 3, 5})], []] #三:从上面获取的频繁项集中挖掘出关联规则https://www.zhihu.com/question/19912364/answer/963934469?utm_source=wechat_session #注意:frozenset不可变集合是可以作为dict重点的key处理 a =frozenset({2, 5}) b = {a:1} #注意:frozenset可以进行多种运算,比如|,-... #1.关联规则生成函数 def generateRules(L,supportData,minConf=0.7): #L是我们上面apriori(dataset,0.7)求解的频繁项集,supportData是所有数据集的支持度信息,minConf是置信度 bigRuleList = [] #存放关联规则 注意:对于列表,字典等类型,通过函数可以进行修改 for i in range(1,len(L)): #我们只对列表有两个及以上的元素的集合进行关联处理(单个没有关联)比如i=1时:[frozenset({2, 5}),frozenset({3, 4})] for freqset in L[i]: #遍历集合中元素所有都是含有i+1个元素的列表的数据信息 frozenset({2, 5}) H1 = [frozenset([item]) for item in freqset] #注意:对应frozenset初始化,必须使用[]或者{} [frozenset({2}),frozenset({5})] if i > 1: #对于i>1,即集合中每个元素列表长度大于2,我们的规则可以有多种方法[a,b,c] a=>bc ac=>b ...,所以我们将其封装为一个函数 rulesFromConseq(freqset,H1,supportData,bigRuleList,minConf) else: #对于i=1时,表示有2两个元素在集合列表中,我们只包含一个映射[a,b] a=>b b=>a 单个元素之间的映射(通过calConf可以实现这一种映射) calConf(freqset,H1,supportData,bigRuleList,minConf) #计算置信度 #注意:calConf可以看做rulesFromConseq的辅助函数 return bigRuleList #2.辅助函数,计算置信度 def calConf(freqset,H1,supportData,bigRuleList,minConf): prunedH = [] #保存置信度 for conseq in H1: #置信度confidence=P(B|A)=P(AB)/P(A)),指的是发生事件A的基础上发生事件B的概率(相当与条件概率)。 conf = supportData[freqset] / supportData[freqset-conseq] #计算置信度看机器学习实战 if conf >= minConf: #大于最小置信度,打印并保存 print(freqset-conseq,"---->",conseq,conf) #打印前提条件,对于结果,置信度 bigRuleList.append((freqset-conseq,conseq,conf)) #保存规则 prunedH.append(conseq) #保存本次置信度检查中,满足最小置信度要求的规则,但是保存不全,后面也没有使用,应该不需要 return prunedH #3.从初始的候选项集中,生成更多的数据集,进行关联规则查看,借助上面的函数计算置信度,也可以将两个函数合二为一 def rulesFromConseq(freqset,H1,supportData,bigRuleList,minConf=0.7): #注意:在递归过程中,freqset不会变化,H1会随着合并增加 m = len(H1[0]) #查看当前输入的列表中,每个不可变集合元素个数 #查看频繁项是否可以大到可以移除大小为m的子集 if len(freqset) >= (m+1): #如果我们传入的原始freqset长度>m+1则可以正常递归,假设同上假设fregset为frozenset({2, 5}),H1为[frozenset({2}), frozenset({5})] #重点注意:len(freqset) > (m+1)中,如果len(freqset)=3,m=2呢??? #因此对比书本代码进行修改,使得可以出现a,b=>c的情况 Hmp1 = calConf(freqset,H1,supportData,bigRuleList,minConf) #根据我们合并的新的集合,进行置信度检测 Hmp1 = aprioriGen(Hmp1,m+1) #进行合并操作 if len(Hmp1) > 1: #继续递归,直到我们的函数不满足len(freqset) > (m+1)时退出 rulesFromConseq(freqset,Hmp1,supportData,bigRuleList,minConf) L,supportData = apriori(dataset) rules = generateRules(L,supportData,0.5)
五:总结
Apriori算法简单,易于实现。但是它也有自己的缺点,数据集很大的时会出现下面两个问题。
1. 需要多次扫描数据集
例如在Apriori算法循环中:即每次增加新的频繁项集的时候,Apriori算法都会重新扫描整个数据集
Lk,supportNewData = scanD(D,Ck,minSupport) #进行新的裁剪
或者后面求解的支持度(针对每个数据都存在支持度),也存在多次扫描
2. 可能会产生庞大的候选集
当数据极大,支持度设置太小时
3.FP-growth算法引出
针对Apriori算法的性能瓶颈问题,2000年Jiawei Han等人提出了基于FP树生成频繁项集的FP-growth算法。该算法只进行2次数据库扫描且它不使用侯选集,直接压缩数据库成一个频繁模式树,最后通过这棵树生成关联规则。
研究表明它比Apriori算法大约快一个数量级。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号