机器学习实战---决策树ID3算法
一:代码实现
import numpy as np from math import log
(一)创建数据集
# 创建数据集 def createDataSet(): dataSet = [[1, 1], [1, 1], [1, 0], [0, 1], [0, 1]] labels = [1, 1, 0, 0, 0] features_names = ['水下', '脚蹼'] # 特征名称 return dataSet, labels, features_names
(二)计算信息熵
#计算信息熵 def calcEnt(data_Y): #传入numpy数据 cnt = len(data_Y) EntVal = 0.0 val_nums = np.unique(data_Y) for val in val_nums: num = data_Y[np.where(data_Y==val)].size EntVal += num/cnt*log(num/cnt,2) return -EntVal
(三)根据信息增益获取特征
#根据信息熵,获取最好的特征 def chooseBestFeature(data_X,data_Y): samp_num,fea_num = data_X.shape #统计样本数、特征数 #循环统计每个特征的信息增益 BaseEntval = calcEnt(data_Y) BestFeature = -1;BestEntGain=0.0 for i in range(fea_num): #开始循环特征 newEntVal = 0.0 #获取每个特征的信息熵 val_nums = np.unique(data_X[:,i]) #先获取该特征下的值种类 for val in val_nums: new_dataY = data_Y[np.where(data_X[:, i] == val)] newEntVal += new_dataY.size/samp_num*calcEnt(new_dataY) if BaseEntval - newEntVal > BestEntGain: #比较信息增益大小 BestEntGain = BaseEntval - newEntVal BestFeature = i return BestFeature
(四)按特征和特征的值进行子集划分
#按特征和特征的值进行子集划分 注意:最后返回的子集中不包含原来的特征 def splitDataByFeature(data_X,data_Y,fea_idx,fea_axis,fea_val): #注意fea_idx保存了特征原始索引 new_dataX = data_X[np.where(data_X[:,fea_axis]==fea_val)] new_dataY = data_Y[np.where(data_X[:, fea_axis] == fea_val)] new_dataX = np.delete(new_dataX,fea_axis,1) #按列删除特征 new_feaIdx = np.delete(fea_idx,fea_axis,0) #按行删除 (2,) return new_dataX,new_dataY,new_feaIdx #因为先获取了new_dataY,之后才删除的该特征列,所以必然存在new_dataX为空,new_dataY不为空情况
(五)创建决策树
#开始递归创建树 def createTree(data_X,data_Y,fea_idx): y_valNums = np.unique(data_Y) #值去重 if y_valNums.size == 1: #全是一个类别,直接返回该类别 return np.int(data_Y[0]) if data_X.shape[1] == 0: #如果该递归路径下,已经遍历了所有特征,使用多数投票进行分类返回(这里和splitDataByFeature有关) bestCls,bestCnt = 0,0 for i in y_valNums: if data_Y[np.where(data_Y==i)].size > bestCnt: bestCls = i return bestCls #可以进行递归了 BestFeature = chooseBestFeature(data_X,data_Y) my_tree = {fea_idx[BestFeature]:{}} uniFeaVals = np.unique(data_X[:,BestFeature]) for i in uniFeaVals: new_dataX,new_dataY,new_feaIdx = splitDataByFeature(data_X,data_Y,fea_idx,BestFeature,i) #获取新的划分子集,注意,因为我们是先获取Y标签,然后才删除X矩阵该特征列。所以会出现data_X为空,data_Y不为空情况 my_tree[fea_idx[BestFeature]][i] = createTree(new_dataX,new_dataY,new_feaIdx) return my_tree
(六)实现预测
def classify(inputTree,testVec): #递归查找树,直到找到叶子节点 rootTag = list(inputTree.keys())[0] #获取根节点信息,看先找的哪一个特征 --- 获取索引 FeaVal = inputTree[rootTag] #获取该根节点全部特性值 --- 获取值 for k in FeaVal.keys(): if k == testVec[rootTag]: if type(inputTree[rootTag][k]) != dict: return inputTree[rootTag][k] return classify(inputTree[rootTag][k],testVec)
(七)进行测试
data_x,data_y,fea_names = createDataSet() fea_Idx = np.arange(len(fea_names)) data_X,data_Y = np.array(data_x),np.array([data_y]).T myTree = createTree(data_X,data_Y,fea_Idx) print(myTree) testData = np.zeros(len(fea_names)) for i in range(len(fea_names)): testData[i] = input("{}(0/1)>:".format(fea_names[i])) print(classify(myTree,testData))
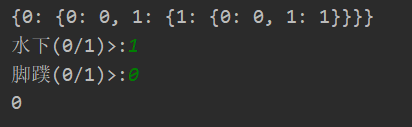
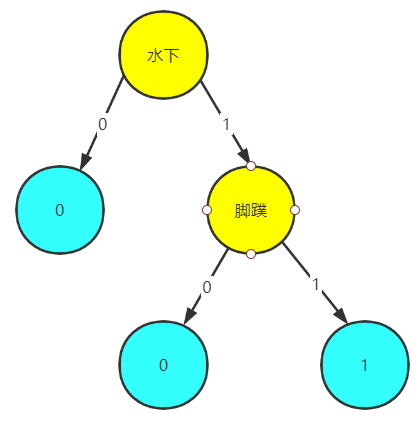
(八)全部代码

import numpy as np from math import log # 创建数据集 def createDataSet(): dataSet = [[1, 1], [1, 1], [1, 0], [0, 1], [0, 1]] labels = [1, 1, 0, 0, 0] features_names = ['水下', '脚蹼'] # 特征名称 return dataSet, labels, features_names #计算信息熵 def calcEnt(data_Y): #传入numpy数据 cnt = len(data_Y) EntVal = 0.0 val_nums = np.unique(data_Y) for val in val_nums: num = data_Y[np.where(data_Y==val)].size EntVal += num/cnt*log(num/cnt,2) return -EntVal #根据信息熵,获取最好的特征 def chooseBestFeature(data_X,data_Y): samp_num,fea_num = data_X.shape #统计样本数、特征数 #循环统计每个特征的信息增益 BaseEntval = calcEnt(data_Y) BestFeature = -1;BestEntGain=0.0 for i in range(fea_num): #开始循环特征 newEntVal = 0.0 #获取每个特征的信息熵 val_nums = np.unique(data_X[:,i]) #先获取该特征下的值种类 for val in val_nums: new_dataY = data_Y[np.where(data_X[:, i] == val)] newEntVal += new_dataY.size/samp_num*calcEnt(new_dataY) if BaseEntval - newEntVal > BestEntGain: #比较信息增益大小 BestEntGain = BaseEntval - newEntVal BestFeature = i return BestFeature #按特征和特征的值进行子集划分 注意:最后返回的子集中不包含原来的特征 def splitDataByFeature(data_X,data_Y,fea_idx,fea_axis,fea_val): #注意fea_idx保存了特征原始索引 new_dataX = data_X[np.where(data_X[:,fea_axis]==fea_val)] new_dataY = data_Y[np.where(data_X[:, fea_axis] == fea_val)] new_dataX = np.delete(new_dataX,fea_axis,1) #按列删除特征 new_feaIdx = np.delete(fea_idx,fea_axis,0) #按行删除 (2,) return new_dataX,new_dataY,new_feaIdx #因为先获取了new_dataY,之后才删除的该特征列,所以必然存在new_dataX为空,new_dataY不为空情况 #开始递归创建树 def createTree(data_X,data_Y,fea_idx): y_valNums = np.unique(data_Y) #值去重 if y_valNums.size == 1: #全是一个类别,直接返回该类别 return np.int(data_Y[0]) if data_X.shape[1] == 0: #如果该递归路径下,已经遍历了所有特征,使用多数投票进行分类返回(这里和splitDataByFeature有关) bestCls,bestCnt = 0,0 for i in y_valNums: if data_Y[np.where(data_Y==i)].size > bestCnt: bestCls = i return bestCls #可以进行递归了 BestFeature = chooseBestFeature(data_X,data_Y) my_tree = {fea_idx[BestFeature]:{}} uniFeaVals = np.unique(data_X[:,BestFeature]) for i in uniFeaVals: new_dataX,new_dataY,new_feaIdx = splitDataByFeature(data_X,data_Y,fea_idx,BestFeature,i) #获取新的划分子集,注意,因为我们是先获取Y标签,然后才删除X矩阵该特征列。所以会出现data_X为空,data_Y不为空情况 my_tree[fea_idx[BestFeature]][i] = createTree(new_dataX,new_dataY,new_feaIdx) return my_tree def classify(inputTree,testVec): #递归查找树,直到找到叶子节点 rootTag = list(inputTree.keys())[0] #获取根节点信息,看先找的哪一个特征 --- 获取索引 FeaVal = inputTree[rootTag] #获取该根节点全部特性值 --- 获取值 for k in FeaVal.keys(): if k == testVec[rootTag]: if type(inputTree[rootTag][k]) != dict: return inputTree[rootTag][k] return classify(inputTree[rootTag][k],testVec) data_x,data_y,fea_names = createDataSet() fea_Idx = np.arange(len(fea_names)) data_X,data_Y = np.array(data_x),np.array([data_y]).T myTree = createTree(data_X,data_Y,fea_Idx) print(myTree) testData = np.zeros(len(fea_names)) for i in range(len(fea_names)): testData[i] = input("{}(0/1)>:".format(fea_names[i])) print(classify(myTree,testData))
二:实现决策树存储
因为构建决策树十分耗时,因此我们希望尽可能少的构建决策树,所以我们把每次构建的决策树存储,在使用的时候进行读取即可,不需要重复进行构建。
import pickle
def storeTree(inputTree,filename): fw = open(filename,"wb") pickle.dump(inputTree,fw) fw.close() def getTree(filename): fr = open(filename,"rb") return pickle.load(fr)
data_x,data_y,fea_names = createDataSet() fea_Idx = np.arange(len(fea_names)) data_X,data_Y = np.array(data_x),np.array([data_y]).T myTree = createTree(data_X,data_Y,fea_Idx) print(myTree) storeTree(myTree,"mytreeStorage.txt") myTree = getTree("mytreeStorage.txt") testData = np.zeros(len(fea_names)) for i in range(len(fea_names)): testData[i] = input("{}(0/1)>:".format(fea_names[i])) print(classify(myTree,testData))
三:案例---预测隐形眼镜类型
(一)代码实现数据预处理---使用pandas读取字符串格式文件转换为可处理数字文件
def preDealData(filename):
df = pd.read_table(filename,'\t',header = None)
columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460
#数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818
new_df = pd.DataFrame()
for i in range(len(columns)):
new_df[i] = pd.factorize(df[i])[0] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。
data_X = new_df.values
data_Y = pd.factorize(df[df.shape[1]-1])[0] #factorize返回的是ndarray类型
data_Y = np.array([data_Y]).T
return data_X,data_Y,columns
(二)全部代码

import numpy as np from math import log import pandas as pd import pickle # 创建数据集 def createDataSet(): dataSet = [[1, 1], [1, 1], [1, 0], [0, 1], [0, 1]] labels = [1, 1, 0, 0, 0] features_names = ['水下', '脚蹼'] # 特征名称 return dataSet, labels, features_names #计算信息熵 def calcEnt(data_Y): #传入numpy数据 cnt = len(data_Y) EntVal = 0.0 val_nums = np.unique(data_Y) for val in val_nums: num = data_Y[np.where(data_Y==val)].size EntVal += num/cnt*log(num/cnt,2) return -EntVal #根据信息熵,获取最好的特征 def chooseBestFeature(data_X,data_Y): samp_num,fea_num = data_X.shape #统计样本数、特征数 #循环统计每个特征的信息增益 BaseEntval = calcEnt(data_Y) BestFeature = -1;BestEntGain=0.0 for i in range(fea_num): #开始循环特征 newEntVal = 0.0 #获取每个特征的信息熵 val_nums = np.unique(data_X[:,i]) #先获取该特征下的值种类 for val in val_nums: new_dataY = data_Y[np.where(data_X[:, i] == val)] newEntVal += new_dataY.size/samp_num*calcEnt(new_dataY) if BaseEntval - newEntVal > BestEntGain: #比较信息增益大小 BestEntGain = BaseEntval - newEntVal BestFeature = i return BestFeature #按特征和特征的值进行子集划分 注意:最后返回的子集中不包含原来的特征 def splitDataByFeature(data_X,data_Y,fea_idx,fea_axis,fea_val): #注意fea_idx保存了特征原始索引 new_dataX = data_X[np.where(data_X[:,fea_axis]==fea_val)] new_dataY = data_Y[np.where(data_X[:, fea_axis] == fea_val)] new_dataX = np.delete(new_dataX,fea_axis,1) #按列删除特征 new_feaIdx = np.delete(fea_idx,fea_axis,0) #按行删除 (2,) return new_dataX,new_dataY,new_feaIdx #因为先获取了new_dataY,之后才删除的该特征列,所以必然存在new_dataX为空,new_dataY不为空情况 #开始递归创建树 def createTree(data_X,data_Y,fea_idx): y_valNums = np.unique(data_Y) #值去重 if y_valNums.size == 1: #全是一个类别,直接返回该类别 return data_Y[0] # return np.int(data_Y[0]) if data_X.shape[1] == 0: #如果该递归路径下,已经遍历了所有特征,使用多数投票进行分类返回(这里和splitDataByFeature有关) bestCls,bestCnt = 0,0 for i in y_valNums: if data_Y[np.where(data_Y==i)].size > bestCnt: bestCls = i return bestCls #可以进行递归了 BestFeature = chooseBestFeature(data_X,data_Y) my_tree = {fea_idx[BestFeature]:{}} uniFeaVals = np.unique(data_X[:,BestFeature]) for i in uniFeaVals: new_dataX,new_dataY,new_feaIdx = splitDataByFeature(data_X,data_Y,fea_idx,BestFeature,i) #获取新的划分子集,注意,因为我们是先获取Y标签,然后才删除X矩阵该特征列。所以会出现data_X为空,data_Y不为空情况 my_tree[fea_idx[BestFeature]][i] = createTree(new_dataX,new_dataY,new_feaIdx) return my_tree def classify(inputTree,testVec): #递归查找树,直到找到叶子节点 rootTag = list(inputTree.keys())[0] #获取根节点信息,看先找的哪一个特征 --- 获取索引 FeaVal = inputTree[rootTag] #获取该根节点全部特性值 --- 获取值 for k in FeaVal.keys(): if k == testVec[rootTag]: if type(inputTree[rootTag][k]) != dict: return inputTree[rootTag][k] return classify(inputTree[rootTag][k],testVec) def storeTree(inputTree,filename): fw = open(filename,"wb") pickle.dump(inputTree,fw) fw.close() def getTree(filename): fr = open(filename,"rb") return pickle.load(fr) def preDealData(filename): df = pd.read_table(filename,'\t',header = None) columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460 #数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818 new_df = pd.DataFrame() for i in range(len(columns)): new_df[i] = pd.factorize(df[i])[0] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。 data_X = new_df.values data_Y = pd.factorize(df[df.shape[1]-1])[0] #factorize返回的是ndarray类型 data_Y = np.array([data_Y]).T return data_X,data_Y,columns data_X,data_Y,fea_names = preDealData("lenses.txt") fea_Idx = np.arange(len(fea_names)) myTree = createTree(data_X,data_Y,fea_Idx) print(myTree)
(三)结果展示
{3: {
0: array([0], dtype=int64),
1: {
2: {
0: {
0: {
0: array([1], dtype=int64),
1: array([1], dtype=int64),
2: {
1: {
0: array([0], dtype=int64),
1: array([1], dtype=int64)
}
}
}
},
1: {
1: {
0: array([2], dtype=int64),
1: {
0: {
0: array([2], dtype=int64),
1: array([0], dtype=int64),
2: array([0], dtype=int64)
}
}
}
}
}
}
}
}
变形为:
["age","prescript","astigmatic","tearRate"]
{tearRate: { reduced: array([0], dtype=int64), normal:{ astigmatic: { no: { age: { young: array([1], dtype=int64), ---> soft pre: array([1], dtype=int64), ---> soft presbyopic: { prescript: { myope: array([0], dtype=int64), ---> no lenses hyper: array([1], dtype=int64) ---> soft } } } }, yes: { prescript: { myope: array([2], dtype=int64), ---> hard hyper: { age: { young: array([2], dtype=int64), ---> hard pre: array([0], dtype=int64), ---> no lenses presbyopic: array([0], dtype=int64) ---> no lenses } } } } } } } }
作者:山上有风景
欢迎任何形式的转载,但请务必注明出处。
限于本人水平,如果文章和代码有表述不当之处,还请不吝赐教。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
2018-07-03 OpenCV---ROI(region of interest)和泛洪填充
2018-07-03 OpenCV---像素运算
2018-07-03 OpenCV---色彩空间(二)HSV追踪颜色对象和通道分离与合并
2018-07-03 OpenCV---色彩空间(一)
2018-07-03 OpenCV---Numpy数组的使用以及创建图片