统计学习方法---K-近邻（kd树实现）
https://blog.csdn.net/App_12062011/article/details/51986805
一：kd树构建
以二维平面点((x,y))的集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)为例结合下图来说明k-d tree的构建过程。
（一）构建步骤
1.构建根节点时，此时的切分维度为(x)，如上点集合在(x)维从小到大排序为：
(2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)；
其中中位数为7，选择中值(7,2)。（注：2,4,5,7,8,9在数学中的中值为(5 + 7)/2=6，但因该算法的中值需在点集合之内，所以本文中值计算用的是len(points)//2=3, points[3]=(7,2)）
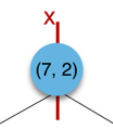
2.(2,3)，(4,7)，(5,4)挂在(7,2)节点的左子树，(8,1)，(9,6)挂在(7,2)节点的右子树。
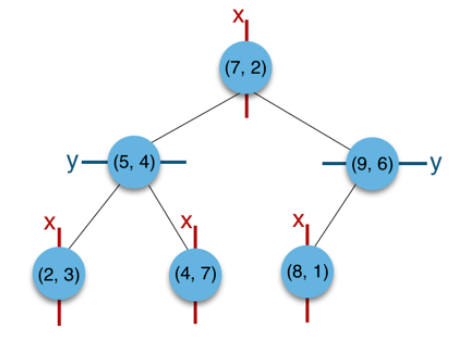
3.构建(7,2)节点的左子树时，点集合(2,3)，(4,7)，(5,4)此时的切分维度为(y)，从3，4，7选取中位数4，中值为(5,4)作为分割平面，(2,3)挂在其左子树，(4,7)挂在其右子树。
4.构建(7,2)节点的右子树时，点集合(8,1)，(9,6)此时的切分维度也为(y)，中值为(9,6)作为分割平面，(8,1)挂在其左子树。至此k-d tree构建完成。
上述的构建过程结合下图可以看出，构建一个k-d tree即是将一个二维平面逐步划分的过程。
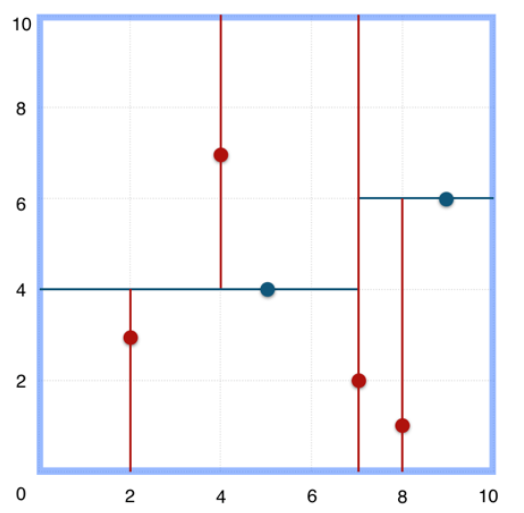
（二）代码实现构建kd树
class Node: def __init__(self,data,sp=0,left=None,right=None): self.data = data self.sp = sp #0是按特征1排序，1是按特征2排序 self.left = left self.right = right def __lt__(self, other): return self.data < other.data
class KDTree: def __init__(self,data): self.dim = data.shape[1] self.root = self.createTree(data,0) self.nearest_node = None self.nearest_dist = np.inf #设置无穷大 def createTree(self,dataset,sp): if len(dataset) == 0: return None dataset_sorted = dataset[np.argsort(dataset[:,sp])] #按特征列进行排序 #获取中位数索引 mid = len(dataset) // 2 #生成节点 left = self.createTree(dataset_sorted[:mid],(sp+1)%self.dim) right = self.createTree(dataset_sorted[mid+1:],(sp+1)%self.dim) parentNode = Node(dataset_sorted[mid],sp,left,right) return parentNode
data = np.array([[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]) kdtree = KDTree(data) #创建KDTree
二：kd树搜索（找最近邻节点）
注意：最近邻---当k为1时，称为最近邻。
在k-d树中进行数据的查找也是特征匹配的重要环节，其目的是检索在k-d树中与查询点距离最近的数据点。
（一）简单案例一：查询的点（2.1,3.1）
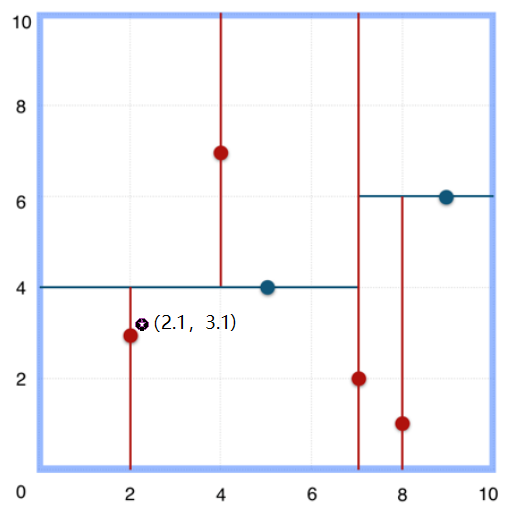
1.通过二叉搜索，从根节点顺着搜索路径很快就能找到最邻近的近似点，也就是叶子节点（2,3）。
2.而找到的叶子节点并不一定就是最邻近的，最邻近肯定距离查询点更近，应该位于以查询点为圆心且通过叶子节点的圆域内。
3.为了找到真正的最近邻，还需要进行'回溯'操作：
算法沿搜索路径反向查找是否有距离查询点更近的数据点。
推导：
1.此例中先从（7,2）点开始进行二叉查找，然后到达（5,4），最后到达（2,3），此时搜索路径中的节点为<（7,2），（5,4），（2,3）>。
2.首先以（2,3）作为当前最近邻点，计算其到查询点（2.1,3.1）的距离为0.1414，
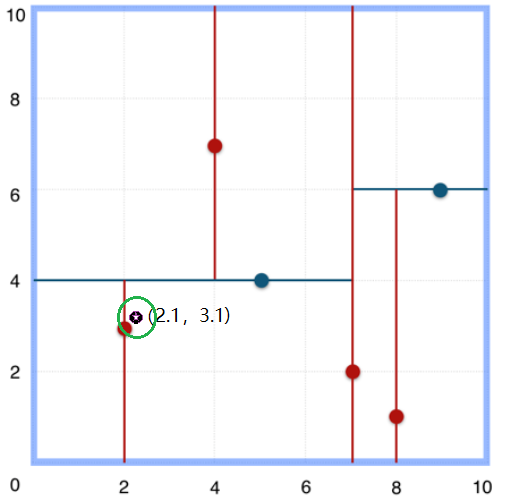
3.然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如图3所示。发现该圆并不和超平面y = 4交割，因此不用进入（5,4）节点右子空间中去搜索。
4.4、最后，再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。
（二）案例二：查找点为（2，4.5）
1.同样先进行二叉查找，先从（7,2）查找到（5,4）节点，在进行查找时是由y = 4为分割超平面的，由于查找点为y值为4.5，因此进入右子空间查找到（4,7），形成搜索路径<（7,2），（5,4），（4,7）>
2.取（4,7）为当前最近邻点，计算其与目标查找点的距离为3.202。
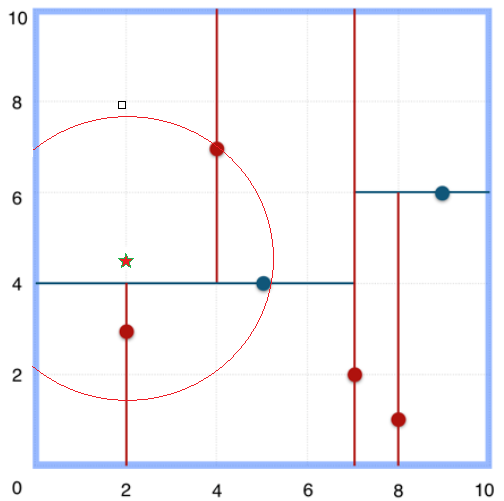
3.然后回溯到（5,4），计算其与查找点之间的距离为3.041。（（4,7）与目标查找点的距离为3.202，而（5,4）与查找点之间的距离为3.041，所以（5,4）为查询点的最近点；）
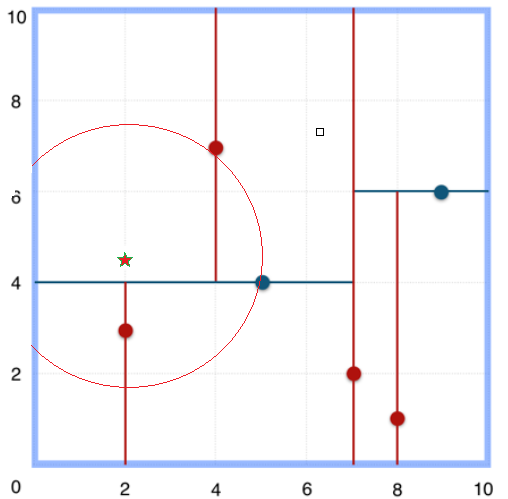
4.以（2，4.5）为圆心，以3.041为半径作圆，如图4所示。可见该圆和y = 4超平面交割，所以需要进入（5,4）左子空间进行查找。此时需将（2,3）节点加入搜索路径中得<（7,2），（2,3）>。
5.回溯至（2,3）叶子节点，（2,3）距离（2,4.5）比（5,4）要近，所以最近邻点更新为（2，3），最近距离更新为1.5。
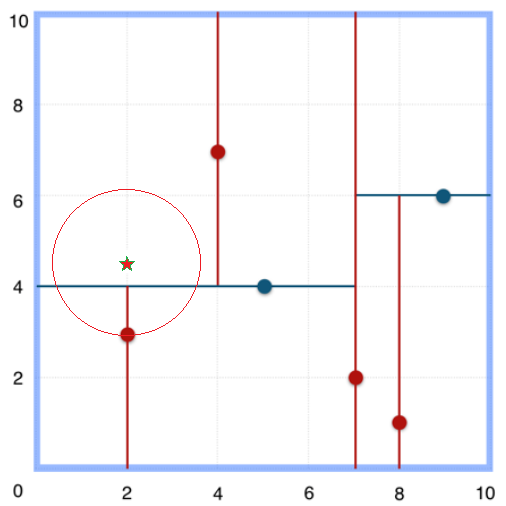
6.回溯至（7,2），以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割。
至此，搜索路径回溯完。返回最近邻点（2,3），最近距离1.5。
（三）代码实现
import numpy as np class Node: def __init__(self,data,sp=0,left=None,right=None): self.data = data self.sp = sp #0是按特征1排序，1是按特征2排序 self.left = left self.right = right def __lt__(self, other): return self.data < other.data
class KDTree: def __init__(self,data): self.dim = data.shape[1] self.root = self.createTree(data,0) self.nearest_node = None self.nearest_dist = np.inf #设置无穷大 def createTree(self,dataset,sp): if len(dataset) == 0: return None dataset_sorted = dataset[np.argsort(dataset[:,sp])] #按特征列进行排序 #获取中位数索引 mid = len(dataset) // 2 #生成节点 left = self.createTree(dataset_sorted[:mid],(sp+1)%self.dim) right = self.createTree(dataset_sorted[mid+1:],(sp+1)%self.dim) parentNode = Node(dataset_sorted[mid],sp,left,right) return parentNode def nearest(self, x): def visit(node): if node != None: dis = node.data[node.sp] - x[node.sp] #访问子节点 visit(node.left if dis > 0 else node.right) #查看当前节点到目标节点的距离 二范数求距离 curr_dis = np.linalg.norm(x-node.data,2) #更新节点 if curr_dis < self.nearest_dist: self.nearest_dist = curr_dis self.nearest_node = node #比较目标节点到当前节点距离是否超过当前超平面，超过了就需要到另一个子树中 if self.nearest_dist > abs(dis): #要到另一面查找 所以判断条件与上面相反 visit(node.left if dis < 0 else node.right) #从根节点开始查找 node = self.root visit(node) return self.nearest_node.data,self.nearest_dist
data = np.array([[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]) kdtree = KDTree(data) #创建KDTree node,dist = kdtree.nearest(np.array([6,5])) print(node,dist)
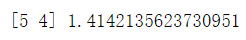
（四）性能对比
https://www.cnblogs.com/21207-ihome/p/6084670.html
一般来讲，最临近搜索只需要检测几个叶子结点即可，如下图所示：
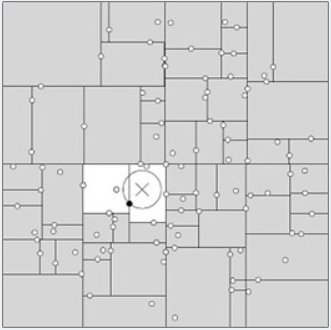
但是，如果当实例点的分布比较糟糕时，几乎要遍历所有的结点，如下所示：
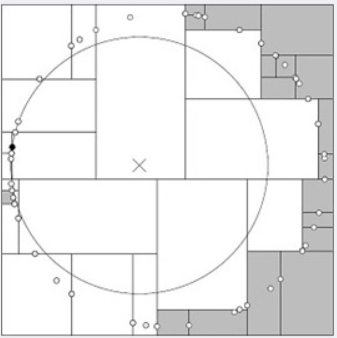
三：K-近邻算法中kd树搜索最近K个节点
补充：python内部没有实现大顶堆，应该如何处理？
将原来得x值，变为-x即可
（一）算法思路（借助堆排序---heapq）
我们借助大小为k得大顶堆来实现我们K-近邻算法：
1.首先，从根节点向下查找到叶节点
2.从叶节点开始回溯，记录每一个距离目标点的距离到最大堆中。
（1）如果堆的大小<k，则正常回溯，并且如果到了根节点，我们也要去访问另一侧子树
（2）如果堆的大小=k,我们每一次回溯时取出最大值，查看目标点是否与当前节点的另一侧相交，然后决定是否去访问另一侧。当获取的新的节点距离目标节点更小，则将当前最大距离出堆，将当前值插入，重新排序。直到我们找到的k个元素中的最大值，不再与当前节点另一边相交即可。
（二）代码实现
import numpy as np import heapq class Node: def __init__(self,data,sp=0,left=None,right=None): self.data = data self.sp = sp #0是按特征1排序，1是按特征2排序 self.left = left self.right = right self.nearest_dist = -np.inf #我们需要使用最小堆来模拟最大堆，我们设置默认大小-∞，实际就是+∞ def __lt__(self, other): return self.nearest_dist < other.nearest_dist class KDTree: def __init__(self,data): self.k = data.shape[1] self.root = self.createTree(data,0) self.heap = [] #初始化一个堆 def createTree(self,dataset,sp): if len(dataset) == 0: return None dataset_sorted = dataset[np.argsort(dataset[:,sp])] #按特征列进行排序 #获取中位数索引 mid = len(dataset) // 2 #生成节点 left = self.createTree(dataset_sorted[:mid],(sp+1)%self.k) right = self.createTree(dataset_sorted[mid+1:],(sp+1)%self.k) parentNode = Node(dataset_sorted[mid],sp,left,right) return parentNode def nearest(self, x, k): def visit(node): if node != None: dis = node.data[node.sp] - x[node.sp] #访问子节点 visit(node.left if dis > 0 else node.right) #查看当前节点到目标节点的距离 二范数求距离 curr_dis = np.linalg.norm(x-node.data,2) node.nearest_dist = -curr_dis #更新节点 if len(self.heap) < k: #直接加入 heapq.heappush(self.heap,node) else: #先获取最大堆最大值，比较后决定 if nsmallest(1,self.heap)[0].nearest_dist < -curr_dis: heapq.heapreplace(self.heap, node) #比较目标节点到当前节点距离是否超过当前超平面，超过了就需要到另一个子树中 if len(self.heap) < k or abs(nsmallest(1,self.heap)[0].nearest_dist) > abs(dis): #要到另一面查找 所以判断条件与上面相反 visit(node.left if dis < 0 else node.right) #从根节点开始查找 node = self.root visit(node) nds = nlargest(k,self.heap) for i in range(k): nd = nds[i] print(nd.data,nd.nearest_dist)
data = np.array([[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]) kdtree = KDTree(data) #创建KDTree kdtree.nearest(np.array([6,5]),5)
（三）对比原始KNN
import numpy as np import matplotlib.pyplot as plt import pandas as pd def KNNClassfy(preData,dataSet,k): distance = np.sum(np.power(dataSet - preData,2),1) #注意：这里我们不进行开方，可以少算一次 sortDistIdx = np.argsort(distance,0)[:k] #小到大排序，获取索引 for i in range(k): print(dataSet[sortDistIdx[i]],np.linalg.norm(dataSet[sortDistIdx[i]]-preData,2)) data = np.array([[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]) predata = np.array([6,5]) KNNClassfy(predata,data,5)
