机器学习作业---推荐系统
-------------------------------实现协同过滤学习算法-------------------------------
实现协同过滤学习算法,并将其应用于电影评级数据集。这个数据集由1到5的等级组成。数据集有nu = 943个用户,nm = 1682个电影
一:导入数据及可视化
(一)导入数据
data = sio.loadmat("ex8_movies.mat")

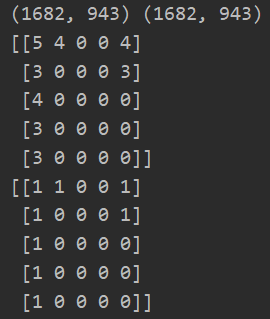
Y = data['Y'] R = data['R'] print(Y.shape,R.shape) #(1682, 943) (1682, 943) print(Y[:5,:5]) #Y表示了用户对电影的评分(0-5),但是其中有些评价是0分,有些并没有评价,但是也是显示0.所以需要下面的矩阵来区分是否被评价 print(R[:5,:5]) #R表示了用户是否对某个电影评价,0表示没有评价,1表示评价了
#第一部电影《玩具总动员》的平均得分(所有评过分的平均值) mu = np.mean(Y[0,np.where(R[0,:]==1)]) print(mu)

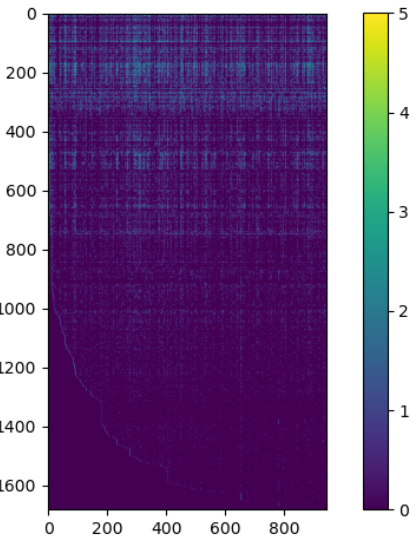
(二)可视化电影评价矩阵图
plt.figure()
plt.imshow(Y)
plt.colorbar()
plt.show()
二:协同过滤代价函数
(一)导入数据(提供给我们的随机初始化过的参数)
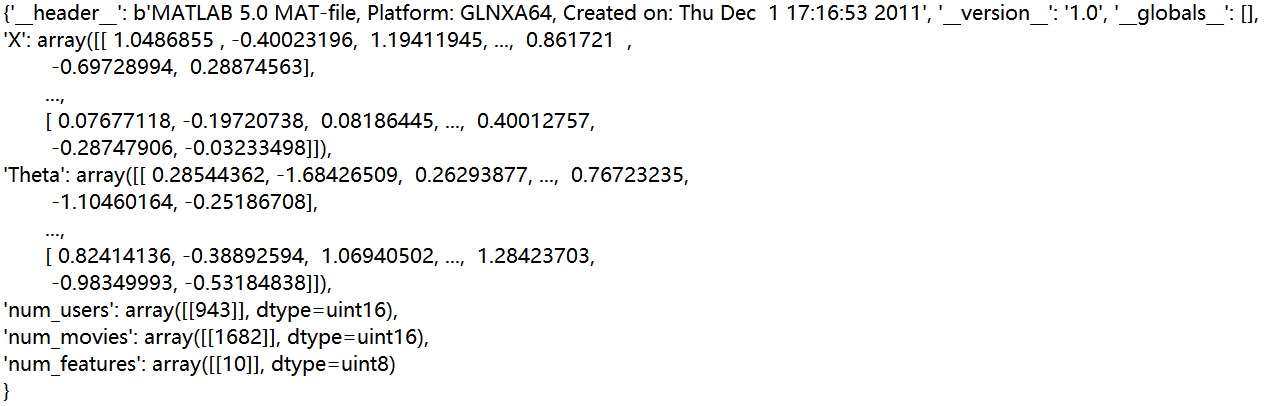
#导入我们已经初始化的参数 params = sio.loadmat("ex8_movieParams.mat") print(params)
#导入我们已经初始化的参数
params = sio.loadmat("ex8_movieParams.mat")
X = params['X'] #获取电影的特征矩阵
theta = params['Theta'] #获取用户的特征矩阵
# print(X.shape,theta.shape) #(1682, 10) (943, 10)
num_users = params['num_users'] #获取用户数943
num_movies = params['num_movies'] #获取电影数1682
num_features = params['num_features'] #获取电影、用户特征数10
(二)减少数据集,用于提高测试速度
#减小数据集用来更快的测试代价函数的正确性 num_users = 4 num_movies = 5 num_features = 3 X = X[0:num_movies,0:num_features] theta = theta[0:num_users,0:num_features] Y = Y[0:num_movies,0:num_users] R = R[0:num_movies,0:num_users]
(三)实现协同过滤代价函数(含正则项)
无正则化协同过滤代价函数公式:
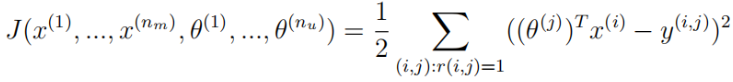
正则化代价函数公式:
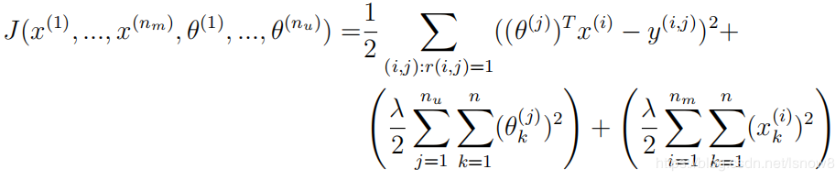
1.代码实现
#注意:我们后面要保持参数和梯度下降一致,而且为了以后可以使用高级优化算法 #我们需要将要拟合的数据全部放在第一个参数中 #因为我们要协同拟合θ和x,所以我们使用params合并X和θ def cofi_cost_function(params,Y,R,num_users,num_movies,num_features,lmd=0): X = params[0:num_movies*num_features].reshape((num_movies,num_features)) theta = params[num_movies*num_features:].reshape((num_users,num_features)) # print(X.shape,theta.shape,Y.shape) #(5, 3) (4, 3) (5, 4) J = np.sum(np.power(X.dot(theta.T)-Y,2)[np.where(R==1)])/2 reg = (lmd/2)*(np.sum(np.power(X,2))+np.sum(np.power(theta,2))) return J + reg
2.代价函数测试
#导入用户和电影评价数据 data = sio.loadmat("ex8_movies.mat") Y = data['Y'] R = data['R'] # print(Y.shape,R.shape) #(1682, 943) (1682, 943) # print(Y[:5,:5]) #Y表示了用户对电影的评分(0-5),但是其中有些评价是0分,有些并没有评价,但是也是显示0.所以需要下面的矩阵来区分是否被评价 # print(R[:5,:5]) #R表示了用户是否对某个电影评价,0表示没有评价,1表示评价了 #导入我们已经训练好的参数 params = sio.loadmat("ex8_movieParams.mat") X = params['X'] #获取电影的特征矩阵 theta = params['Theta'] #获取用户的特征矩阵 # print(X.shape,theta.shape) #(1682, 10) (943, 10) num_users = params['num_users'] #获取用户数943 num_movies = params['num_movies'] #获取电影数1682 num_features = params['num_features'] #获取用户、电影特征数10 #减小数据集用来更快的测试代价函数的正确性 num_users = 4 num_movies = 5 num_features = 3 X = X[0:num_movies,0:num_features] theta = theta[0:num_users,0:num_features] Y = Y[0:num_movies,0:num_users] R = R[0:num_movies,0:num_users] #将参数X和参数theta合并 np.r_是按列合并 params = np.r_[np.array(X.flatten()),np.array(theta.flatten())] J = cofi_cost_function(params,Y,R,num_users,num_movies,num_features) print(J)

三:协同过滤梯度下降函数
(一)梯度下降公式(既要更新未评价电影可能评价以便推荐,又要更新用户的电影评价参数:)
1.无正则化梯度下降公式
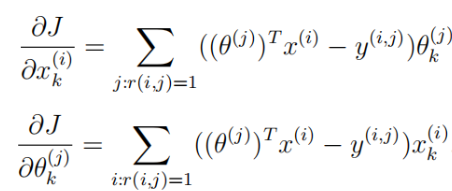
2.正则化梯度下降公式:

(二)代码实现
def cofi_grad_function(params,Y,R,num_users,num_movies,num_features,lmd=0): X = params[0:num_movies*num_features].reshape((num_movies,num_features)) theta = params[num_movies*num_features:].reshape((num_users,num_features)) # print((X.dot(theta.T)-Y).shape,theta.shape,X.shape,R.shape) #(5, 4) (4, 3) (5, 3) (5, 4) X_grad = ((X.dot(theta.T)-Y)*R).dot(theta)+lmd*X theta_grad = ((X.dot(theta.T)-Y)*R).T.dot(X)+lmd*theta # print(X_grad.shape,theta_grad.shape) #(5, 3) (4, 3)求梯度以后,保持维度不变 grad = np.r_[X_grad.flatten(),theta_grad.flatten()] return grad #返回一维数组,大小同参数一致
补充:同型矩阵使用"*"---对应元素相乘
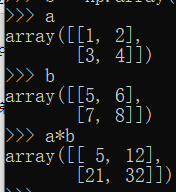
(三)代码测试
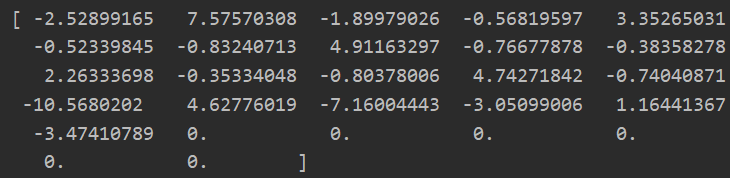
grad = cofi_grad_function(params,Y,R,num_users,num_movies,num_features) print(grad) print(grad.shape)
四:梯度检测(可选)---利用导数定义求解理论上的梯度值
(一)知识回顾
https://www.cnblogs.com/ssyfj/p/12865515.html

上图中,是对一个参数θ进行求偏导,而我们这里是对θ和x一起求偏导。所以我们使得两个变量,变成一个params进行求解偏导。
算法伪代码:

n代表了θ参数维度,我们对每一个θ_i执行上面的求导方法。之后检验我们使用导数定义求得的导数和使用反向传播求得的导数是否接近(几位小数差距)或者相等。那么我们就可以确定反向传播的实现是正确的。可以很好的优化J(θ)
注意:我们只需要使用一次梯度检验来检验我们反向传播算法求得的导数是否正确。如果正确,那么我们后面的学习就需要关闭梯度检验(因为使用梯度检验计算量大、且慢)
注意:简单的梯度检验 利用数值估计的梯度和真实的梯度二范数之差除以二范数值之和就是误差
(二)代码实现定义求解梯度
def computeNumerialGradient(J,params,,Y,R,num_users,num_movies,num_features,lmd=0): def cost_func(params_): #为了方便我们这里求导,将上面的代价函数简写 return cofi_cost_function(params_,Y,R,num_users,num_movies,num_features,lmd) numgrad = np.zeros(params.size) #保存梯度信息 perturb = np.zeros(params.size) #用于保持一个维度的θ_j可以减去ε。其他全为0 e = 1e-4 for i in range(params.size): # 对每一个都求一次导 perturb[i] = e J_1 = cost_func(params-e) J_2 = cost_func(params+e) numgrad[i] = (J_2-J_1)/(2*e) perturb[i] = 0 #还原该位置,我们要保持一次只有一个位置为ε return numgrad
(三)代码实现梯度检验
#求一次梯度情况 #计算数值梯度与理论梯度之间的差值 grad = cofi_grad_function(params,Y,R,num_users,num_movies,num_features) numgrad = computeNumerialGradient(params,Y,R,num_users,num_movies,num_features) diff = np.linalg.norm(numgrad-grad)/np.linalg.norm(numgrad+grad) print(diff)

差值比1e-9小得多,所以几乎一致,检验通过。
(四)测试正则化后的代价函数和梯度函数
lmd = 1.5 #求一次梯度情况 #计算数值梯度与理论梯度之间的差值 grad = cofi_grad_function(params,Y,R,num_users,num_movies,num_features,lmd) numgrad = computeNumerialGradient(params,Y,R,num_users,num_movies,num_features,lmd) diff = np.linalg.norm(numgrad-grad)/np.linalg.norm(numgrad+grad) print(diff)

总结:通过这里的检验,我们可以知道我们实现的梯度下降和代价函数是正确的,下面我们可以使用这两个函数来进行参数拟合!!!
五: 高级优化算法拟合参数,拟合新用户可能对电影的评分,从而进行推荐
(一)由于提供的电影名称数据可能出现编码错误,我们需要先处理一下

![]()
1.找到有问题的行信息
f = open('movie_ids.txt',"rb")#二进制格式读文件 lines = f.readlines() for line in lines: try: line.decode('utf8') #解码 except: #打印编码有问题的行 print(str(line)) f.close
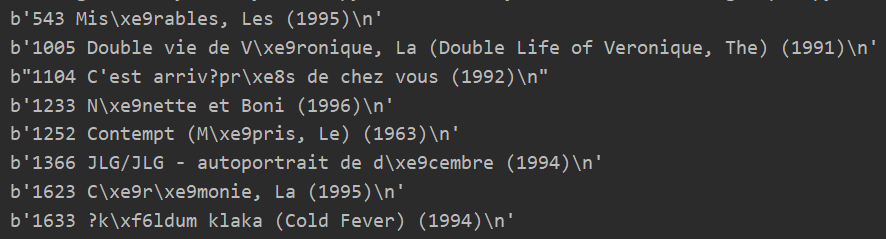
主要就是ö、é、è这几个字符,替换成o、e即可
2.手动修改一下该文件
3.获取电影名称信息
movies_list = [] f = open('movie_ids.txt',"r")#二进制格式读文件 lines = f.readlines() for line in lines: line = line.split("\n")[0] movies_list.append(" ".join(line.split(" ")[1:])) f.close print(movies_list)

(二)初始化新用户评分
num_users = np.int(params['num_users']) #获取用户数943 num_movies = np.int(params['num_movies']) #获取电影数1682 num_features = np.int(params['num_features']) #获取用户、电影特征数10 X = X[0:num_movies,0:num_features] theta = theta[0:num_users,0:num_features] Y = Y[0:num_movies,0:num_users] R = R[0:num_movies,0:num_users] #将参数X和参数theta合并 np.r_是按列合并 params = np.r_[np.array(X.flatten()),np.array(theta.flatten())] movies_list = [] f = open('movie_ids.txt',"r")#二进制格式读文件 lines = f.readlines() for line in lines: line = line.split("\n")[0] movies_list.append(" ".join(line.split(" ")[1:])) f.close #初始化新用户信息(该用户只评价了部分电影) my_ratings = np.zeros((num_movies,1)) #该用户评价了少数电影 my_ratings[0] = 4 my_ratings[97] = 2 my_ratings[6] = 3 my_ratings[11] = 5 my_ratings[53] = 4 my_ratings[63] = 5 my_ratings[65] = 3 my_ratings[68] = 5 my_ratings[182] = 4 my_ratings[225] = 5 my_ratings[354] = 5 #我们查看他评价的电影及给的评分 for i in range(num_movies): if my_ratings[i] > 0: print("Rated %d for %s"%(my_ratings[i],movies_list[i]))

(三)将新用户的信息合并到原始评分矩阵中去
Y = np.c_[my_ratings,Y]
R = np.c_[np.where(my_ratings!=0,1,0),R]
# print(Y.shape,R.shape)
#更新用户、电影特征(其实也不是更新,我们前面提供的参数,到后面我们会自己实现一份随机初始化的参数,所以后面不会遇到前面的params)
num_users = Y.shape[1] #获取用户数944
num_movies = Y.shape[0] #获取电影数1682
num_features = 10 #这里更新特征
(四)均值规范化
如果考虑这样的例子,有一个用户没有给任何电影评分,那么均值规范化对算法的实现会更加友好!!!
因为如果出现没有给任何电影评分,会导致无论如何学习,但是这样预测的结果都为0,显然不是我们想要的结果,接下来将用均值归一化的思想来解决这个问题。(具体讲解看https://www.cnblogs.com/ssyfj/p/12951542.html)
对用户来说,由于之前没有给电影进行评分,学习到的参数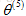
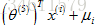
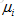
def mean_normalization(Y,R): mu = (np.sum(Y,axis=1)/np.sum(R,axis=1)).reshape(-1,1) #求行均值,注意将(1682,)变为(1682,1) Y_ = (Y - mu)*R #对于没有评分的,评分还是0 return mu,Y_
Y_mu,Y_norm = mean_normalization(Y,R)
(五)随机初始化参数列表(我们就不需要二中提供的参数了)
X = np.random.randn(num_movies,num_features) #初始化电影的特征矩阵 theta = np.random.randn(num_users,num_features) #初始化用户的特征矩阵 #将参数X和参数theta合并 np.r_是按列合并 params = np.r_[np.array(X.flatten()),np.array(theta.flatten())]
(六)使用高级优化算法拟合参数
lmd = 10 #使用高级优化算法,拟合参数 res = opt.minimize(fun=cofi_cost_function,x0=params, args=(Y_norm,R,num_users,num_movies,num_features,lmd), method="TNC",jac=cofi_grad_function,options={"maxiter":100}) #得到模型参数 params = res.x X = params[0:num_movies * num_features].reshape((num_movies, num_features)) theta = params[num_movies * num_features:].reshape((num_users, num_features))
print(X.shape,theta.shape)

(七)预测评分矩阵
#预测评分矩阵 p = X @ theta.T print(p[:,0].shape) my_predictions = (p[:,0].reshape(Y_mu.shape)+Y_mu).flatten() #使得和均值相加,到这里才完成全部的均值规范化 print(my_predictions)
![]()

预测波动范围在(0.99-5.0)之间
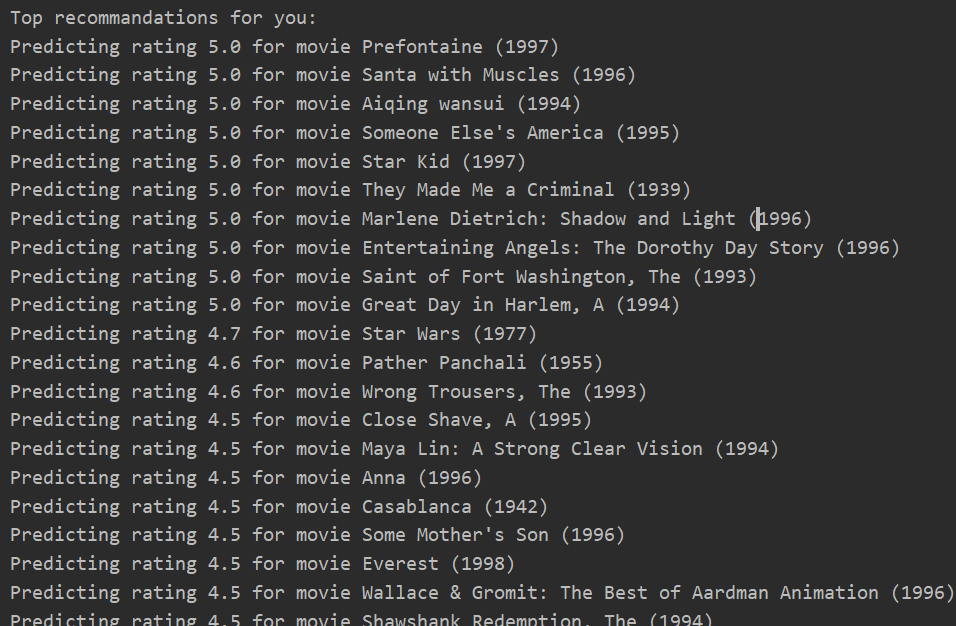
(八)推荐电影(注意:由于随机初始化问题,可能推荐结果不一致)
#推荐100部,我们最可能喜欢的电影 #先将我们的电影预测评分大到小排序 predictions = np.argsort(my_predictions)[::-1] #逆序排序,大到小 print("Top recommandations for you:") for i in range(100): j = predictions[i] #获取电影索引号 print("Predicting rating %.1f for movie %s"%(my_predictions[j],movies_list[j]))