机器学习作业---异常检测
一：异常检测回顾
异常检测也是一个无监督学习算法
（一）异常检测做什么？
从一组数据中找到那些“异常”的数据，基于高斯分布（正态分布）。
生活中的很多事情都是符合高斯分布的，对于数据也是如此。
我们通过参数估计，估计出数据符合的高斯分布参数，当其中的数据分布在高斯分布中概率很小的地方，就认为这是异常数据。
（二）具体怎么做？
选择那些你认为处于异常状态（有反常样本）的特征xj作为输入：（下面是该xj特征的样本）
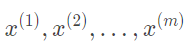
根据上面每个特征的样本数据估计高斯分布的参数(对每一个特征)
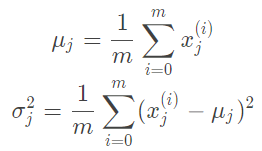
对于一个新的数据，预测其发生概率
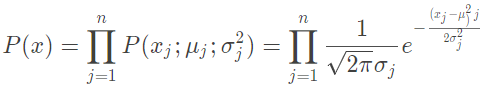
当概率小于一定阈值后认定为异常。
（三）这个算法有什么缺点？
可以看到，之前的模型中对每个特征都是独立地处理，最后的组合只是简单的相乘。这样就是存在一些问题，特征之间的关联没有捕捉到。
升级的方式就是多元高斯分布，将不再单独考虑特征，而是将特征一起考虑，自动捕捉之间的关联。
参数的估计变为，其中的sigma为协方差矩阵：
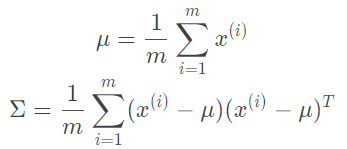
预测变为：
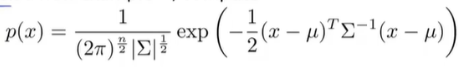
这个模型有个前提就是m>n，而且协方差矩阵是非奇异矩阵。另外这个计算也是复杂的。
（四）怎么评估算法的效果？
使用标签化的数据，计算F1score：
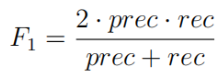
查准率和查全率公式：
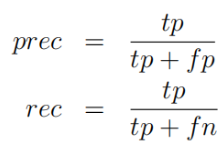
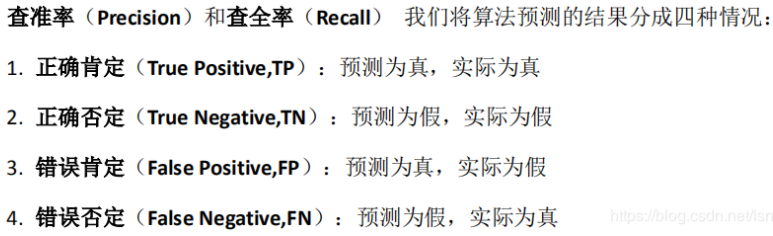
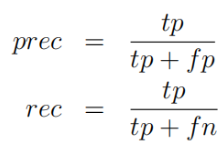
二：作业介绍
在本练习中，将实现一个异常检测算法来检测服务器计算机中的异常行为。这些特性度量每个服务器的吞吐量(mb/s)和响应延迟(ms)。在您的服务器运行时，您收集了m = 307个关于它们行为的示例，因此有一个未标记的dataset {x(1)，…，x(m)}。您怀疑这些示例中的绝大多数都是服务器正常运行的“正常”(非异常)示例，但是也可能有一些服务器在这个数据集中异常运行的示例。
将使用高斯模型来检测数据集中的异常示例。您将首先从一个2D数据集开始，该数据集将允许您可视化算法在做什么。在该数据集上，将拟合高斯分布，然后找到概率非常低的值，因此可以考虑异常。之后，您将把异常检测算法应用于具有多个维度的较大数据集
三：数据导入及可视化
import numpy as np import matplotlib.pyplot as plt import scipy.io as sio data = sio.loadmat("ex8data1.mat") X = data['X'] Xval = data['Xval'] #获取验证集 yval = data['yval'].flatten() print(X.shape) print(Xval.shape,yval.shape) plt.figure() plt.scatter(X[:,0],X[:,1],c='b',marker='x',s=15,linewidths=1) plt.show()
四：估计高斯分布的参数(对每一个特征)均值和方差
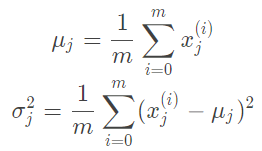
def estimate_gussian(X): mu = np.mean(X,0) sigma2 = np.sum(np.power(X-mu,2),0)/X.shape[0] return mu,sigma2
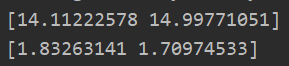
data = sio.loadmat("ex8data1.mat") X = data['X'] Xval = data['Xval'] #获取验证集 yval = data['yval'].flatten() mu,sigma2 = estimate_gussian(X) print(mu) print(sigma2)
五：实现高斯分布模型
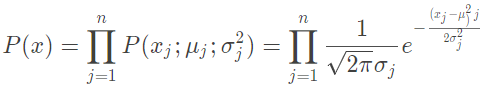
def gaussian_distribution(X,mu,sigma2): p = (1/np.sqrt(2*np.pi*sigma2))*np.exp(-np.power((X-mu),2)/(2*sigma2)) return np.prod(p,axis=1) #横向累乘
px = gaussian_distribution(X,mu,sigma2) print(px.shape) print(px[:10])
六：绘制轮廓线，进行可视化
def visualize_countours(mu,sigma2): #绘制高斯分布等高线 #由上图可以知道，我们选取5-25，范围比较合适 x = np.linspace(5,25,100) y = np.linspace(5,25,100) xx,yy =np.meshgrid(x,y) X = np.c_[xx.flatten(),yy.flatten()] #数据对应网格中每一个点 z = gaussian_distribution(X,mu,sigma2).reshape(xx.shape) #获取每一个点坐标的高斯值 cont_levels = [10 ** h for h in range(-20, 0, 3)] #当z为当前列表的值才绘出等高线（最高1） 不设置的话，会比较奇怪 plt.contour(xx,yy,z,cont_levels)
data = sio.loadmat("ex8data1.mat") X = data['X'] Xval = data['Xval'] #获取验证集 yval = data['yval'].flatten() mu,sigma2 = estimate_gussian(X) px = gaussian_distribution(X,mu,sigma2) plt.figure() visualize_countours(mu,sigma2) plt.scatter(X[:,0],X[:,1],c='b',marker='x',s=15,linewidths=1) plt.show()
七：选择阈值
取最好的F1分数及对应的阈值进行返回
计算F1score：
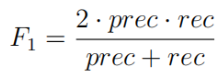
查准率和查全率公式：
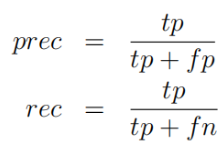
def select_threshold(yval,pval): #yval是验证集标签 0或者1，pval是我们进行高斯处理后得到的概率在[0,1]之间 best_eps = 0 best_f1 = 0 for epsilon in np.linspace(np.min(pval),np.max(pval),num=1001): predictions = np.where(pval < epsilon, 1, 0) # 小于epsilon则预测为异常(为真） 满足条件返回1，不满足返回0 tp = np.sum(yval[np.where(predictions==1)]) #正确肯定 上面预测的为1，并且yval中也是1，我们才进行添加 fp = np.sum(np.where(yval[np.where(predictions==1)]==0,1,0)) #错误肯定 预测为真，实际为假 fn = np.sum(np.where(yval[np.where(predictions==0)]==1,1,0)) #错误否定 #计算查准率和查全率 if tp+fp == 0 or tp + fn ==0: continue prec = tp / (tp + fp) # 查准率 rec = tp / (tp + fn) # 查全率 #计算F1-score f1 = 2*prec*rec/(prec+rec) if f1 > best_f1: best_f1 = f1 best_eps = epsilon return best_eps,best_f1
mu,sigma2 = estimate_gussian(X) #利用训练集获取均值方差
px = gaussian_distribution(Xval,mu,sigma2) #利用验证集数据，获取高斯概率
eps,f1 = select_threshold(yval,px) #利用验证集标签进行判断，获取阈值
print(eps,f1)
八：根据阈值来判断异常
def detection(X,eps,mu,sigma2): px = gaussian_distribution(X,mu,sigma2) #获取训练集的高斯分布值 #进行判断异常点 anomaly_points = X[np.where(px<eps)] return anomaly_points
def circle_anomaly_points(X): #将异常点圈出 plt.scatter(X[:,0],X[:,1],s=80,facecolors='none', edgecolors='r')
data = sio.loadmat("ex8data1.mat") X = data['X'] Xval = data['Xval'] #获取验证集 yval = data['yval'].flatten() mu,sigma2 = estimate_gussian(X) px = gaussian_distribution(Xval,mu,sigma2) eps,f1 = select_threshold(yval,px) anomaly_points = detection(X,eps,mu,sigma2) plt.figure() visualize_countours(mu,sigma2) circle_anomaly_points(anomaly_points) plt.scatter(X[:,0],X[:,1],c='b',marker='x',s=15,linewidths=1) plt.show()
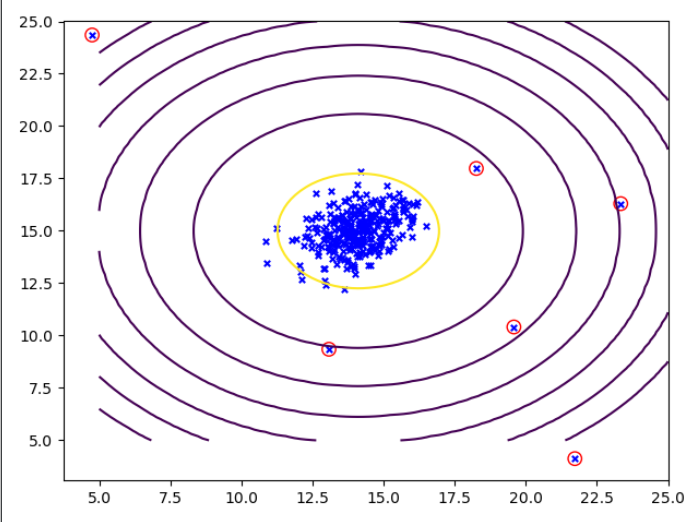
九：高维数据异常检测
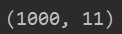
import numpy as np import matplotlib.pyplot as plt import scipy.io as sio def estimate_gussian(X): mu = np.mean(X,0) sigma2 = np.sum(np.power(X-mu,2),0)/X.shape[0] return mu,sigma2 def gaussian_distribution(X,mu,sigma2): #获取高斯模型p(x)值 p = (1/np.sqrt(2*np.pi*sigma2))*np.exp(-np.power((X-mu),2)/(2*sigma2)) return np.prod(p,axis=1) #横向累乘 def select_threshold(yval,pval): #yval是验证集标签 0或者1，pval是我们进行高斯处理后得到的概率在[0,1]之间 best_eps = 0 best_f1 = 0 for epsilon in np.linspace(np.min(pval),np.max(pval),num=1001): predictions = np.where(pval < epsilon, 1, 0) # 小于epsilon则预测为异常(为真） 满足条件返回1，不满足返回0 tp = np.sum(yval[np.where(predictions==1)]) #正确肯定 上面预测的为1，并且yval中也是1，我们才进行添加 fp = np.sum(np.where(yval[np.where(predictions==1)]==0,1,0)) #错误肯定 预测为真，实际为假 fn = np.sum(np.where(yval[np.where(predictions==0)]==1,1,0)) #错误否定 #计算查准率和查全率 if tp+fp == 0 or tp + fn ==0: continue prec = tp / (tp + fp) # 查准率 rec = tp / (tp + fn) # 查全率 #计算F1-score f1 = 2*prec*rec/(prec+rec) if f1 > best_f1: best_f1 = f1 best_eps = epsilon return best_eps,best_f1 def detection(X,eps,mu,sigma2): px = gaussian_distribution(X,mu,sigma2) #获取训练集的高斯分布值 #进行判断异常点 anomaly_points = X[np.where(px<eps)] return anomaly_points def visualize_countours(mu,sigma2): #绘制高斯分布等高线 #由上图可以知道，我们选取5-25，范围比较合适 x = np.linspace(5,25,100) y = np.linspace(5,25,100) xx,yy =np.meshgrid(x,y) X = np.c_[xx.flatten(),yy.flatten()] #数据对应网格中每一个点 z = gaussian_distribution(X,mu,sigma2).reshape(xx.shape) #获取每一个点坐标的高斯值 cont_levels = [10 ** h for h in range(-20, 0, 3)] #当z为当前列表的值才绘出等高线（最高1） 不设置的话，会比较奇怪 plt.contour(xx,yy,z,cont_levels) def circle_anomaly_points(X): #将异常点圈出 plt.scatter(X[:,0],X[:,1],s=80,facecolors='none', edgecolors='r') data = sio.loadmat("ex8data2.mat") X = data['X'] print(X.shape) Xval = data['Xval'] #获取验证集 yval = data['yval'].flatten() mu,sigma2 = estimate_gussian(X) px = gaussian_distribution(Xval,mu,sigma2) print(px) #(1000, 11) eps,f1 = select_threshold(yval,px) print(eps,f1) anomaly_points = detection(X,eps,mu,sigma2) print(anomaly_points)
