机器学习基础---无监督学习之K-Means算法
一:无监督学习
这里将介绍无监督学习中的聚类算法,这将是一个激动人心的时刻,因为这是我们学习的第一个非监督学习算法。我们将要让计算机学习无标签数据,而不是此前的标签数据.那么什么是无监督学习呢?
(一)有监督学习
首先,拿监督学习来进行比较,这是一个典型的监督学习的例子,有一个带标签的训练集,目标是找到一条能够区分正样本和负样本的决策边界,如下图:
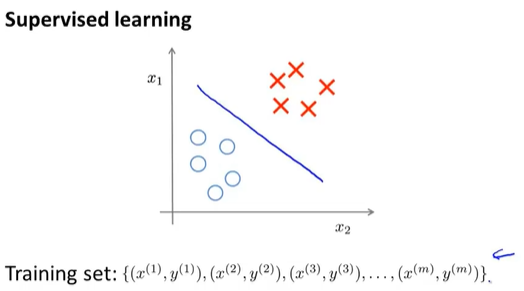
在一个典型的监督学习中,我们有一个有标签的训练集,我们的目标是找到能够区分正样本和负样本的决策边界,在这里的监督学习中,我们有一系列标签,我们需要据此拟合一个假设函数。
(二)无监督学习
与监督学习不同的是,在非监督学习中,我们的数据没有附带任何标签,我们拿到的数据就是这样的:
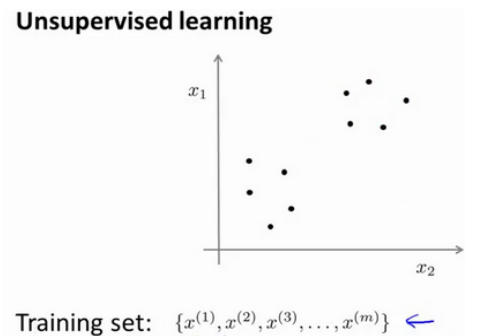
在这里我们有一系列点,却没有标签。
因此,我们的训练集可以写成只有x^(1),x^(2)…..一直到x^(m)。我们没有任何标签y。
因此,图上画的这些点没有标签信息。也就是说,在非监督学习中,我们需要将一系列无标签的训练数据,输入到一个算法中,然后我们告诉这个算法,快去为我们找找这个数据的内在结构给定数据。

我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集(称为簇),一个能够找到我圈出的这些点集的算法,就被称为聚类算法。
这将是第一个非监督学习算法。当然,此后还将提到其他类型的非监督学习算法,它们可以为我们找到其他类型的结构或者其他的一些模式,而不只是簇。
我们将先介绍聚类算法。此后,我们将陆续介绍其他算法。那么聚类算法一般用来做什么呢?

1.市场分割。也许你在数据库中存储了许多客户的信息,而你希望将他们分成不同的客户群,这样你可以对不同类型的客户分别销售产品或者分别提供更适合的服务。
2.社交网络分析:事实上有许多研究人员正在研究这样一些内容,他们关注一群人,关注社交网络,例如Facebook,Google+,或者是其他的一些信息,比如说:你经常跟哪些人联系,而这些人又经常给哪些人发邮件,由此找到关系密切的人群。因此,这可能需要另一个聚类算法,你希望用它发现社交网络中关系密切的朋友。
3.使用聚类算法来更好的组织计算机集群,或者更好的管理数据中心。因为如果你知道数据中心中,那些计算机经常协作工作。那么,你可以重新分配资源,重新布局网络。由此优化数据中心,优化数据通信。
4.研究如何利用聚类算法了解星系的形成。然后用这个知识,了解一些天文学上的细节问题。
二:K-均值算法(K-Means)
在聚类问题中,会给定一组未加标签的数据集,希望有一个算法能够自动地将这些数据分成有紧密关系的子集或簇。K-Means算法现在是最火热也是最为广泛应用的聚类算法,这里将介绍K-Means算法的定义及原理。
(一)K-均值算法原理
假设有一个无标签数据集如下图所示:
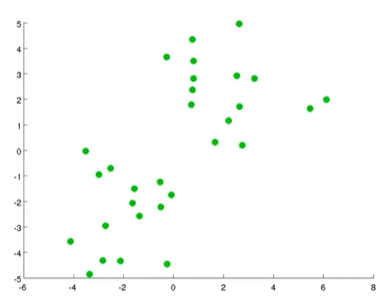
现在想将其分为两个簇,使用K-Means算法来进行操作,操作步骤:
1.首先随机生成两个点,这两点叫做聚类中心。
K-Means算法是一个迭代算法,它会做两件事,第一个是簇分配,第二个是移动聚类中心。
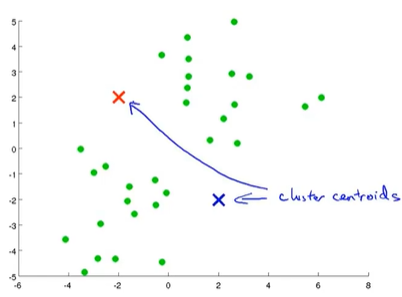
2.簇分配:K-Means算法中每次内循环的第一步要进行簇分配,也就是说,遍历每个样本点,根据每个样本与红色聚类中心更近还是蓝色中心更近来将每个样本点分配个两个聚类中心之一。具体的说,就是讲靠近蓝色聚类中心的点染成蓝色,靠近红色聚类中心的点染成红色。
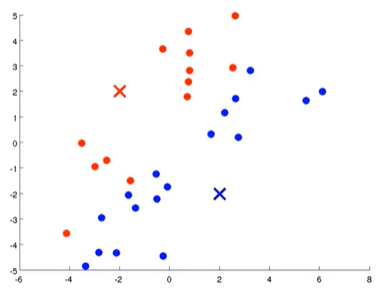
3.移动聚类中心:K-Means算法中每次内循环的第二步要移动聚类中心,要做是找到所有蓝点并计算出它们的均值,然后把蓝色聚类中心移到那里,红色聚类中心也是一样的操作。
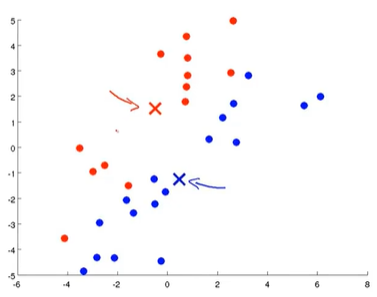
4.然后接着继续做簇分配和移动聚类中心,迭代多次之后,就会完成最终的两个点集的聚类,这就可以说K-Means算法已经聚合了。

(二)K-均值算法实现思路
1.算法输入
K是聚簇中心个数,第二个输入时训练集.
其中我们对应样本X^(i)时一个n维向量,默认丢弃x_0=1
2.算法伪代码

第一步:随机初始化K个聚类中心,μ_1,...,μ_K.
第二步:簇分配,遍历m个样本,判断每个样本到底距离哪一个聚簇中心更近,将其染成对应颜色(编号)
第三步:更新各个聚簇中心坐标,等于这个簇中所有点的均值
补充:对于一个没有点的聚簇中心,我们可以直接移除(例如我们设置K=3,而实际只有2个簇,则最后会移除掉一个)
(三) K-均值算法,解决分离不佳的簇
目前为止,K-Means算法都基于像下图中这样的数据集,它们很明显是可以分成3个簇的数据。
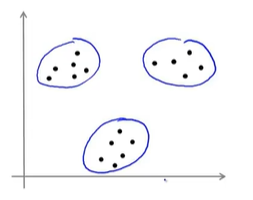
但在实际中,K-Means算法也会用于下图中这样的数据集,看起并不能很好地分成几个簇。
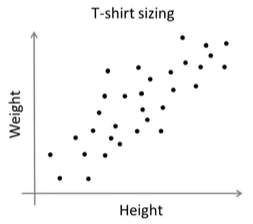
实际例子中,要根据顾客的身高体重来设计T-恤的尺寸,小号、中号、大号,那么3中尺码又该设计多大?有一个方法就是对上图中的数据集执行K-Means算法,算法可能会将数据分成下图中的3个簇。
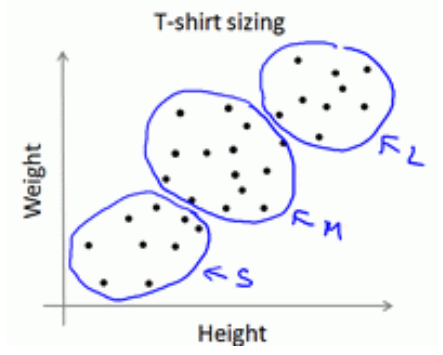
所以尽管数据集不是很明显的能分成3个簇,K-Means算法还是能将这些数据分为3个簇,这类似于市场细分的案例。
三:优化目标
类似于之前提到的线性回归、逻辑回归等算法,K-Means算法也有一个优化目标函数或者用于最小化的代价函数,这里将探讨这个优化目标函数是什么?
这里的学习主要有两方面的原因:
1.了解什么是K均值的优化目标函数,这将能帮助我们调试学习算法,确保K均值算法是在正确运行中 2.我们该怎样运用这个来帮助K均值找到更好的簇,并且避免局部最优解。
(一)3组变量进行跟踪
执行K-Means算法时,将会对3组变量进行跟踪。

1.

2. 

3.
(二)优化目标

这个代价函数有时也叫失真代价函数或者K-Means算法的失真。

在K-Means算法中:
第一步簇分配的步骤中,其实就是在最小化代价函数J。(分配点,不动聚簇中心)
第二步移动聚类中心的步骤中,其实就是选择μ值来最小化代价函数J。(只移动聚簇中心)
四:随机初始化
将讨论如何初始化K-Means算法,更重要的是探讨如何使算法避开局部最优。
(一)随机初始化聚簇中心

那么如何初始化聚类中心,这里有几种不同的方法可以用来随机初始化聚类中心。通常用下面的这种方法:
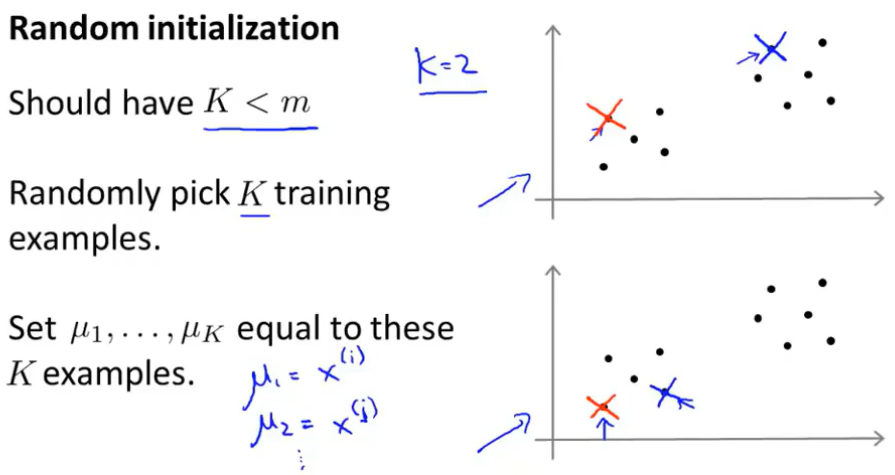
当运行K-Means算法时:
(1)应该把聚类中心的数值K设置为比训练样本数量m小的值;
(2)随机挑选K个训练样本;
(3)设定μ1,...,μk,让它们等于这K个样本。
这就是一个随机初始化聚类中心的方法,通过上面的两幅图,可能会猜到K-Means算法最终可能会收敛得到不同的结果,这取决于聚类的初始化状态---具体而言,K-均值算法可能会落在局部最优
比如:
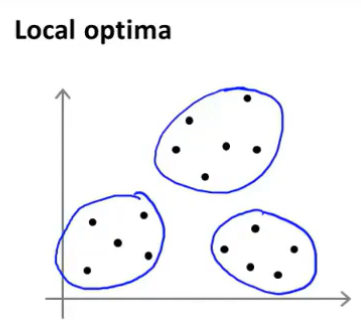
如果我们对上面训练集,随机初始化较好,那么我们就很容易获得3个不错的簇:
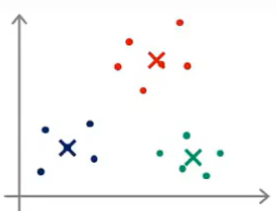
但是如果随机初始化得到的结果并不好,就可能会得到不同的局部最优值:
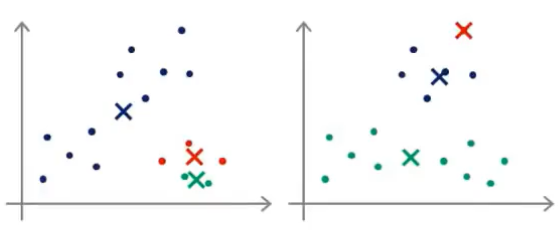
实际上,上述右图中的红色聚类只捕捉到了一个无标签的样本,而局部最优这个术语指的是代价函数J的局部最优。
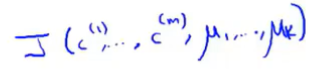
(二)避免局部最优
因此,如果想让找到最优可能的聚类,可以尝试多次随机初始化,以此来保证能够得到一个足够好的结果,下面是多次随机初始化的具体做法:

最后要做的是,在所有的100种分类数据的方法中选取代价最小的一个也就是代价函数J最小的。事实证明,在聚类数K较小的情况下(2~10个),使用多次随机初始化会有较大的影响,而如果K很大的情况,多次随机初始化可能并不会有太大效果。
五:选取聚类数量
将探讨K-Means算法如何去选择聚类数量或者说是如何选择参数K的值。
选择聚类数量并不容易,因为通常在数据集中有几个聚类是不清楚的,看下面这样的数据集,有时候会觉得有4个聚类,有时会觉得只有2个聚类。
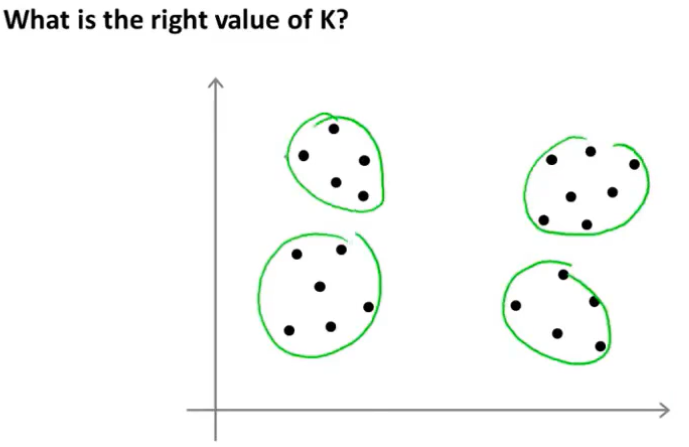
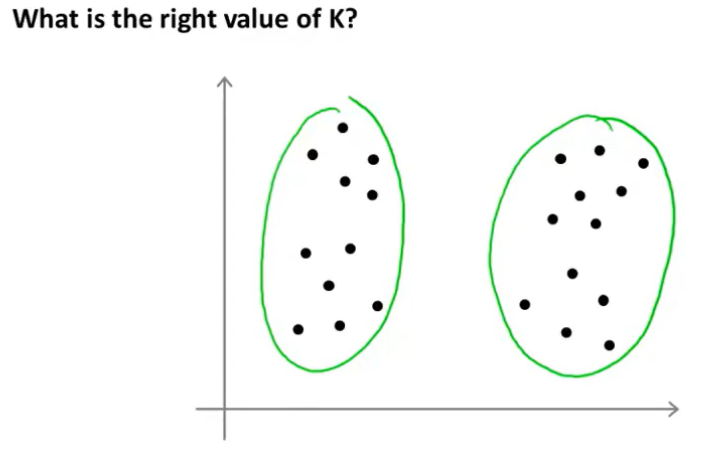
正是因为这样的原因,用一个自动化的算法来选择聚类数量是很困难的。
(一)肘部法则
当讨论选择聚类方法时,可能会谈到肘部法则这个方法,在肘部法则中,要做的是改变K也就是聚类总数。
先用一个类来聚类,这就意味着所有的数据都会分到一个类里,然后计算代价函数J。
用更多的类执行K-Means算法可能就会得到更小的J值,从下图中可以看到在K=3处有个突出来的部分,把这就叫作“肘部法则”。

当应用“肘部法则”时,遇到类似上图,这将是一种用来选择聚类个数的合理方法,但是“肘部法则”并不常用的原因是在实际运用到聚类问题上时,往往最后会得到一条看上去相当模糊的曲线,如下图:
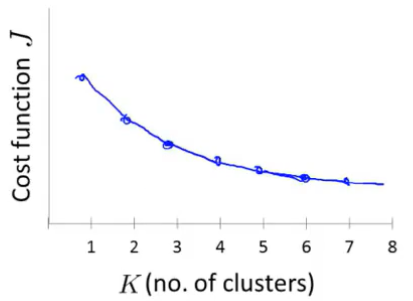
观察上图,看不到某个突出的点,看上去J值是连续下降的,所以这样并不能确定拐点合适的位置,这种情况下用“肘部法则”来选择聚类数目是很困难的。
(二)另外一种选择K值的思路:决定聚类数量更好的方式是看哪个聚类数量能更好地适应后续的目的(看需求)
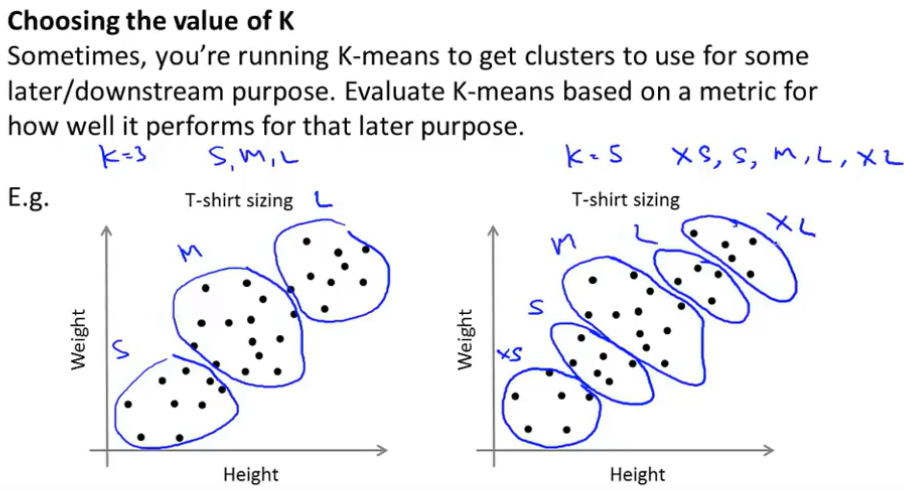
思考,如果有5个分类,T恤能否更好地满足顾客的需求?可以卖出多少T恤?客户是否会感到满意?所以考虑到后续的发展,就可以帮助你来选择是3种尺码好一些还是用5种尺码更适合。
(三)总结
大部分时候聚类数量K仍然是通过手动、人工输入或者经验来决定的,一种可以尝试方式是“肘部法则”,但不能期望它每次都有效果,选择聚类数量更好的思路是问自己运行K-Means算法的目的是什么,然后再决定聚类数量K取多少更好地服务于后续的目的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号