机器学习作业---支持向量机SVM（一）了解SVM
推文：支持向量机通俗导论（理解SVM的三层境界）
----------------线性核函数-----------------
一：作业介绍
在本练习的前半部分，您将使用支持向量机。各种示例2D数据集。使用这些数据集进行实验将帮助您直观地了解支持向量机如何工作，以及如何使用支持向量机的高斯内核。
二：导入数据和数据可视化
（一）数据导入
data = sio.loadmat("ex6data1.mat") X = data['X'] y = data['y'].flatten() m = y.size print(X.shape,y.shape)
（二）数据显示
print("X:\n",X[:10,]) print("y:\n",y[:10])
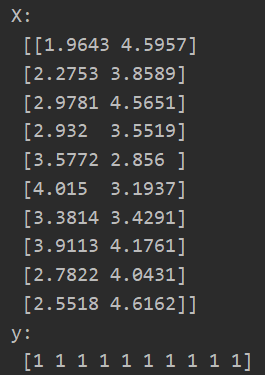
（三）数据可视化
def plot_data(X,y): posX = X[np.where(y==1)] #获取正样本 negX = X[np.where(y==0)] #获取负样本 plt.scatter(posX[:,0],posX[:,1],c='b',marker='X') #散点图绘制 正样本 plt.scatter(negX[:,0],negX[:,1],c='r',marker='o') #散点图绘制 负样本
plt.figure()
plot_data(X,y)
plt.show()
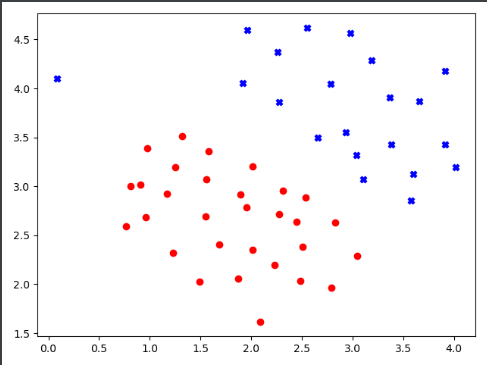
可以看出左上角的那个数据点为异常点（误差点）。
（四）获取横轴、、竖轴最值。后面绘制决策边界需要
print(np.min(X[:,0]),np.max(X[:,0])) #0.086405 4.015 print(np.min(X[:,1]),np.max(X[:,1])) #1.6177 4.6162
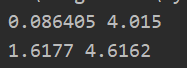
所以我们对于横轴取值范围为（-0.5，4.5），竖轴取值范围为（1.3，5）
三：svm模块之线性核函数
sklearn提供了很多机器学习的库，本次作业主要也是用它来解决SVM的问题
重点补充numpy.meshgrid()理解
https://blog.csdn.net/lllxxq141592654/article/details/81532855
（一）C=1时（C较小时，相当于入较大（平滑，泛化能力好），可能会导致欠拟合，高偏差），不因为一个异常点影响“大边界”
1.获取分类器的准确率
c = 1 clf = svm.SVC(c,kernel="linear",tol=1e-3) #实例化分类器，C为误差项惩罚系数，核函数选择线性核,停止训练的误差值大小，默认为1e-3。https://blog.csdn.net/weixin_41990278/article/details/93137009 clf.fit(X,y) #导入数据进行训练 print(clf.score(X,y)) #分类器的准确率
2.绘制决策边界《重点》
#绘制决策边界 def plot_boundary(model): x_min,x_max = -0.5,4.5 y_min, y_max = 1.3, 5 # 生成网格点坐标矩阵 xx,yy = np.meshgrid(np.linspace(x_min,x_max,500), #xx (500, 500) yy (500, 500) np.linspace(y_min,y_max,500)) # print(xx.shape,yy.shape) # print(np.c_[xx.flatten(), yy.flatten()].shape) #(250000, 2)--->对应了网格点坐标矩阵中的每一个坐标点 # 用训练好的分类器去预测各个坐标点中的数据的标签为[1]的值（其他为0）---全为1的位置就是决策边界 z = model.predict(np.c_[xx.flatten(), yy.flatten()]) #z (250000,) # print(z.shape) # for i in range(z.size): #z中全为0、1值 # if z[i] != 0: # print(z[i]) zz = z.reshape(xx.shape) #将我们预测出来的z值有一维空间，转换为二维网格坐标矩阵，便于在二维平面绘制决策边界 plt.contour(xx, yy, zz) #绘制决策边界 xx,yy是矩阵坐标，zz是我们对各个坐标的赋值，其中为1 的地方就是我们要找的决策边界
data = sio.loadmat("ex6data1.mat") X = data['X'] y = data['y'].flatten() m = y.size c = 1 clf = svm.SVC(c,kernel="linear",tol=1e-3) #实例化分类器，C为误差项惩罚系数，核函数选择线性核,停止训练的误差值大小，默认为1e-3。https://blog.csdn.net/weixin_41990278/article/details/93137009 clf.fit(X,y) #导入数据进行训练 plt.figure() plot_boundary(clf) plot_data(X,y) plt.show()
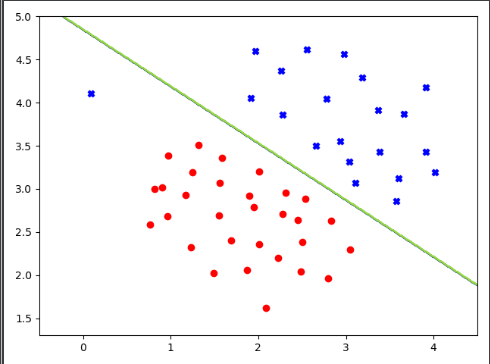
c＝1，此时不因为一个异常点影响“大边界”，拟合效果较好
（二）c＝100，可以很好的拟合正类和负类，但由于一个异常点造成过拟合，不能最大边界
----------------高斯核函数-----------------
一：数据导入及可视化
（一）数据可视化
data = sio.loadmat("ex6data2.mat") X = data['X'] y = data['y'].flatten() m = y.size plt.figure() plot_data(X,y) plt.show()
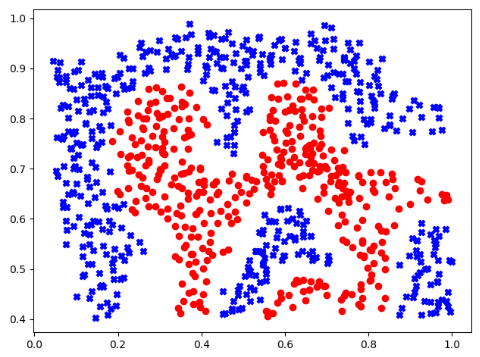
（二）获取数据上下界
print(np.min(X[:,0]),np.max(X[:,0])) #0.0449309 0.998848 print(np.min(X[:,1]),np.max(X[:,1])) #0.402632 0.988596
所以我们绘制决策边界时，取横坐标从（0，1）。竖轴（0.4，1）
二：svm模块之高斯核函数
使用高斯核函数解决线性不可分问题，并观察 σ取值对模型复杂度的影响。
（一）简单实现高斯核函数---测试
高斯核函数公式：
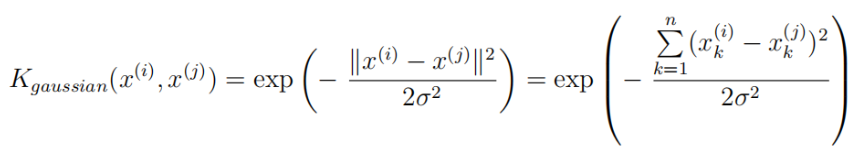
def gaussian_kernel(x1,x2,sigma=0.1): x1 = x1.flatten() x2 = x2.flatten() gk = np.exp(-np.sum(np.power((x1-x2),2))/(2*np.power(sigma,2))) return gk
x1 = np.array([1,2,1]) x2 = np.array([0,4,-1]) sigma = 2 print(gaussian_kernel(x1,x2,sigma))
（二）调用sklearn中的高斯核函数实现SVM算法
c = 1gamma = 1 clf = svm.SVC(c,kernel="rbf",gamma) #实例化分类器，C为误差项惩罚系数，核函数选择高斯核，设置gamma字段为gamma，注意gamma不等于σ，但是两者有关联。https://blog.csdn.net/weixin_41990278/article/details/93137009 clf.fit(X,y) #导入数据进行训练 print(clf.score(X,y)) #分类器的准确率
补充：SVM算法中的gamma字段《重点》
此外大家注意RBF公式里面的sigma和gamma的关系如下：
（三）绘制决策边界---修改坐标范围即可
#绘制决策边界 def plot_boundary(model): x_min,x_max = 0,1 y_min, y_max = 0.4, 1 # 生成网格点坐标矩阵 xx,yy = np.meshgrid(np.linspace(x_min,x_max,500), #xx (500, 500) yy (500, 500) np.linspace(y_min,y_max,500)) # print(xx.shape,yy.shape) # print(np.c_[xx.flatten(), yy.flatten()].shape) #(250000, 2)--->对应了网格点坐标矩阵中的每一个坐标点 # 用训练好的分类器去预测各个坐标点中的数据的标签为[1]的值（其他为0）---全为1的位置就是决策边界 z = model.predict(np.c_[xx.flatten(), yy.flatten()]) #z (250000,) # print(z.shape) # for i in range(z.size): #z中全为0、1值 # if z[i] != 0: # print(z[i]) zz = z.reshape(xx.shape) #将我们预测出来的z值有一维空间，转换为二维网格坐标矩阵，便于在二维平面绘制决策边界 plt.contour(xx, yy, zz) #绘制决策边界 xx,yy是矩阵坐标，zz是我们对各个坐标的赋值，其中为1 的地方就是我们要找的决策边界
plt.figure()
plot_boundary(clf)
plot_data(X,y)
plt.show()
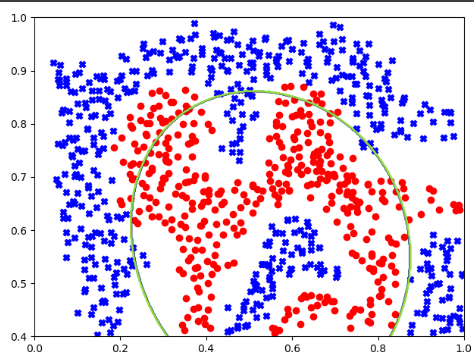
可以看出当gamma=1时，拟合效果并不是很好！！！
（四）不同gamma的选取
1.gamma=1时
分类器的准确率如下：
2.gamma=50
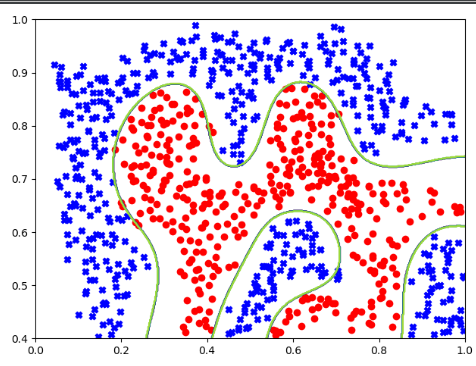
分类器的准确率如下：
3.gamma=1000
分类器的准确率如下：
（五）结论：σ和gamma
sigma和gamma的关系如下：
这里面大家需要注意的就是gamma的物理意义，就是大家提到很多的RBF的幅宽，它会影响每个支持向量对应的高斯的作用范围，从而影响泛化性能。
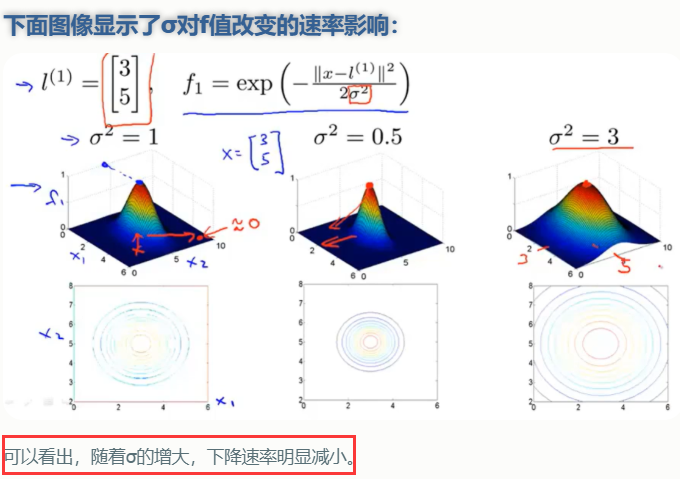
1.如果gamma设的太大，σ会很小，σ很小的高斯分布长得又高又瘦， 会造成只会作用于支持向量样本附近，对于未知样本分类效果很差，存在训练准确率可以很高，(如果让σ无穷小，则理论上，高斯核的SVM可以拟合任何非线性数据，但容易过拟合)而测试准确率不高的可能，就是通常说的过训练；
2.而如果gamma设的过小，σ会很大，则会造成平滑效应太大，无法在训练集上得到特别高的准确率，也会影响测试集的准确率。
----------------寻找最优参数 C 和 σ-----------------
一：SVM模型有两个非常重要的参数C与σ
（一）其中 C是惩罚系数，即对误差的宽容度。
1.c越高，入越小，容易过拟合。说明越不能容忍出现误差,
2.C越小，入越大，容易欠拟合。说明可以容忍出现误差,
C过大或过小，泛化能力变差
（二）σ隐含地决定了数据映射到新的特征空间后的分布
gamma是选择RBF函数作为kernel后，该函数自带的一个参数。
从gamma和σ之间关系，可以看出。gamma也隐含地决定了数据映射到新的特征空间后的分布
1.如果gamma设的太大，σ会很小，σ很小的高斯分布长得又高又瘦， 会造成只会作用于支持向量样本附近，对于未知样本分类效果很差，存在训练准确率可以很高，(如果让σ无穷小，则理论上，高斯核的SVM可以拟合任何非线性数据，但容易过拟合)而测试准确率不高的可能，就是通常说的过训练；
2.而如果gamma设的过小，σ会很大，则会造成平滑效应太大，无法在训练集上得到特别高的准确率，也会影响测试集的准确率。
二：加载数据及数据可视化
（一）绘制数据（训练集数据）
def plot_data(X,y): posX = X[np.where(y==1)] #获取正样本 negX = X[np.where(y==0)] #获取负样本 plt.scatter(posX[:,0],posX[:,1],c='b',marker='X') #散点图绘制 正样本 plt.scatter(negX[:,0],negX[:,1],c='r',marker='o') #散点图绘制 负样本
data = sio.loadmat("ex6data3.mat") X = data['X'] y = data['y'].flatten()
X = data['X']
y = data['y'].flatten()
Xval = data['Xval']
yval = data['yval'].flatten()
m = y.size
plt.figure()
plot_data(X,y)
plt.show()
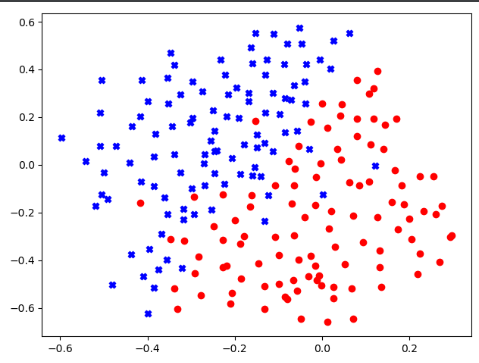
（二）获取数据最值
print(np.min(X[:,0]),np.max(X[:,0])) #-0.596774 0.297235 print(np.min(X[:,1]),np.max(X[:,1])) #-0.657895 0.573392
这里我们取横轴（-0.6，0.4），竖轴（-0.7，0.6）
三：根据验证集评分获取最优准确率和参数（C、σ)
def get_best_params(X,y,Xval,yval): # C 和 σ 的候选值 Cvalues = [3, 10, 30, 100, 0.01, 0.03, 0.1, 0.3, 1] # 9 gammas = [1, 3, 10, 30, 100, 0.01, 0.03, 0.1, 0.3] # 9 best_score = 0 #用于存放最佳准确率 best_params = (0,0) #用于存放参数C和σ for c in Cvalues: for gamma in gammas: clf = svm.SVC(c,kernel='rbf',gamma=gamma) clf.fit(X,y) # 用训练集数据拟合模型 score = clf.score(Xval,yval) # 用验证集数据进行评分 if score > best_score: best_score = score best_params = (c,gamma) return best_score,best_params
score, params = get_best_params(X,y,Xval,yval) print("score:\n",score) print("C gamma:\n",params)
注意：获取到的最优参数组合不只有一组（可能有多组的评分一样，都是最优，这里我们使用了>,所以只取了第一个最优的），更改候选值的顺序，最佳参数组合及其对应的决策边界也会改变。
四：根据我们获得的最优参数，绘制决策边界
#绘制决策边界 def plot_boundary(model): x_min,x_max = -0.6,0.4 y_min, y_max = -0.7,0.6 # 生成网格点坐标矩阵 xx,yy = np.meshgrid(np.linspace(x_min,x_max,500), #xx (500, 500) yy (500, 500) np.linspace(y_min,y_max,500)) # print(xx.shape,yy.shape) # print(np.c_[xx.flatten(), yy.flatten()].shape) #(250000, 2)--->对应了网格点坐标矩阵中的每一个坐标点 # 用训练好的分类器去预测各个坐标点中的数据的标签为[1]的值（其他为0）---全为1的位置就是决策边界 z = model.predict(np.c_[xx.flatten(), yy.flatten()]) #z (250000,) # print(z.shape) # for i in range(z.size): #z中全为0、1值 # if z[i] != 0: # print(z[i]) zz = z.reshape(xx.shape) #将我们预测出来的z值有一维空间，转换为二维网格坐标矩阵，便于在二维平面绘制决策边界 plt.contour(xx, yy, zz) #绘制决策边界 xx,yy是矩阵坐标，zz是我们对各个坐标的赋值，其中为1 的地方就是我们要找的决策边界
data = sio.loadmat("ex6data3.mat") X = data['X'] y = data['y'].flatten() Xval = data['Xval'] yval = data['yval'].flatten() score, params = get_best_params(X,y,Xval,yval) c = params[0] gamma = params[1] clf = svm.SVC(c,kernel="rbf",gamma=gamma) #实例化分类器，C为误差项惩罚系数，核函数选择线性核,停止训练的误差值大小，默认为1e-3。https://blog.csdn.net/weixin_41990278/article/details/93137009 clf.fit(X,y) #导入数据进行训练 plt.figure() plot_boundary(clf) plot_data(X,y) plt.show()
