机器学习作业---偏差和方差(线性回归)错误反例,但是理清了代码思路,很重要
重点思考排错:关于高级优化算法scipy.optimize.minimize
(一)代价函数和梯度求解
在代价函数和梯度求解中,我们要多次用到矩阵乘法。
1.numpy.matrix(不推荐)
所以一开始,我使用了numpy.matrix()方法,将我传入的θ、X、y等向量(是numpy.ndarray数组类型),全部转换为matrix类型,进行矩阵运算
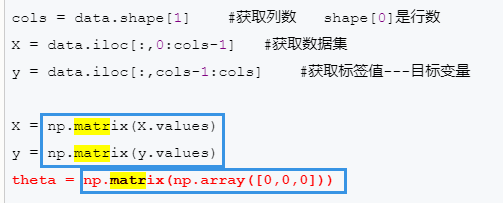
但是在使用过程中,发现编译器并不推荐使用该方法,因为:
1.我们需要将传入的参数进行转换,降低了效率
2.如果一个程序里面既有matrix 又有array,会让人脑袋大。但是如果只用array,你不仅可以实现matrix所有的功能,还减少了编程和阅读的麻烦。
2.numpy.ndarray+@---解决部分问题,但是使用的方法有点问题
在使用过程中,我发现对于numpy.ndarray类型数据,如果要进行矩阵运算,那么数组必须是二维数组[[]]
这里我经常用@将ndarray进行矩阵运算
但是在使用过程中,发现一个错误用法。就是我们如果对于一个ndarray类型数据,是一维数组,那么似乎矩阵运算并不能按照我们的想法进行:
1.比如进行转置T操作:
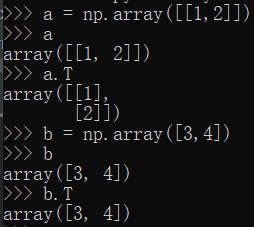
2.比如进行矩阵乘法操作:

可以看到,虽然结果是一样的,但是返回的分别是二维和一维数组。而且我们对一维数组的转置,存在部分疑问?因为转置后还是行向量显示,结果却是按照列向量计算
3.numpy.ndarray+dot点乘处理,避免2中问题
当我们传入两个一维数组时:

是进行点乘处理的。
当我们传入一个二维和一维数组时:---两个向量必须同维度(得到的结果是矩阵乘积)


总结:推荐使用第三种用法---其中另一个原因看下面
(二)高级优化算法scipy.optimize.minimize解析
调用:
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
参数:
fun :优化的目标函数
x0 :初值,一维数组,shape (n,)
args : 元组,可选,额外传递给优化函数的参数
method:求解的算法,选择TNC则和fmin_tnc()类似
jac:返回梯度向量的函数
返回:
返回优化结果对象,x:优化问题的目标数组。success: True表示成功与否,不成功会给出失败信息。
注意重点:
1.我们返回的参数θ向量就是返回的优化结果对象x。
2.我们返回的优化结果对象x是一个numpy.ndarray类型的一维数组,所以我们可以认为,在我们中间进行计算过程中:
我们使用梯度求解函数求解出来的θ参数向量也应该是一个一维数组,同时在优化函数中会将梯度求解结果作为参数传入到代价函数中,求解代价误差。所以在中间黑盒过程中,默认传递的就是一维数组(上面参数中说明了,因为我们传入的θ向量默认是放入x0中)。所以对于我们写的求解代价函数,传入的θ参数也应该是一维数组。
3.我们只提供了一个x0和args参数,所以我们要保证我们的fun传入的代价函数和jac传入的梯度求解函数的参数保持一致
4.我们可以使用一个函数,返回梯度和代价误差,只需要设置jac=True即可
minimize(fun=backporp,x0=theta_param,args=(input_size,hidden_size,num_labels,X,y_onehot,1),method='TNC',jac=True,options={'maxiter':250})
(三)补充fmin_tnc()
有约束的多元函数问题,提供梯度信息,使用截断牛顿法。
调用:
scipy.optimize.fmin_tnc(func, x0, fprime=None, args=(), approx_grad=0, bounds=None, epsilon=1e-08, scale=None, offset=None, messages=15, maxCGit=-1, maxfun=None, eta=-1, stepmx=0, accuracy=0, fmin=0, ftol=-1, xtol=-1, pgtol=-1, rescale=-1, disp=None, callback=None)
最常使用的参数:
func:优化的目标函数
x0:初值
fprime:提供优化函数func的梯度函数,不然优化函数func必须返回函数值和梯度,或者设置approx_grad=True
approx_grad :如果设置为True,会给出近似梯度
args:元组,是传递给优化函数的参数
返回:
x : 数组,返回的优化问题目标值
nfeval : 整数,function evaluations的数目
在进行优化的时候,每当目标优化函数被调用一次,就算一个function evaluation。在一次迭代过程中会有多次function evaluation。这个参数不等同于迭代次数,而往往大于迭代次数。
rc : int,Return code, see below
一:方差、偏差问题回顾
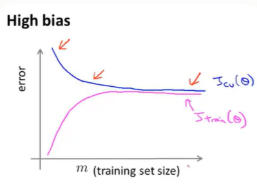
(一)高偏差(欠拟合)
1.当m较小时:比如m=1,这是完全拟合,所以训练误差从0开始。当逐渐增大样本数量,训练误差逐渐增大。同样,当m较小时,验证误差最大,当m逐渐增大,则验证误差减小。
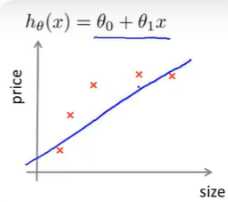
2.当我们增大样本容量时:对于这组数据这是拟合得最好得直线,当我们增大样本容量后,直线拟合得越来越好---即J_cv逐渐减小
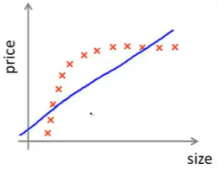
总结:
训练误差一开始也是很小的,而在高偏差的情况下,你会发现训练集误差会逐渐增大,最后接近交叉验证误差
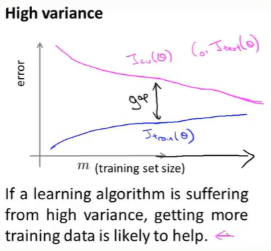
(二)高方差(过拟合)
1.训练误差---当训练样本越多的时候,就越难把训练集数据拟合得更好。但总的来说训练集误差还是很小得

2.交叉验证误差---过拟合下(泛化能力很差),验证误差将会一直很大,尽管随着样本增大,但是总的来说还是很大

其特点是:在训练误差和交叉验证误差之间有一段很大的差距。
当我们增大样本数量时,训练误差会增大,而验证误差会减少。所以高方差下,增大样本数量还是有用的。
(三)简单总结
训练集误差和交叉验证集误差近似时:偏差/欠拟合
交叉验证集误差远大于训练集误差时:方差/过拟合
二:正则化和方差、偏差

(一)当我们设置入较大时
比如入=1000,这时θ_1,...,θ_m都将受到很大的惩罚。所以θ_1,...,θ_m几乎都等于0.这时H_θ(x)≈θ_0
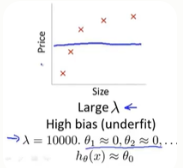
因此这个假设处于高偏差,对数据集严重欠拟合。
(二)设置入较小时
与之对应的另一种情况是,如果我们的lambda值很小,比如说lambda的值等于0的时候,在这种情况下,如果我们要拟合一个高阶多项式的话,那么此时我们通常会处于过拟合的情况。
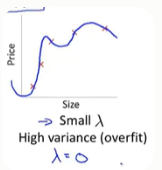
(三)合适大小入
只有当我们取一个中间大小的,既不大也不小的lambda值时,我们才会得到一组合理的,对数据刚好拟合的theta参数值
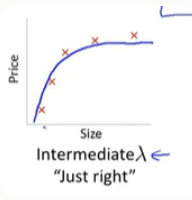
(四)总结
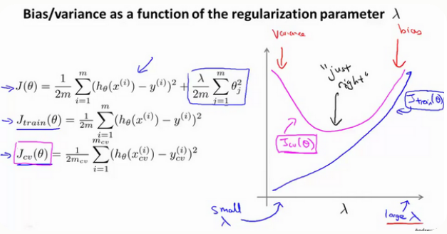
• 当入较小时,训练集误差较小(过拟合)而交叉验证集误差较大--高方差
• 随着入的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加---高偏差
注意:训练集误差是指内部数据集与模型的拟合程度(所以当入小的时候,模型虽然是过拟合,但是与原来训练集的拟合程度还是不错的),验证集误差是指新的数据集与原始模型的平均误差平方和(当入过小或者过大,都会导致误差太大)。
三:数据加载、显示----后面可能都有问题
(一)代码实现数据加载、显示
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as sio
import scipy.optimize as opt
data = sio.loadmat("ex5data1.mat")
X = data['X']
y = data['y']
Xval = data['Xval']
yval = data['yval']
Xtest = data['Xtest']
ytest = data['ytest']
plt.figure()
plt.scatter(X,y,c='r',marker='o')
plt.xlabel("Change in water level (x)")
plt.ylabel("Water flowing out of the dam (y)")
plt.show()

(二)数据展示
print("X.shape X")
print(X.shape)
print(X)
print("y.shape y")
print(y.shape)
print(y)
print("----------------------")
X.shape X
(12, 1)
[[-15.93675813]
[-29.15297922]
[ 36.18954863]
[ 37.49218733]
[-48.05882945]
[ -8.94145794]
[ 15.30779289]
[-34.70626581]
[ 1.38915437]
[-44.38375985]
[ 7.01350208]
[ 22.76274892]]
----------------------
y.shape y
(12, 1)
[[ 2.13431051]
[ 1.17325668]
[34.35910918]
[36.83795516]
[ 2.80896507]
[ 2.12107248]
[14.71026831]
[ 2.61418439]
[ 3.74017167]
[ 3.73169131]
[ 7.62765885]
[22.7524283 ]]
print("----------------------")
print("Xval.shape yval.shape")
print(Xval.shape,yval.shape)
print("----------------------")
print("Xtest.shape ytest.shape")
print(Xtest.shape,ytest.shape)

二:正则化线性回归代价函数
(一)代价函数
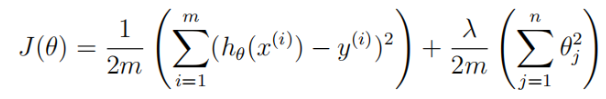
def reg_cost(theta,X,y,lamda=1):
m = X.shape[0]
return 1/(2*m)*np.sum(np.power(X@theta.T-y,2))+lamda/(2*m)*np.sum(np.power(theta,2))
cost = reg_cost(theta,X,y,0)
print(cost)

(二)正则化梯度求解----主要出错地点
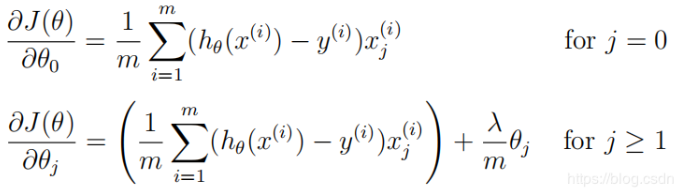
def reg_gradient(theta,X,y,lamda=1):
m = X.shape[0]
error = X@theta.T-y
theta_grad = error.T@X/m
theta_grad[0,1:] += theta[0,1:]*lamda/m
return theta_grad
grad = reg_gradient(theta,X,y,0)
print(grad)

grad = reg_gradient(theta,X,y,1)
print(grad)

三:高级优化算法求解参数
#导入数据
data = sio.loadmat("ex5data1.mat")
X = data['X']
y = data['y']
Xval = data['Xval']
yval = data['yval']
Xtest = data['Xtest']
ytest = data['ytest']
theta = np.array([np.ones(2)])
X = np.c_[np.ones(X.shape[0]),X]
res = opt.minimize(fun=reg_cost,x0=theta,args=(X,y,1),method="TNC",jac=reg_gradient,options={'disp':True})
theta_new = res.get('x')
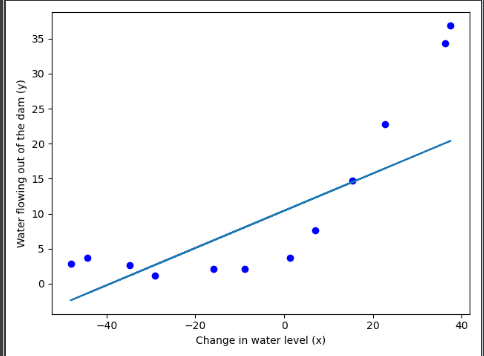
plt.figure()
plt.scatter(X[:,1],y,c='b',marker='o')
plt.plot(X[:,1],X[:,1]*theta_new[1]+theta_new[0])
plt.xlabel("Change in water level (x)")
plt.ylabel("Water flowing out of the dam (y)")
plt.show()

这里就已经出错了,最后求解的参数向量不对!!!
四:绘制学习曲线---开始明显出错(只要出现错误是在梯度求解函数中)

注意:
1.使用训练集的子集来拟合数据--获取本次循环最优参数
2.在计算训练代价(误差)和交叉验证代价(误差)时,不需要使用正则化
3.使用相同的验证集自己来计算训练代价
(一)获取训练误差和验证误差
def learning_curve(X,y,Xval,yval,lamda):
m = X.shape[0]
#训练集误差和验证集误差
error_train = np.zeros(m)
error_val = np.zeros(m)
#从一个训练样本开始逐个增加
for i in range(m):
X_temp = X[:i+1,:] #获取新的临时训练样本集---注意事项1
y_temp = y[:i+1,:]
#获取当前训练集样本下的最优参数θ向量
res = opt.minimize(fun=reg_cost,x0=theta,args=(X_temp,y_temp,lamda),method="TNC",jac=reg_gradient,options={'disp':False})
#根据上面获得的最优参数向量,我们获取训练集误差---注意:训练集误差的数据集来自于我们新的训练集
theta = np.array([res.x])
error_train[i] = reg_cost(theta,X_temp,y_temp,lamda)
#验证集误差,数据集来自于全部验证集
error_val[i] = reg_cost(theta,Xval,yval,lamda) #每次都是将所有验证集进行计算误差----注意事项3
return error_train,error_val
#绘制学习曲线
error_train,error_val = learning_curve(X,y,Xval,yval,0) #设置lamda为0,不进行正则化处理---注意事项2
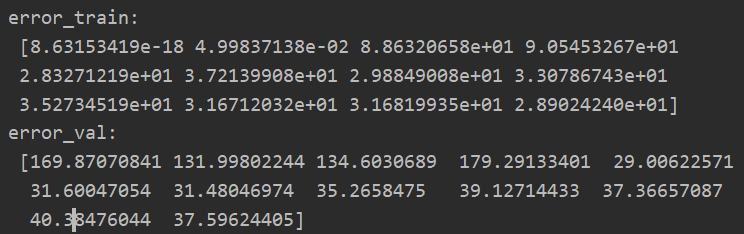
print("error_train:\n",error_train)
print("error_val:\n",error_val)
(二)绘制学习曲线
#绘制学习曲线 error_train,error_val = learning_curve(X,y,Xval,yval,0) plt.figure() plt.plot(np.arange(X.shape[0]),error_train,np.arange(X.shape[0]),error_val) plt.title("Learning Curve for linear regression") plt.xlabel("Number of Training Examples") plt.ylabel("Error") plt.legend(['Train','Cross Validation']) plt.show()
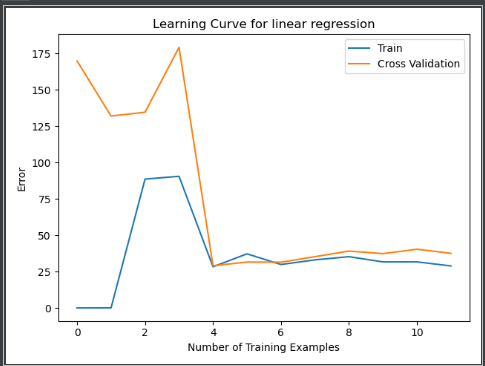
这里就发现了,和我们真正要展示的学习曲线有所差异:
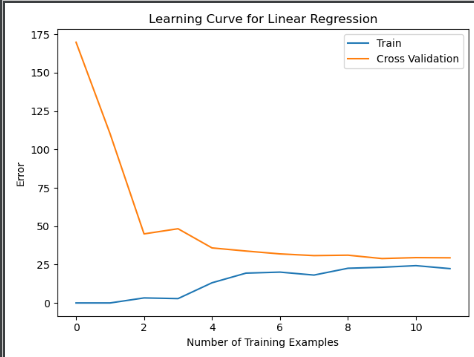
太过混乱,不进行修改!!!!
作者:山上有风景
欢迎任何形式的转载,但请务必注明出处。
限于本人水平,如果文章和代码有表述不当之处,还请不吝赐教。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
2018-05-14 Python环境安装