机器学习基础---神经网络（调试优化）（随机初始化、梯度检测）

一：随机初始化

当我们使用梯度下降法或者其他高级优化算法时，我们需要对参数θ选取一些初始值。对于高级优化算法，会默认认为我们已经为变量θ设置了初始值：

同样，对于梯度下降法，我们也需要对θ进行初始化。之后我们可以一步一步通过梯度下降来最小化代价函数J，那么如何来对θ进行初始化值呢？

（一）将θ全部设置为0---神经网络中不适用

尽管在逻辑回归中，可以这样使用。但是在实际神经网络训练中起不到作用。

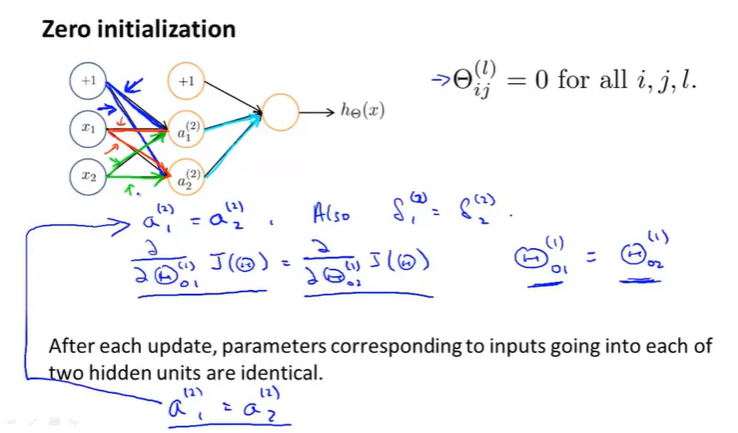
如果我们初始化所有θ全为0（全部相等）：

 

那么对于每个隐藏单元的输入基本都是一样的：

所以求得的偏导也是一致的，

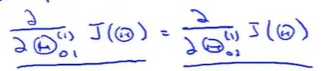
当我们只是设置了一个步长，那么对于每次参数的更新以后。各个隐藏单元的权重还是一致的。

这就意味着这个神经网络计算不出很好的函数，当我们有很多的隐藏单元时，所有的隐藏单元都在计算相同的特征，都在以相同的函数作为输入。---高度冗余。所以无论后面有几个输出单元，最终只能得到一个特征，这种情况阻止了神经网络学习有趣的东西

（二）随机初始化---解决上面所有权重都相等的问题（对称问题）

 

（三）代码实现

def rand_initiation(l_in,l_out):    #对于相邻两层
    w = np.zeros((l_out,l_in+1))  #需要加上前面一层的偏执单元权重
    eps_init = 0.12 #接近0，保持在-ε到ε之间
    w = np.random.rand(l_out,l_in+1)*2*eps_init-eps_init
    return w

w = rand_initiation(3,5)
print(w.shape)
print(w)

或者使用下面方法实现随机初始化：

def debug_initialize_weights(fan_in,fan_out):
    w = np.zeros((fan_out,1+fan_in))
    w = np.sin(np.arange(w.size)).reshape(w.shape) / 10　　#使用sin保证值在（-1，1）之间，再除以10，则值在（-0.1，0.1）之间初始化
    return w

w = debug_initialize_weights(3,5)
print(w.shape)
print(w)

二：梯度检验--确保我们实现的反向传播代码正确性

（一）反向传播存在的问题

前面我们学习了如何使用神经网络中的前向传播和反向传播算法计算导数，但是反向传播算法含有许多细节，而且实现比较复杂，并且由一个不好的特性：

当反向传播与梯度下降或是其他算法一同工作时，可能会存在一些不容易察觉的错误，意味着，虽然代价函数J看上去在不断减小，但最终的结果可能并不是最优解。其误差会比无Bug的情况下高出一个量级。并且我们很可能不知道我们所出现的问题是由Bug导致的。

解决方法：---梯度检验

几乎可以解决所有这种问题。几乎在所有反向传播，或者其他类似梯度下降算法使用的同时，都会进行梯度检验。他将保证前向传播已经后面的反向传播是完全正确的。

可以用于验证自己写的代码确实能够正确的计算出代价函数J的导数

（二）定义法求解导数

当θ是一个向量时，我们则需要对偏导数进行检验：

（三）算法实现

n代表了θ参数维度，我们对每一个θ_i执行上面的求导方法。之后检验我们使用导数定义求得的导数和使用反向传播求得的导数是否接近（几位小数差距）或者相等。那么我们就可以确定反向传播的实现是正确的。可以很好的优化J(θ)

注意：我们只需要使用一次梯度检验来检验我们反向传播算法求得的导数是否正确。如果正确，那么我们后面的学习就需要关闭梯度检验（因为使用梯度检验计算量大、且慢）

注意:简单的梯度检验 利用数值估计的梯度和真实的梯度二范数之差除以二范数值之和就是误差

（四）代码实现 

def compute_numerial_gradient(cost_func,theta): #用于计算梯度
    numgrad = np.zeros(theta.size)  #保存梯度
    perturb = np.zeros(theta.size)  #保持每一次计算梯度，只有一个维度的θ_j可以减去ε
    e = 1e-4

    for i in range(theta.size):
        perturb[i] = e
        J_1 = cost_func(theta-perturb)
        J_2 = cost_func(theta+perturb)

        numgrad[i] = (J_2-J_1)/(2*e)
        perturb[i] = 0  #需要将修改的位置数据还原

    return numgrad

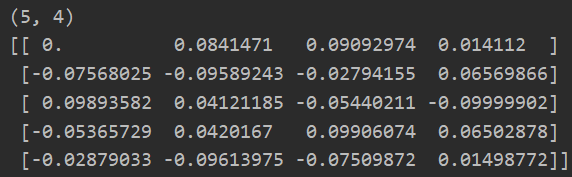
def check_gradients(lamda):
    #因为一个真的训练集数据太大，所以我们这里随机生成一些小规模数据，进行计检验
    input_layer_size = 3    #输入层
    hidden_layer_size = 5   #隐藏层
    num_labels = 3          #输出层---分类数

    m = 5   #数据集条数

    #初始化权重参数
    theta1 = debug_initialize_weights(input_layer_size,hidden_layer_size)
    theta2 = debug_initialize_weights(hidden_layer_size,num_labels)

    #同理：初始化一些训练集X和标签值y
    X = debug_initialize_weights(input_layer_size - 1,m)    #训练集是m行，input_layer_size列
    y = 1 + np.mod(np.arange(1,m+1),num_labels) #取余分类别1->num_labels
    encoder = OneHotEncoder(sparse=False)   #sparse=True 表示编码的格式，默认为 True，即为稀疏的格式，指定 False 则就不用 toarray() 了
    y_onehot = encoder.fit_transform(np.array([y]).T)   #需要y是列向量

    #展开参数
    theta_param = np.concatenate([np.ravel(theta1),np.ravel(theta2)])

    #1.使用导数定义求偏导
    def cost_func(theta_p):
        return cost(theta_p,input_layer_size,hidden_layer_size,num_labels,X,y_onehot,lamda)  #代价函数求偏导J(θ)

    numgrad = compute_numerial_gradient(cost_func,theta_param)
    #2.使用反向传播求偏导
    J,grad = backporp(theta_param,input_layer_size,hidden_layer_size,num_labels,X,y_onehot,lamda)
    print(np.c_[grad,numgrad,grad-numgrad])   #进行结果输出，对比

check_gradients(0)　　#修改lamda还是很接近的

可以看出我们使用导数定义求得的导数和使用反向传播求得的导数十分接近！！！

所以：我们的反向传播算法是正确的！！！