机器学习作业---神经网络实现多类分类

一：神经网络实现识别手写数字

使用神经网络再次实现处理手写数字数据集。通过反向传播算法实现神经网络成本函数和梯度计算得非正则化和正则化版本。还将实现随机权重初始化和使用网络进行预测得方法。

（一）导入库，并且读取数据集

因为我们的数据集类型是.mat文件（是在matlab的本机格式），所以在使用python加载时，我们需要使用一个SciPy工具。

import numpy as np
import pandas as pd
import matplotlib as plt
from scipy.io import loadmat    #用于载入matlab文件

data = loadmat('ex3data1.mat')  #加载数据
print(data)

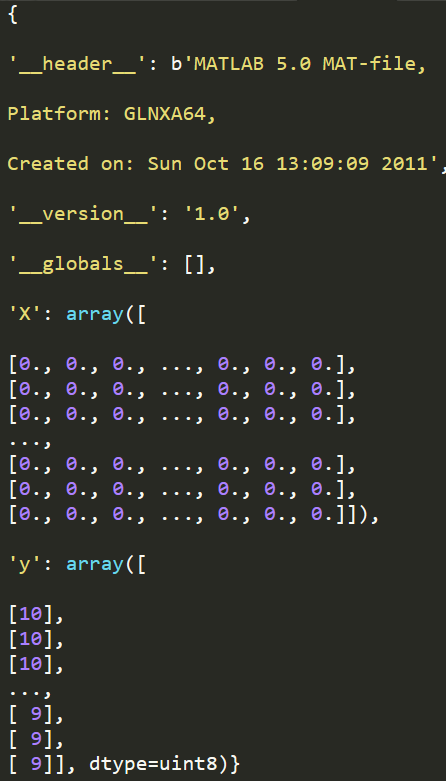
print(data['X'].shape)
print(data['y'].shape)

图像在martix X中表示为400维向量（其中有5000个数据）。400维“特征”是原始图像（20X20)图像中每个像素的灰度强度。

类标签在向量y中作为图像中数字的数字类。

第一个任务是将我们的逻辑函数实现修改为完全向量化（即没有for循环）。这是因为向量化代码除了简洁外，还能利用线性代数进行优化。

并且通常比迭代代码快得多。

（二）部分数据可视化（5000中，随机选取100个显示）

def displayData(X,example_width=None):  #显示20x20像素数据在一个格子里面
    if example_width is None:
        example_width = math.floor(math.sqrt(X.shape[1]))   #X.shape[1]=400
    print(X.shape)
    #计算行列
    m,n = X.shape   #返回的是我们随机选取的100行样本---（100，400）

    #获取图像高度
    example_height = math.ceil(n/example_width) #400/20 = 20

    # 计算需要展示的图片数量
    display_rows = math.floor(math.sqrt(m)) #10
    display_cols = math.ceil(m / display_rows)  #100/10=10

    fig,ax = plt.subplots(nrows=display_rows,ncols=display_cols,sharey=True,sharex=True,figsize=(12,12)) #https://blog.csdn.net/qq_39622065/article/details/82909421

    #拷贝图像到子区域进行展示
    for row in range(display_rows):
        for col in range(display_cols):
            ax[row,col].matshow(X[display_rows*row+col].reshape(example_width,example_height),cmap='gray') #希望将矩阵以图形方式显示https://www.cnblogs.com/shanger/articles/11872437.html

    plt.xticks([])  #用于设置每个小区域坐标轴刻度，设置为空，则不显示刻度
    plt.yticks([])

    plt.show()

plt.rcParams['figure.dpi'] = 200
data = loadmat('ex3data1.mat')  #加载数据
# print(data['X'].shape)
# print(data['y'].shape)
X = data.get('X')
y = data.get('y')
sample_idx = np.random.choice(np.arange(X.shape[0]),100)    #随机选取100个数（100个样本的序号）
# print(sample_idx)
samples = X[sample_idx,:]   #获取上面选取的索引对应的数据集
smaples_y = y[sample_idx,:] #可以知道我们选取的数字标签值
# print(smaples_y)
displayData(samples)  #进行展示

（三）对y标签值进行one-hot编码

举例（1）：one-hot编码

from sklearn.preprocessing import OneHotEncoder  
import numpy as np 

a = np.array([[1,2,3,4,5，5，3，0,6,7,8,9,0]]) 
b = a.T 

c = encoder.fit_transform(b) 

可以看出下列对应关系：

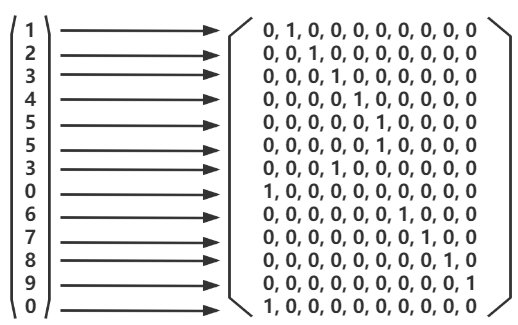
举例（2）：one-hot编码

总之：one-hot编码，会根据我们标签值中的分类数（实验中是10个），生成相应的维度。每个标签值对应唯一一个行向量（该向量中只有一个1，其他全为0）

（详细案例可以见--五：利用神经网络解决多类别分类问题）

将输出得多分类标签值y（这里共10类），进行编码，都转换为一个10维列向量。

from sklearn.preprocessing import OneHotEncoder #预处理操作

encoder = OneHotEncoder(sparse=False)   #sparse=True 表示编码的格式，默认为 True，即为稀疏的格式，指定 False 则就不用 toarray() 了
y_onehot = encoder.fit_transform(y)

print(y.shape)
print(y_onehot.shape)

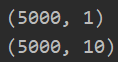
print(y[0])　　#简单查看编码内容
print(y_onehot[0,:])

（四）神经网络结构图

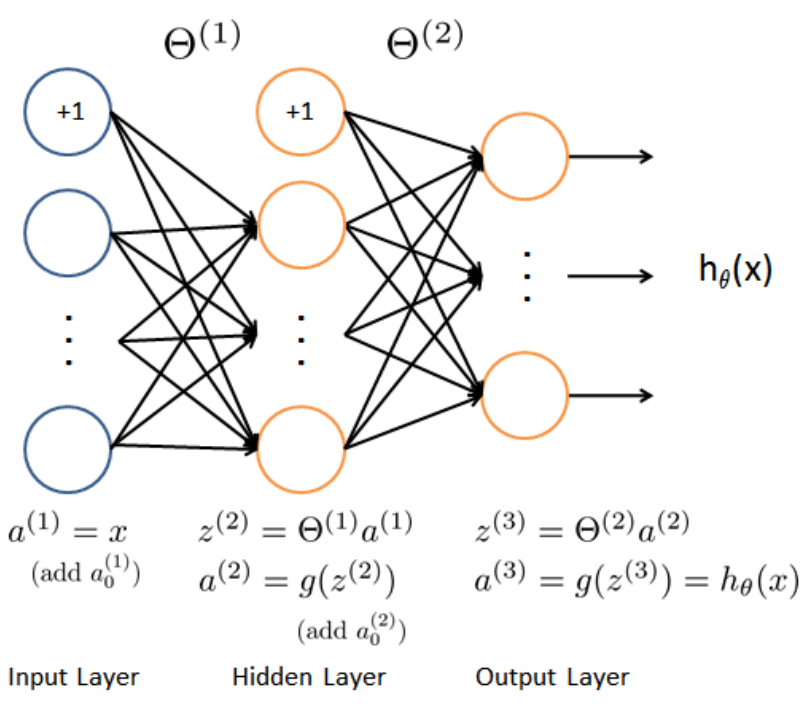
我们要为实验构建的神经网络：

输入层：包括400个特征（20X20），加一个偏置单元。

隐藏层：25个单位的隐藏层（详细见下面），加一个偏置单元

输出层：根据我们的分类，设置10个输出单元

这里，我们已经提供了一系列的神经网络参数：θ⁽¹⁾和θ⁽²⁾---即全部的权重参数（已经提前为我们训练过了，存储在ex4weights.mat）。这些参数是取决于我们的第二层隐藏层单元数（由于ex4weights.mat文件提供了全部参数，所以同时也要配置隐藏层单元数---25）---这里是从文件中获取θ的初始值，然后进行迭代下降（我们会在后面提到随机初始化方法，用来放置参数对称问题）

theta_data = loadmat('ex4weights.mat')  #加载数据
theta_1 = theta_data.get('Theta1')
theta_2 = theta_data.get('Theta2')
print(theta_1.shape)
print(theta_2.shape)

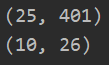
（五）实现sigmoid函数

def sigmoid(z): #实现sigmoid函数
    return 1/(1+np.exp(-z))

（六）实现前向传播函数---计算各个层（各个节点）的激活值

各层单元数变化如下：

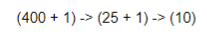
神经网络结构：

def forward_propagate(X, theta1, theta2):   #X是我们输入层训练集，theta1是我们第一层的参数，theta2是我们的第二层参数
    #首先，我们要为输入数据集X，添加偏置单元
    a1 = np.insert(X,0,1,axis=1)    #插入一列全为1的列向量到X中
    #计算第二层激活值
    z2 = a1@theta1.T    #theta1是一个(25，401)矩阵，a1是（5000，401）---z2是（5000，25）
    a2 = np.insert(sigmoid(z2),0,1,axis=1)   #.之后添加偏置单元。变为（5000，26）
    #计算第三层激活值
    z3 = a2@theta2.T    #theta2是一个（10，26）矩阵，a2是（5000，26），所以z3是一个（5000，10）矩阵
    h = sigmoid(z3) #获取假设函数值

    return a1,z2,a2,z3,h

theta_data = loadmat('ex4weights.mat')  #加载数据
theta_1 = theta_data.get('Theta1')
theta_2 = theta_data.get('Theta2')
a1,z2,a2,z3,h = forward_propagate(X,theta_1,theta_2)

（七）代价函数---最好保持同下面梯度函数参数一致

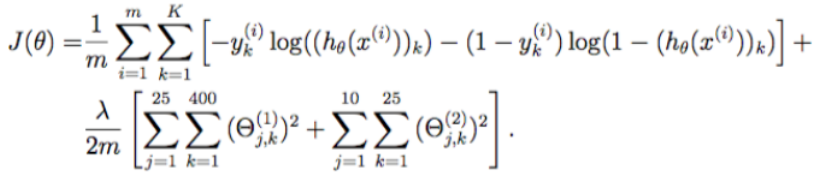
def cost(theta_param,input_size,hidden_size,num_labels,X,y,lamda=1):  #lamda是正则化参数
    #获取样本个数
    m = X.shape[0]

    theta_1 = theta_param[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
    theta_2 = theta_param[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

    #将获得神经元单元激活值等信息
    a1,z2,a2,z3,h = forward_propagate(X,theta_1,theta_2)
    #初始化代价函数
    J = 0

    #根据公式计算代价函数
    for i in range(m):  #遍历每一个样本---m
        first_term = np.multiply(-y[i,:],np.log(h[i,:]))    #标签向量，乘以假设函数矩阵---K
        second_term = np.multiply((1-y[i,:]),np.log(1-h[i,:]))
        J += np.sum(first_term-second_term)

    J = J / m
    #加上正则化项
    J += (lamda/(2*m))*(np.power(theta_1[:,1:],2).sum()+np.power(theta_2[:,1:],2).sum())   #不含θ_0项
    return J

data = loadmat('ex4data1.mat')  #加载数据

theta_data = loadmat('ex4weights.mat')  # 加载数据
# 初始化操作
input_size = 400    #输入层
hidden_size = 25    #隐藏层
num_labels = 10     #输出层

theta_1 = theta_data.get('Theta1')
theta_2 = theta_data.get('Theta2')
theta_param = np.concatenate([np.ravel(theta_1),np.ravel(theta_2)])

1.当我们设置lamda为0，不含正则化时：

print(cost(theta_param,input_size,hidden_size,num_labels,X,y_onehot,0))

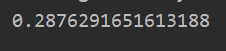
2.当设置lamda为1时：

print(cost(theta_param,input_size,hidden_size,num_labels,X,y_onehot,1))

（八）反向传播 了解

1.输入层不需要计算误差

2.输出层不需要计算sigmoid函数偏导：

3.其它层，我们需要以下计算：

（九）sigmoid函数求导

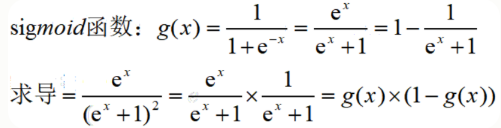
def sigmoid_gradient(z):
    return sigmoid(z)*(1-sigmoid(z))

（十）反向传播算法---计算误差、偏导

def backporp(theta_param,input_size,hidden_size,num_labels,X,y,lamda=1):
    # 获取样本个数
    m = X.shape[0]

    theta_1 = theta_param[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
    theta_2 = theta_param[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

    delta1 = np.zeros(theta_1.shape)  #由代价函数公式可以知道delta和theta是同型矩阵
    delta2 = np.zeros(theta_2.shape)

    # 先前向传播，将获得神经元单元激活值等信息
    a1, z2, a2, z3, h = forward_propagate(X, theta_1, theta_2)
    # 由于theta_2是（10，26）矩阵，所以d3i*theta_2是（1，26）矩阵，为了可以相乘，则我们要将z2加上一列
    z2 = np.insert(z2, 0, 1, axis=1)

    #求代价函数
    J = cost(theta_param,input_size,hidden_size,num_labels,X,y,lamda)

    #实现反向传播
    for i in range(m):
        a1i = a1[i,:]   #获取a1中得第i个
        z2i = z2[i,:]   #是（1，25）矩阵
        a2i = a2[i,:]
        hi = h[i,:]
        yi = y[i,:]

        #进行误差计算
        #先获取输出层3，的误差δ
        d3i = hi - yi   #是（1，10）矩阵
        d3i = np.array([d3i])
        #再获取隐藏层误差
        d2i = np.multiply((d3i@theta_2),np.array([sigmoid_gradient(z2i)]))  #(1,26)
        #获取各层误差
        delta1 = delta1 + (d2i[:,1:]).T*a1i  #获取第一层误差   (25,401)
        delta2 = delta2 + (d3i[:,:]).T*a2i  #获取第二层误差   (10,26)

    delta1 = delta1 / m
    delta2 = delta2 / m

    #加入正则化操作    注意：我们这里不包含δ_0
    delta1[:,1:] = delta1[:,1:] + (theta_1[:,1:]*lamda) / m
    delta2[:,1:] = delta2[:,1:] + (theta_2[:,1:]*lamda) / m

    #将梯度矩阵转化为单个数组
    grad = np.concatenate([np.ravel(delta1),np.ravel(delta2)])
    return J,grad

J,grad = backporp(theta_param,X,y_onehot,1)

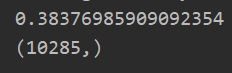
（十一） 预测函数

def predict_new(theta1,theta2,X):
    X = np.insert(X,0,1,axis=1)    #插入一列全为1的列向量到X中
    h_1 = sigmoid(X@theta1.T)
    h_1 = np.insert(h_1,0,1,axis=1)
    h_2 = sigmoid(h_1@theta2.T)

    p = np.argmax(h_2,axis=1)+1
    return p

#保证输入theta_param时一个向量，而不是矩阵。并且返回的梯度向量同theta_param同纬度---重点
fmin = minimize(fun=backporp,x0=theta_param,args=(input_size,hidden_size,num_labels,X,y_onehot,1),method='TNC',jac=True,options={'maxiter':250})

theta_param_new = fmin.x
theta_1_new = theta_param_new[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
theta_2_new = theta_param_new[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

y_pred = predict_new(theta_1_new,theta_2_new,X)
correct = [1 if a==b else 0 for (a,b) in zip(y_pred,y)] #重点：将预测值和原始值进行对比
accuracy = (sum(map(int,correct))/float(len(correct)))  #找到预测正确的数据/所有数据==百分比
print('accuracy = {0}%'.format(accuracy*100 ))

（十二）全部代码 

import math

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat    #用于载入matlab文件
import scipy.optimize as opt
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder #预处理操作

def displayData(X,example_width=None):  #显示20x20像素数据在一个格子里面
    if example_width is None:
        example_width = math.floor(math.sqrt(X.shape[1]))   #X.shape[1]=400
    print(X.shape)
    #计算行列
    m,n = X.shape   #返回的是我们随机选取的100行样本---（100，400）

    #获取图像高度
    example_height = math.ceil(n/example_width) #400/20 = 20

    # 计算需要展示的图片数量
    display_rows = math.floor(math.sqrt(m)) #10
    display_cols = math.ceil(m / display_rows)  #100/10=10

    fig,ax = plt.subplots(nrows=display_rows,ncols=display_cols,sharey=True,sharex=True,figsize=(12,12)) #https://blog.csdn.net/qq_39622065/article/details/82909421

    #拷贝图像到子区域进行展示
    for row in range(display_rows):
        for col in range(display_cols):
            ax[row,col].matshow(X[display_rows*row+col].reshape(example_width,example_height),cmap='gray') #希望将矩阵以图形方式显示https://www.cnblogs.com/shanger/articles/11872437.html

    plt.xticks([])  #用于设置每个小区域坐标轴刻度，设置为空，则不显示刻度
    plt.yticks([])

    plt.show()

def sigmoid(z):  # 实现sigmoid函数
    return 1 / (1 + np.exp(-z))

def one_to_all(X,y,num_labels,learning_rate):   #分类器构建  X训练集 y标签值 num_labels是构建的分类器数量（0-9标签值，则10个），learning_rate是入值
    rows = X.shape[0]
    cols = X.shape[1]

    #构建多维度θ值
    all_theta = np.zeros((num_labels,cols+1))   #这里我们需要添加θ_0,相应的我们要在X训练集中加入一列全为1的列向量

    #为X训练集添加一个全为1的列向量
    X = np.insert(X,0,values=np.ones(rows),axis=1)   #第二个参数是插入索引位置，第三个是插入数据，axis=1是列插入https://www.cnblogs.com/hellcat/p/7422005.html#_label2_9

    #开始进行参数拟合
    for i in range(1,num_labels+1):  #从1-10代替0-9，因为数据集的标签值是从1-10，print(np.unique(data['y']))可以知道
        theta = np.zeros(cols+1)    #初始化一个新的临时的θ值
        y_i = np.array([1 if label == i else 0 for label in y]) #进行二分类，对于对应的数设置为1，其他为0
        y_i = np.reshape(y_i,(rows,1))  #进行转置为列向量

        #使用高级优化算法进行参数迭代
        fmin = opt.minimize(fun=regularized_cost,x0=theta,args=(X, y_i),
                            method='TNC',jac=regularized_gradient)
        all_theta[i-1,:]=fmin.x #将1-10变为0-9

    return all_theta    #返回多维度θ值

def forward_propagate(X, theta1, theta2):   #X是我们输入层训练集，theta1是我们第一层的参数，theta2是我们的第二层参数
    #首先，我们要为输入数据集X，添加偏置单元
    a1 = np.insert(X,0,1,axis=1)    #插入一列全为1的列向量到X中
    #计算第二层激活值
    z2 = a1@theta1.T    #theta1是一个(25，401)矩阵，a1是（5000，401）---z2是（5000，25）
    a2 = np.insert(sigmoid(z2),0,1,axis=1)   #.之后添加偏置单元。变为（5000，26）
    #计算第三层激活值
    z3 = a2@theta2.T    #theta2是一个（10，26）矩阵，a2是（5000，26），所以z3是一个（5000，10）矩阵
    h = sigmoid(z3) #获取假设函数值

    return a1,z2,a2,z3,h

def cost(theta_param,X,y,lamda=1):  #lamda是正则化参数
    #获取样本个数
    m = X.shape[0]

    theta_1 = theta_param[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
    theta_2 = theta_param[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

    #将获得神经元单元激活值等信息
    a1,z2,a2,z3,h = forward_propagate(X,theta_1,theta_2)
    #初始化代价函数
    J = 0

    #根据公式计算代价函数
    for i in range(m):  #遍历每一个样本---m
        first_term = np.multiply(-y[i,:],np.log(h[i,:]))    #标签向量，乘以假设函数矩阵---K
        second_term = np.multiply((1-y[i,:]),np.log(1-h[i,:]))
        J += np.sum(first_term-second_term)

    J = J / m
    #加上正则化项
    J += (lamda/(2*m))*(np.power(theta_1[:,1:],2).sum()+np.power(theta_2[:,1:],2).sum())   #不含θ_0项
    return J

def sigmoid_gradient(z):
    return sigmoid(z)*(1-sigmoid(z))

def backporp(theta_param,X,y,lamda=1):
    # 获取样本个数
    m = X.shape[0]

    theta_1 = theta_param[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
    theta_2 = theta_param[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

    delta1 = np.zeros(theta_1.shape)  #由代价函数公式可以知道delta和theta是同型矩阵
    delta2 = np.zeros(theta_2.shape)

    # 先前向传播，将获得神经元单元激活值等信息
    a1, z2, a2, z3, h = forward_propagate(X, theta_1, theta_2)
    # 由于theta_2是（10，26）矩阵，所以d3i*theta_2是（1，26）矩阵，为了可以相乘，则我们要将z2加上一列
    z2 = np.insert(z2, 0, 1, axis=1)

    #求代价函数
    J = cost(theta_param,X,y,lamda)

    #实现反向传播
    for i in range(m):
        a1i = a1[i,:]   #获取a1中得第i个
        z2i = z2[i,:]   #是（1，25）矩阵
        a2i = a2[i,:]
        hi = h[i,:]
        yi = y[i,:]

        #进行误差计算
        #先获取输出层3，的误差δ
        d3i = hi - yi   #是（1，10）矩阵
        d3i = np.array([d3i])
        #再获取隐藏层误差
        d2i = np.multiply((d3i@theta_2),np.array([sigmoid_gradient(z2i)]))  #(1,26)
        #获取各层误差
        delta1 = delta1 + (d2i[:,1:]).T*a1i  #获取第一层误差   (25,401)
        delta2 = delta2 + (d3i[:,:]).T*a2i  #获取第二层误差   (10,26)

    delta1 = delta1 / m
    delta2 = delta2 / m

    #加入正则化操作    注意：我们这里不包含δ_0
    delta1[:,1:] = delta1[:,1:] + (theta_1[:,1:]*lamda) / m
    delta2[:,1:] = delta2[:,1:] + (theta_2[:,1:]*lamda) / m

    #将梯度矩阵转化为单个数组
    grad = np.concatenate([np.ravel(delta1),np.ravel(delta2)])
    return J,grad

def predict_new(theta1,theta2,X):
    X = np.insert(X,0,1,axis=1)    #插入一列全为1的列向量到X中
    h_1 = sigmoid(X@theta1.T)
    h_1 = np.insert(h_1,0,1,axis=1)
    h_2 = sigmoid(h_1@theta2.T)

    p = np.argmax(h_2,axis=1)+1
    return p

data = loadmat('ex4data1.mat')  #加载数据

theta_data = loadmat('ex4weights.mat')  # 加载数据
# 初始化操作
input_size = 400    #输入层
hidden_size = 25    #隐藏层
num_labels = 10     #输出层

theta_1 = theta_data.get('Theta1')
theta_2 = theta_data.get('Theta2')
theta_param = np.concatenate([np.ravel(theta_1),np.ravel(theta_2)])

X = data.get('X')
y = data.get('y')

encoder = OneHotEncoder(sparse=False)   #sparse=True 表示编码的格式，默认为 True，即为稀疏的格式，指定 False 则就不用 toarray() 了
y_onehot = encoder.fit_transform(y)

# J,grad = backporp(theta_param,X,y_onehot,1)
#保证输入theta_param时一个向量，而不是矩阵。并且返回的梯度向量同theta_param同纬度
fmin = minimize(fun=backporp,x0=theta_param,args=(X,y_onehot,1),method='TNC',jac=True,options={'maxiter':250})

theta_param_new = fmin.x
theta_1_new = theta_param_new[:(input_size + 1) * hidden_size].reshape(hidden_size, (input_size + 1))
theta_2_new = theta_param_new[(input_size + 1) * hidden_size:].reshape(num_labels, (hidden_size + 1))

y_pred = predict_new(theta_1_new,theta_2_new,X)
correct = [1 if a==b else 0 for (a,b) in zip(y_pred,y)] #重点：将预测值和原始值进行对比
accuracy = (sum(map(int,correct))/float(len(correct)))  #找到预测正确的数据/所有数据==百分比
print('accuracy = {0}%'.format(accuracy*100 ))