机器学习作业---逻辑回归（部分存疑）

一：建立一个逻辑回归模型来预测一个学生是否被大学录取。

假设你是一个大学系的管理员，你想根据两次考试的结果来决定每个申请人的录取机会。

你有以前的申请人的历史数据，你可以用它作为逻辑回归的训练集。

对于每一个培训例子，你有两个考试的申请人的分数和录取决定。

为了做到这一点，我们将建立一个分类模型，根据考试成绩估计入学概率。

 

（一）导入库，并且读取数据集

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

path = 'ex2data1.txt'
data = pd.read_csv(path,header=None,names=['exam1','exam2','admitted'])

print(data.head())　　#数据展示

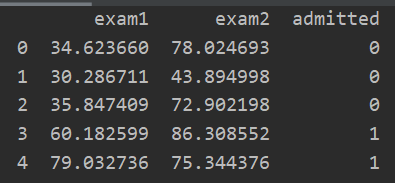
print(data.describe())　　#数据描述

（二）原始数据可视化

positive = data[data['admitted']==1]    #获取正样本
negative = data[data['admitted']==0]    #获取负样本

fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['exam1'],positive['exam2'],s=30,c='g',marker='o',label='Admitted')
ax.scatter(negative['exam1'],negative['exam2'],s=30,c='r',marker='x',label='Admitted')
ax.legend(loc=4)    #显示标签位置
ax.set_xlabel("Exam1 Score")
ax.set_ylabel("Exam2 Score")

plt.show()

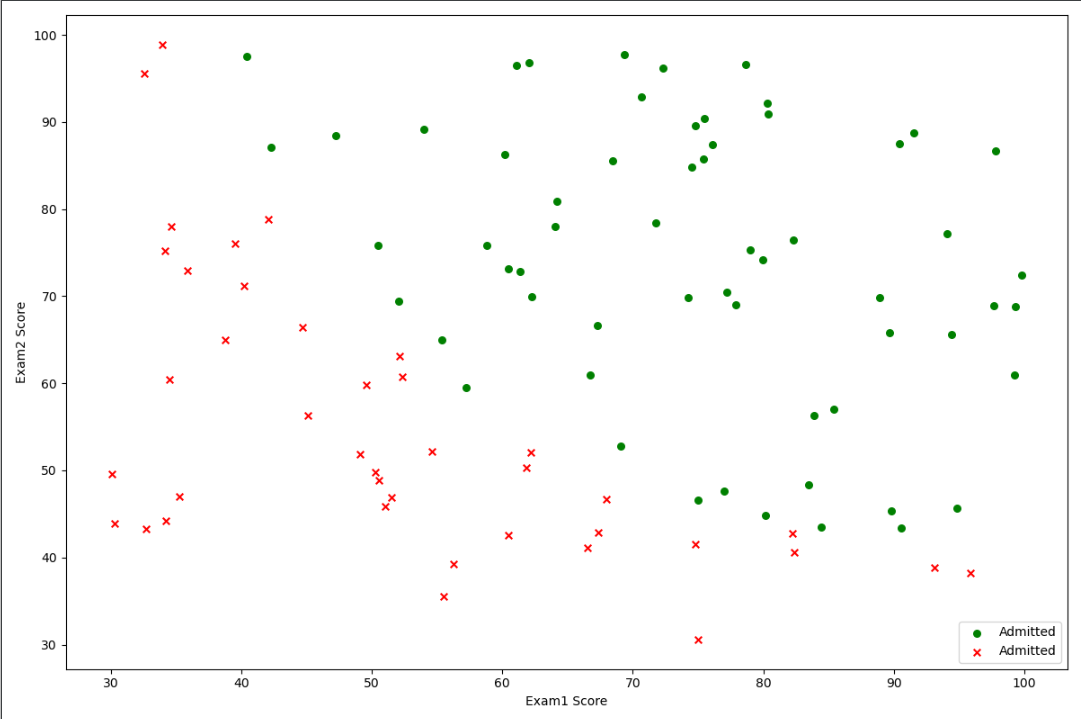
（三）数据预处理

在训练模型之前经常要对数据进行数组转化
当然很多时候在提取完数据后其自身就是数组形式（<class ‘numpy.ndarray’>），这只是习惯性的谨慎。很多时候取得的数据是DataFrame的形式，这个时候要记得转换成数组

def get_X(df):  #获取特征，并添加x_0列向量（全为1）
    ones = pd.DataFrame({'ones':np.ones(df.shape[0])})
    data = pd.concat([ones,df],axis=1)  #按axis=1列合并连接
    return data.iloc[:,:-1].as_matrix() #按相对位置，获取全部特征值数组    或者我们直接使用.values代替

def get_y(df):  #读取标签值
    return np.array(df.iloc[:,-1])  #这样可以转换为数组

def normalize_feature(df):  #进行归一化处理
    return  df.apply(lambda column:(column-column.mean())/column.std())#标准差标准化

X = get_X(data)
y = get_y(data)

print(data.head())
print(X)
print(y)

或者使用：

data = (data-data.mean())/data.std()

进行归一化。这里数据差距不大，所以不进行归一化。而且归一化，我们只对特征值进行处理，标签值可以不进行处理。

（四）实现sigmoid函数

def sigmoid(z): #实现sigmoid函数
    return 1/(1+np.exp(-z))

测试sigmoid函数，绘制图形：

fig,ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(-10,10,step=0.01),
        sigmoid(np.arange(-10,10,step=0.01)))　　#设置x,y轴各自数据，绘制图形
ax.set_xlabel('z',fontsize=18)
ax.set_ylabel('g(z)',fontsize=18)
ax.set_title('sigmoid function',fontsize=18)
plt.show()

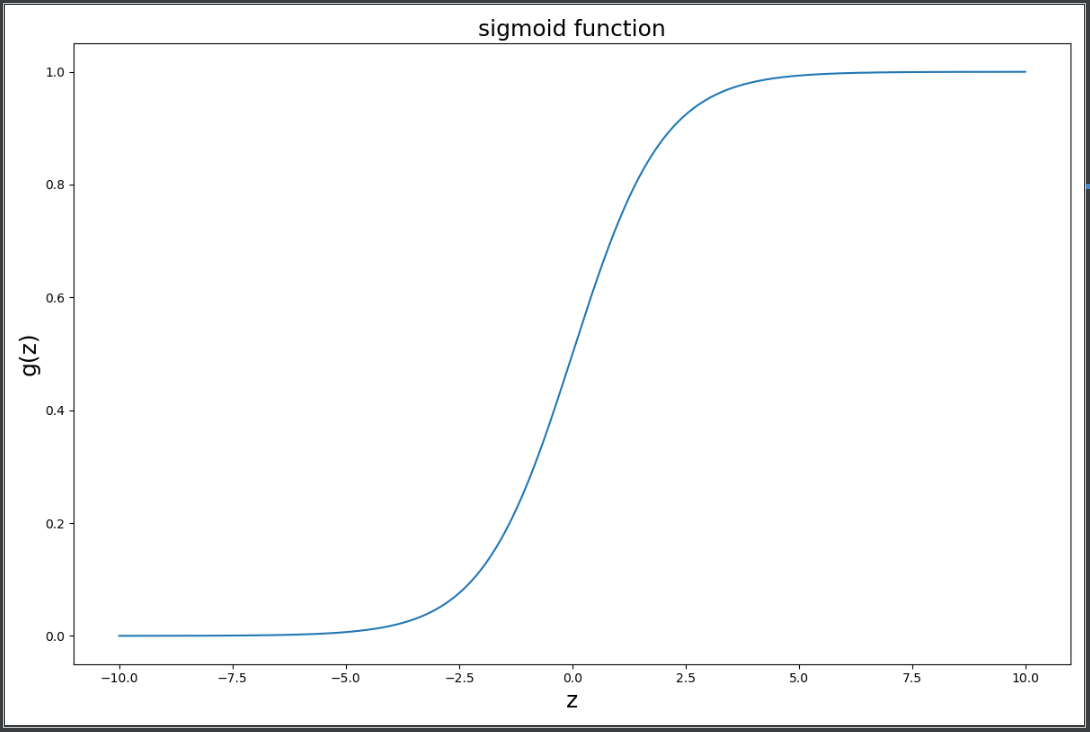
（五）实现代价函数

 

def cost(theta, X, y):
  　　theta = np.matrix(theta)
  　　X = np.matrix(X)
  　　y = np.matrix(y)
 　　 first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
 　　 second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
  　　return np.sum(first - second) / (len(X))

注意：我们要使用*实现矩阵乘法，那么我们必须使得两边参数类型为matrix类型

补充：numpy中的matrix矩阵处理---numpy似乎并不推荐使用matrix矩阵类型

对于上面的X*theta.T，我们使用了“*”运算符，进行了矩阵乘法操作。但是我们如果将*当作矩阵乘法，那么我们必须保证两边操作数类型是matrix矩阵类型。另外dot也可以实现矩阵乘法，但是它要求传参是ndarray类型，并且两个数组保持第一个矩阵列数等于第二个矩阵行数。

def cost(theta, X, y):  #实现代价函数　　----直接使用array类型
    first = np.multiply(-y, np.log(sigmoid(X.dot(theta.T))))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X.dot(theta.T))))
    return np.sum(first - second) / (len(X))

测试代价函数：

X = get_X(data)
y = get_y(data)
theta = np.zeros(X.shape[1])    #返回numpy.ndarray类型

print(cost(theta,X,y))

（六）梯度下降法

1.计算梯度：推导

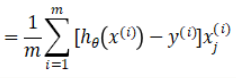
def gradient(theta,X,y):    #实现求梯度
    return X.T@(sigmoid(X@theta)-y)/len(X)

补充：numpy矩阵相乘matmul可以用@来代替

或者：

def gradient(theta,X,y):    #实现求梯度
    return (X.T).dot(np.array([(sigmoid(X.dot(theta.T))-y)]).T).flatten()/len(X)

补充：对于numpy.ndarray类型数据，如果要进行矩阵运算，那么数组必须是二维数组[[]]

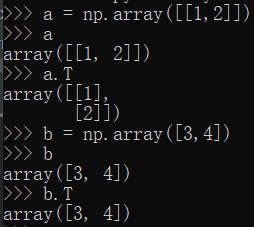
print(gradient(theta,X,y))

2.参数拟合---梯度下降法

def gradientDescennt(theta,X,y,alpha,iters):    #进行梯度下降法拟合参数
    costs = np.zeros(iters)
    temp = np.ones(len(theta))
    for i in range(iters):  #进行迭代
        temp = theta - alpha*gradient(theta,X,y)
        theta = temp
        costs[i] = cost(theta,X,y)
    return theta,costs

可视化操作：

theta,costs =gradientDescennt(theta,X,y,0.001,1000)　　#注意：这里我们选取的步长不易太大
print(theta)
print(costs[-1])
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(1000),costs,'r')
ax.set_xlabel("Iterations")
ax.set_ylabel("Cost")
ax.set_title("Error vs. Iteration")
plt.show()

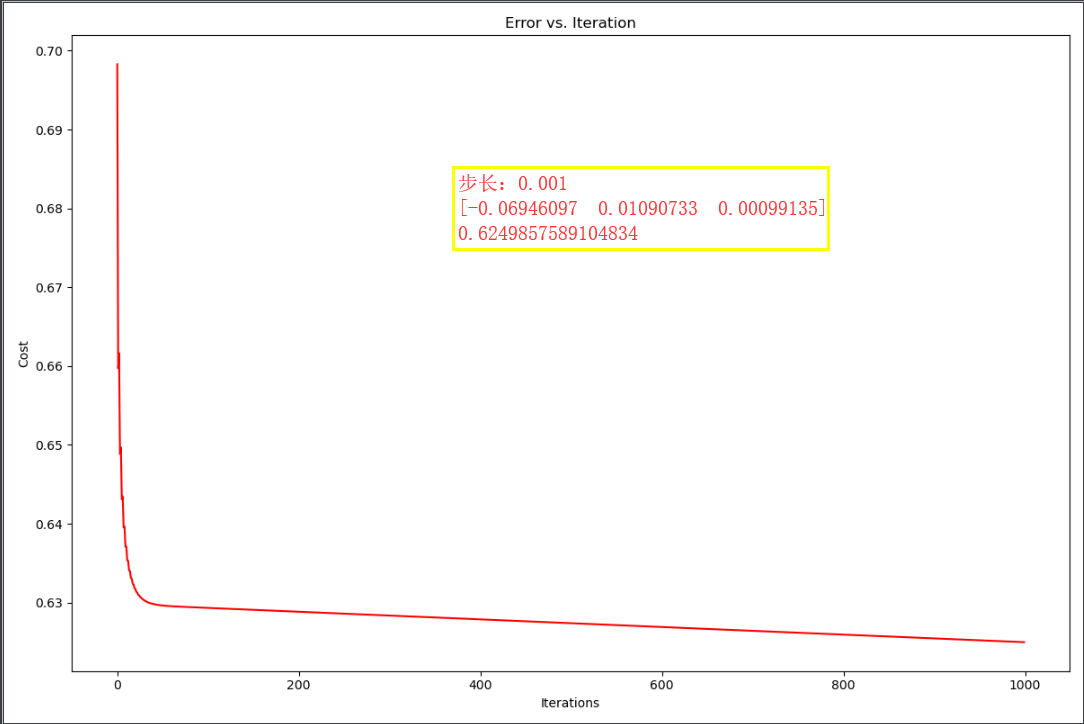
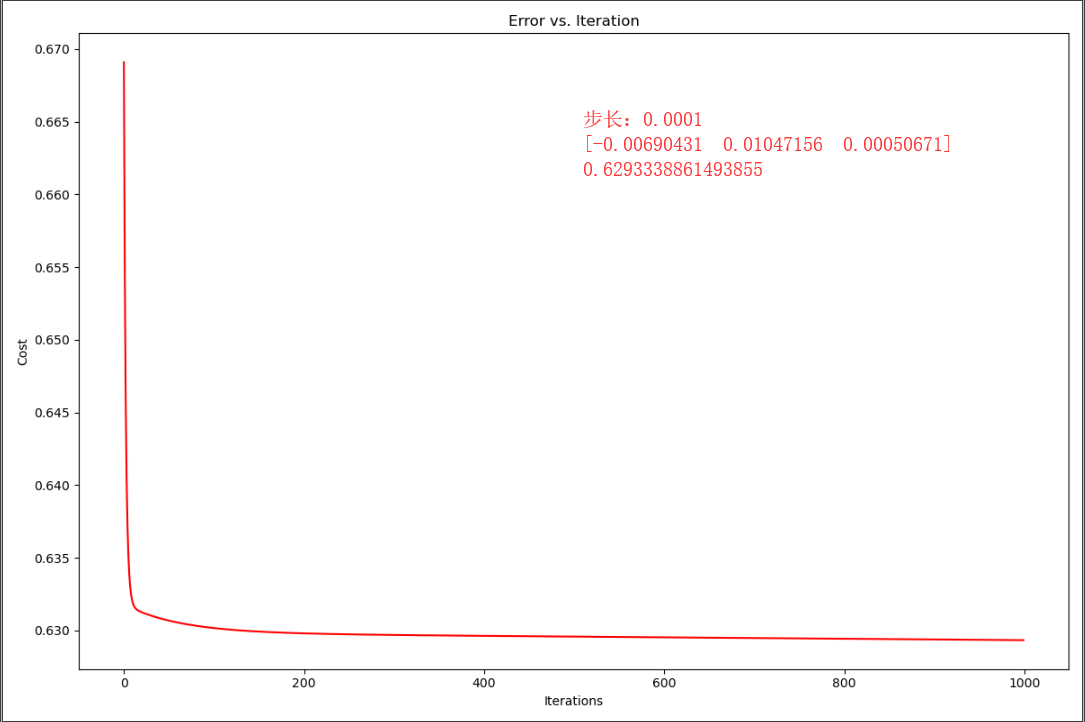
可以发现，当步长太大，导致代价值发散。

而且：梯度下降法得到的拟合参数。和下面高级优化算法参数不一致....决策边界也不对....???

难道是因为数据没有进行归一化处理？？ 

以后进行回顾补充！！！

3.参数拟合---高级优化算法

import scipy.optimize as opt　　#使用高级优化算法

res = opt.minimize(fun=cost,x0=theta,args=(X,y),jac=gradient,method='TNC')
print(res)

https://www.cnblogs.com/tongtong123/p/10634716.html

其中：x就是我们要的θ值

根据训练的模型参数对数据进行预测:

def predict(X,theta):   #对数据进行预测
    return (sigmoid(X @ theta.T)>=0.5).astype(int)  #实现变量类型转换

res = opt.minimize(fun=cost,x0=theta,args=(X,y),jac=gradient,method='TNC')
theta_res = res.x   #获取拟合的θ参数

y_pred = predict(X,theta_res)
print(classification_report(y,y_pred))

 

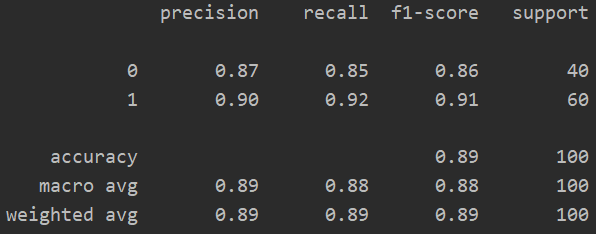
（七）可视化决策边界

这里已经得到了θ的参数，将Xθ取0即可得到对应的决策边界函数。

#先绘制原来数据
positive = data[data['admitted'] == 1]   # 挑选出录取的数据
negative = data[data['admitted'] == 0]   # 挑选出未被录取的数据
fig, ax = plt.subplots(figsize=(10, 5))      # 获取绘图对象
# 对录取的数据根据两次考试成绩绘制散点图
ax.scatter(positive['exam1'], positive['exam2'], s=30, c='b', marker='o', label='Admitted')
# 对未被录取的数据根据两次考试成绩绘制散点图
ax.scatter(negative['exam1'], negative['exam2'], s=30, c='r', marker='x', label='Not Admitted')
# 添加图例
ax.legend()
# 设置x,y轴的名称
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.title("fitted curve vs sample")

#绘制决策边界
print(theta_res)
exam_x = np.arange(X[:,1].min(),X[:,1].max(),0.01)
theta_res = - theta_res/theta_res[2]  #获取函数系数θ_0/θ_2 θ_0/θ_2
print(theta_res)
exam_y = theta_res[0]+theta_res[1]*exam_x
plt.plot(exam_x,exam_y)
plt.show()

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import classification_report
import scipy.optimize as opt

def get_X(df):  #获取特征，并添加x_0列向量（全为1）
    ones = pd.DataFrame({'ones':np.ones(df.shape[0])})
    data = pd.concat([ones,df],axis=1)  #按axis=1列合并连接
    return data.iloc[:,:-1].values #按相对位置，获取全部特征值数组

def get_y(df):  #读取标签值
    return np.array(df.iloc[:,-1])  #这样可以转换为数组

def normalize_feature(df):  #进行归一化处理
    return df.apply(lambda column: (column-column.mean())/column.std())#标准差标准化

def sigmoid(z): #实现sigmoid函数
    return 1/(1+np.exp(-z))

def cost(theta, X, y):  #实现代价函数
    first = np.multiply(-y, np.log(sigmoid(X.dot(theta.T))))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X.dot(theta.T))))
    return np.sum(first - second) / (len(X))

def gradient(theta,X,y):    #实现求梯度
    return X.T@(sigmoid(X@theta)-y)/len(X)

def gradientDescennt(theta,X,y,alpha,iters):    #进行梯度下降法拟合参数
    costs = np.zeros(iters)
    temp = np.ones(len(theta))
    for i in range(iters):  #进行迭代
        temp = theta - alpha*gradient(theta,X,y)
        theta = temp
        costs[i] = cost(theta,X,y)
    return theta,costs

def predict(X,theta):   #对数据进行预测
    return (sigmoid(X @ theta.T)>=0.5).astype(int)  #实现变量类型转换

path = 'ex2data1.txt'
data = pd.read_csv(path,header=None,names=['exam1','exam2','admitted'])

X = get_X(data)
y = get_y(data)
theta = np.zeros(X.shape[1])    #返回numpy.ndarray类型

res = opt.minimize(fun=cost,x0=theta,args=(X,y),jac=gradient,method='TNC')
theta_res = res.x   #获取拟合的θ参数
#theta_res,costs =gradientDescennt(theta,X,y,0.00001,500000)

#先绘制原来数据
positive = data[data['admitted'] == 1]   # 挑选出录取的数据
negative = data[data['admitted'] == 0]   # 挑选出未被录取的数据
fig, ax = plt.subplots(figsize=(10, 5))      # 获取绘图对象
# 对录取的数据根据两次考试成绩绘制散点图
ax.scatter(positive['exam1'], positive['exam2'], s=30, c='b', marker='o', label='Admitted')
# 对未被录取的数据根据两次考试成绩绘制散点图
ax.scatter(negative['exam1'], negative['exam2'], s=30, c='r', marker='x', label='Not Admitted')
# 添加图例
ax.legend()
# 设置x,y轴的名称
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.title("fitted curve vs sample")

#绘制决策边界
print(theta_res)
exam_x = np.arange(X[:,1].min(),X[:,1].max(),0.01)
theta_res = - theta_res/theta_res[2]  #获取函数系数θ_0/θ_2 θ_0/θ_2
print(theta_res)
exam_y = theta_res[0]+theta_res[1]*exam_x
plt.plot(exam_x,exam_y)
plt.show()

二：正则化逻辑回归

0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0

（一）数据读取和展示

path = 'ex2data2.txt'
data = pd.read_csv(path,header=None,names=['test1','test2','accepted'])

#先绘制原来数据
positive = data[data['accepted'] == 1]   # 挑选出录取的数据
negative = data[data['accepted'] == 0]   # 挑选出未被录取的数据
fig, ax = plt.subplots(figsize=(10, 5))      # 获取绘图对象
# 对录取的数据根据两次考试成绩绘制散点图
ax.scatter(positive['test1'], positive['test2'], s=30, c='b', marker='o', label='Accepted')
# 对未被录取的数据根据两次考试成绩绘制散点图
ax.scatter(negative['test1'], negative['test2'], s=30, c='r', marker='x', label='Not Accepted')
# 添加图例
ax.legend()
# 设置x,y轴的名称
ax.set_xlabel('test1')
ax.set_ylabel('test2')
plt.title("fitted curve vs sample")
plt.show()

（二）特征映射

对于较复杂的边界，我们需要使用多项式来表示，所以，我们需要通过特征映射，来找到合适的多项式。

其中i决定了最高次项。

主要功能，是将原来的2个特征值（不含accepted),变为新的28为多项式特征值。----n(n+1)/2其中n等于7（从0到x^6)

def feature_mapping(x,y,power,as_ndarray=False):
    data = {"f{}{}".format(i - p, p): np.power(x, i - p) * np.power(y, p)
            for i in np.arange(power+1)
            for p in np.arange(i+1)}
    if as_ndarray:
        return pd.DataFrame(data).as_matrix()
    else:
        return pd.DataFrame(data)

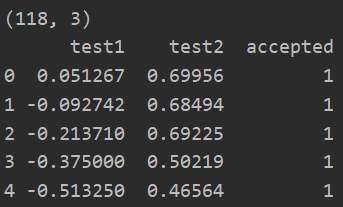
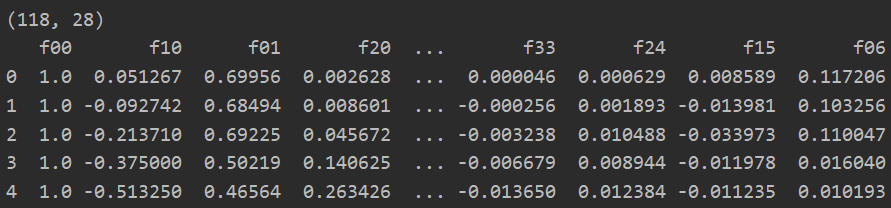
path = 'ex2data2.txt'
data = pd.read_csv(path,header=None,names=['test1','test2','accepted'])
print(data.shape)
print(data.head())

data = feature_mapping(np.array(data.test1),np.array(data.test2),power=6)
print(data.shape)
print(data.head())

（三）正则化代价函数

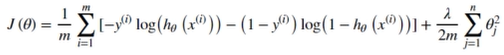
def regularized_cost(theta, X, y, learningRate=1):  #实现代价函数
    first = np.multiply(-y, np.log(sigmoid(X.dot(theta.T))))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X.dot(theta.T))))
    reg = (learningRate/(2*len(X)))*np.sum(np.power(theta[1:theta.shape[0]],2))
    return np.sum(first - second) / (len(X)) + reg

path = 'ex2data2.txt'
data = pd.read_csv(path,header=None,names=['test1','test2','accepted'])

X = feature_mapping(np.array(data.test1),np.array(data.test2),power=6)

#X = get_X(data)
y = get_y(data)
theta = np.zeros(X.shape[1])    #返回numpy.ndarray类型

print(regularized_cost(theta,X,y))

因为我们设置的θ为0，所以这个正则化代价函数与代价函数的值应该相同。 

（四）正则化梯度

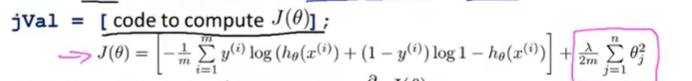
正则化不包含θ_0！！！

def gradient(theta,X,y):    #实现求梯度
    return X.T@(sigmoid(X@theta)-y)/len(X)

def regularized_gradient(theta,X,y,learningRate=1):
    theta_new = theta[1:]   #不加θ_0
    regularized_theta = (learningRate/len(X))*theta_new
    regularized_term = np.concatenate([np.array([0]),regularized_theta])    #前面加上0，是为了加给θ_0
    return gradient(theta,X,y)+regularized_term

path = 'ex2data2.txt'
data = pd.read_csv(path,header=None,names=['test1','test2','accepted'])
X = feature_mapping(np.array(data.test1),np.array(data.test2),power=6)
#X = get_X(data)
y = get_y(data)
theta = np.zeros(X.shape[1])    #返回numpy.ndarray类型

print(regularized_gradient(theta,X,y))

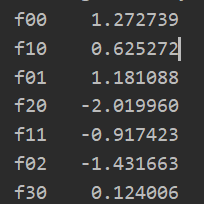
（五）高级优化算法拟合参数θ 

res = opt.minimize(fun=regularized_cost,x0=theta,args=(X,y),jac=regularized_gradient,method='Newton-CG')
print(res.x)

（六）画出决策边界

#先绘制原来数据
positive = data[data['accepted'] == 1]   # 挑选出录取的数据
negative = data[data['accepted'] == 0]   # 挑选出未被录取的数据
fig, ax = plt.subplots(figsize=(12, 8))      # 获取绘图对象
# 对录取的数据根据两次考试成绩绘制散点图
ax.scatter(positive['test1'], positive['test2'], s=30, c='b', marker='o', label='Accepted')
# 对未被录取的数据根据两次考试成绩绘制散点图
ax.scatter(negative['test1'], negative['test2'], s=30, c='r', marker='x', label='Not Accepted')
# 添加图例
ax.legend()
# 设置x,y轴的名称
ax.set_xlabel('test1')
ax.set_ylabel('test2')
plt.title("Regularized Logistic Regression")

#绘制决策边界
x = np.linspace(-1, 1.5, 250)
xx, yy = np.meshgrid(x, x)  #生成网格点坐标矩阵 https://blog.csdn.net/lllxxq141592654/article/details/81532855
z = feature_mapping(xx.ravel(), yy.ravel(), 6)  #xx,yy都是（250，250）矩阵，经过ravel后，全是(62500,1)矩阵。之后进行特征变换获取(62500,28)的矩阵
z = z @ theta_res   #将每一行多项式与系数θ相乘，获取每一行的值=θ_0+θ_1*X_1+...+θ_n*X_n
z = np.array([z]).reshape(xx.shape) #将最终值转成250行和250列坐标
print(z)
plt.contour(xx, yy, z, 0)   #传入的xx,yy需要同zz相同维度。
                            # 其实xx每一行都是相同的，yy每一列都是相同的，所以本质上来说xx是决定了横坐标，yy决定了纵坐标.
                            # 而z中的每一个坐标都是对于(x,y)的值---即轮廓高度。
                            # 第四个参数如果是int值，则是设置等高线条数为n+1---会自动选取最全面的等高线。　　如何选取等高线？具体原理还要考虑：是因为从所有数据中找到数据一样的点？
                            # https://blog.csdn.net/lanchunhui/article/details/70495353
                            # https://matplotlib.org/api/_as_gen/matplotlib.pyplot.contour.html#matplotlib.pyplot.contour
plt.show()

可以通过改变入的值，来调整参数。