机器学习基础---神经网络(属于逻辑回归)(构建训练集以及参数学习)
一:代价函数---为神经网络拟合参数
(一)神经网络字母概念
主要讲解神经网络在分类问题中的应用
假设我们有一个和下图类似的神经网络结构:

并且有一个像下面这样的训练集:其中有m组训练样本(x^i,y^i)

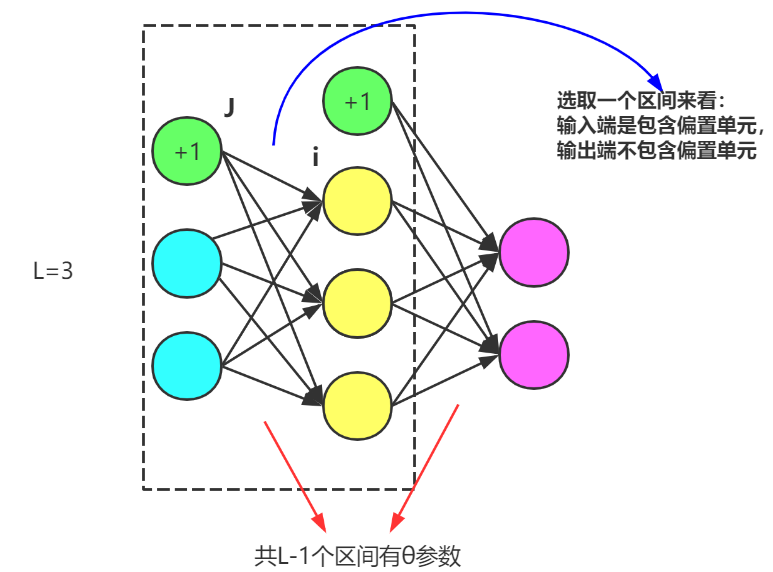
并且用大写字母L表示神经网络结构的总层数:

用sl表示第L层的单元数,也就是神经元的数量(不包含该层的偏差单元)

其中S_L表示输出层的单元数
(二)二分类和多分类

K表示输出层单元数(也是h(x)维数)。注意:二分类的K为1,多分类的K>=3(因为=2就是二分类)
(三)定义代价函数
我们在神经网络里,使用的代价函数,是逻辑回归里使用的代价函数的一般化形式:(含正则项)
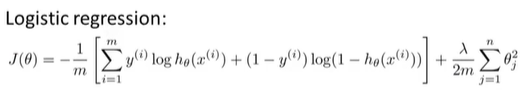
对于逻辑回归而言,我们通常使代价函数 J(θ)最小化。
对于一个神经网络来说,我们的代价函数是这个式子的一般化形式。
这里不再是仅有一个逻辑回归输出单元,取而代之的是K个,所以下面的是我们的代价函数:

神经网络现在输出了属于R^K的向量:
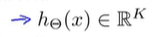
并用h(x)_i来表示第i个输出,也就是说h(x)是一个K维向量。下标 i 表示选择了神经网络输出向量的第i个元素。
神经网络的代价函数 J(θ) 将成为下面这样的形式:

这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出K个预测,基本上我们可以利用循环,对每一行特征都预测K个不同结果,然后在利用循环在K个预测中选择可能性最高的一个(m个之间<k个预测和>代价最小),将其与y中的实际数据进行比较。
正则化的那一项只是排除了每一层θ_0后,每一层的θ矩阵的和。最里层的循环j循环所有的行(由s_l+1 层的激活单元数决定),循环i则循环所有的列,由该层(s_l层)的激活单元数所决定。即:h_θ(x)与真实值之间的距离为每个样本-每个类输出的加和,对参数进行regularization的bias项处理所有参数的平方和。
第一项:∑关于K,是对K从1到K每一个预测维度的值进行求和。∑关于m是对每一行数据,都给出K个预测。
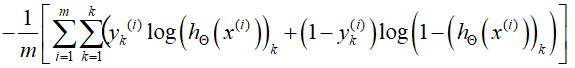
第二项:∑关于L-1,表示L层之间一共有L-1个区间有θ参数。∑关于S_L表示θ_ij组合中的输出端(不包含偏置单元)。∑关于S_L+1表示θ_ij组合中的输入端(含偏置单元)---默认不惩罚输出端偏置单元

二:优化代价函数---让其最小化的算法(反向传播算法)
(一)实现思路
代价函数如下:

目标是找到参数θ,实现代价函数最小化:
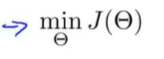
实现方法:为了使用梯度下降法或者其他高级优化算法,我们需要写这样一段代码:(求偏导)

(二)对比前向传播方法
假设我们的训练集只有一个实例(x^(1),y^(1)),我们的神经网络是一个四层的神经网络,其中K=4,S_L=4,L=4。

前向传播:---计算每一个神经元的激活值
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的h_θ(x)。
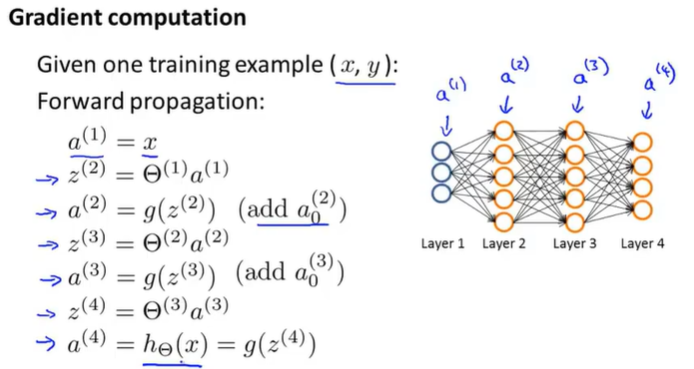
所以这里我们实现了把前向传播向量化,这使得我们可以计算神经网络结构里的每一个神经元的激活值。

前向传播:需要加上偏置单元
反向传播:---计算每个节点误差
现在,为了计算代价函数的偏导数:
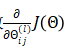
我们需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。 以一个例子来说明反向传播算法。

反向传播:不需要偏置单元
前向传播,由前向后用于计算出每个神经元的激活值。 反向传播,由后向前,需要用到前向传播的激活值来计算神经元节点的误差。
(三)反向传播算法
反向传播算法从直观上来说,我们计算这样一个值:δj(l)-----表示第l层第j个节点的误差
回顾一下:aj(l)-----表示第l层第j个节点的激活值
所以:这个δ项在某种程度上,就捕捉到了我们在这个神经节点的激活值的误差
所以: 我们希望这个节点的激活值稍微不一样
反向传播法这个名字:源于我们从输出层开始计算δ项。然后我们返回到上一层计算第三隐藏层的δ项。接着我们再往前一步来计算δ(2)。所以说我们是类似于把输出层的误差反向传播给了第3层,然后是再传到第二层,这就是反向传播的意思。

(四)误差求解

该图不包含偏置单元。
补充:

1.对于L=4 (第四层输出层)
![]()
对于每一个输出单元,我们将计算δ项,等于这个单元的激活值减去训练样本里的真实值。
对于输出层,我们的aj(4)=(hθ(x))j
向量化表达式:
![]()
这里每一个值都是一个向量 ,其维度等于输出单元的数目。
2.第3层的误差项
![]()
其中θ(3)是一个4*5矩阵(反向传播不含偏置单元),δ(4)是一个4维列向量(由1可以知道),“.*“表示点乘。g`(z(3))也是一个向量:
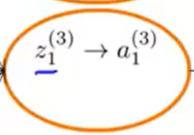
其中z是输入,a是sigmoid函数输出。
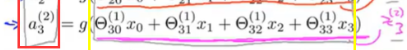
对sigmoid函数求导:(只是标量求导)
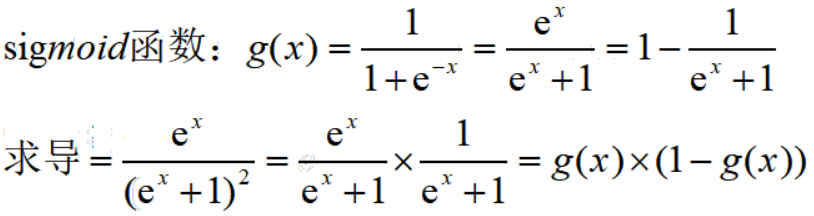
![]()
其中a(3)的维度是第3层神经元单元个数。---是一个5维向量
所以g`(z(3))=a(3).*(1-a(3))注意:这里是向量求导,结果是点乘。另外1也是一个向量
a.*b表示矩阵a中的元素与矩阵b中的元素按照相同位置进行相乘,得到的结果作为新矩阵中相同位置的元素。
以上可以知道:
θ(3)是一个4*5矩阵
θ(3)T是一个5*4矩阵
δ(4)是一个4维列向量
所以:![]() 是一个5维列向量
是一个5维列向量
又因为:
![]()
所以![]() 是一个5维列向量
是一个5维列向量
因此:![]() 还是一个5维列向量
还是一个5维列向量
3.第2层的误差项
![]()
θ(2)是一个5*5矩阵
θ(2)T是一个5*5矩阵
δ(3)是一个5维列向量
g`(z(2))=a(2).*(1-a(2))是一个5维列向量
所以:δ(2)也是一个5维列向量
4.因为第一层是输入变量,不存在误差。所以不进行计算
总之:我们有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设入=0,即我们不做任何正则化处理时有:
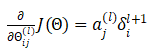
l代表目前所计算的是第几层。
j代表目前计算层中的激活单元的下标,也将是下一层的第个输入变量的下标。
i代表下一层中误差单元的下标,是受到权重矩阵中第行影响的下一层中的误差单元的下标。
如果我们考虑正则化处理,并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中,我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中,我们同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵,我们用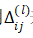 来表示这个误差矩阵。第l层的第i个激活单元受到第j个参数影响而导致的误差。
来表示这个误差矩阵。第l层的第i个激活单元受到第j个参数影响而导致的误差。
(五)算法实现
当我们有一个很大的训练集,我们的算法表示为:

即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出了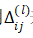 之后,我们便可以计算代价函数的偏导数了,计算方法如下:
之后,我们便可以计算代价函数的偏导数了,计算方法如下:

(六)总结
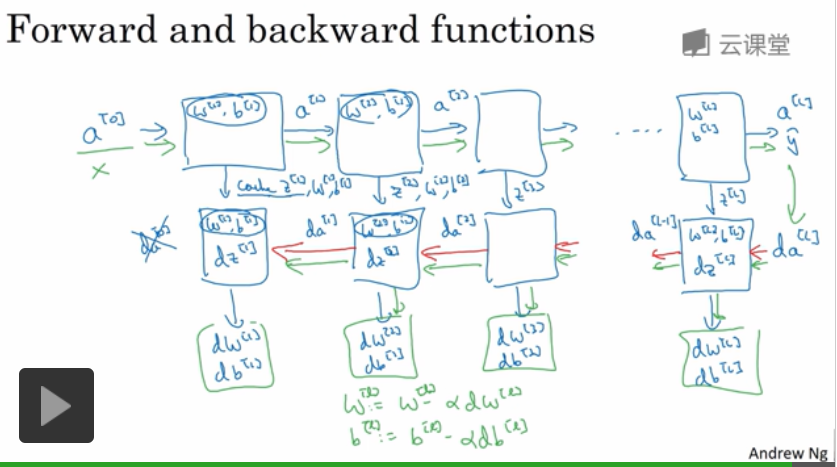
在前向传播中,我们根据权重θ<即图中w,b>计算出激活项值a,并进行缓存本轮权重和激活项值。

在反向传播中,我们计算所有误差项,从而获得权重的导数,从而对整体权重进行梯度下降操作。
注意:在反向传播中,我们的导数求解使用链式法则进行:


上面求解都是按照链式法则进行的。
总结:
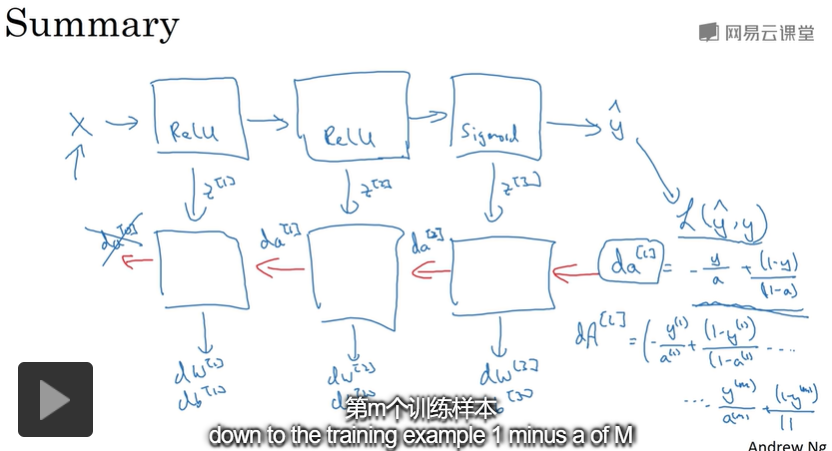
注意:上面对da[l]求导时,是基于逻辑回归求解的。

这里我们的预测值就是a,所以y^=a,我们对a的求导结果是:

三:反向传播理解
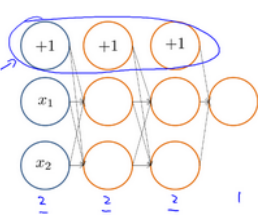
(一)前向传播过程
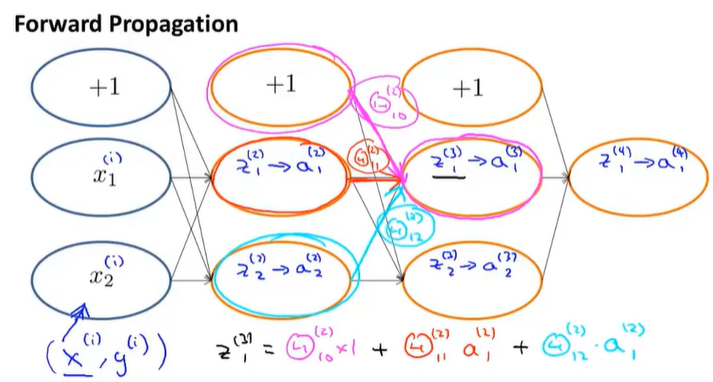
(二)反向传播过程

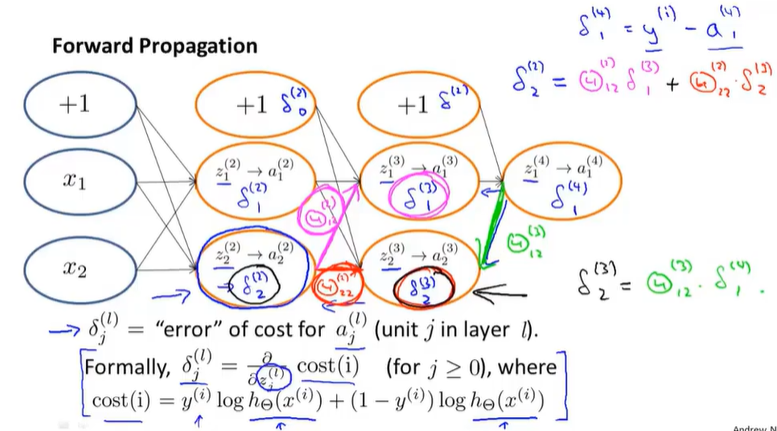
作者:山上有风景
欢迎任何形式的转载,但请务必注明出处。
限于本人水平,如果文章和代码有表述不当之处,还请不吝赐教。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
2019-05-03 算法习题---3.01猜数字游戏提示(UVa340)