机器学习基础---神经网络(属于逻辑回归)(构建假设函数)
一:为什么需要神经网络
(一)案例

为了很好的拟合数据,我们需要保留较多的相关参数,虽然可以使用正则化进行优化。但是无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。
之前我们已经看到过,使用非线性的多项式项,能够帮助我们建立更好的分类模型。假设我们有非常多的特征,例如大于100个变量。
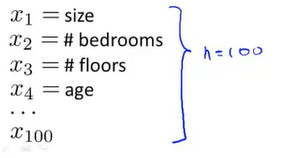
我们希望用这100个特征来构建一个非线性的多项式模型,结果将是数量非常惊人的特征组合,即便我们只采用两两特征的组合:
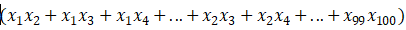
我们也会有接近5000个组合而成的特征。
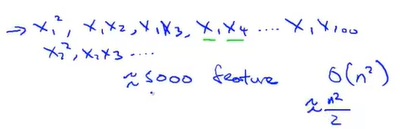
这对于一般的逻辑回归来说需要计算的特征太多了。所以,当特征个数n很大时(许多实际的机器学习问题特征都是很大的),将这些高阶多项式项数包含到特征里面,会导致特征空间急剧膨胀。
(二)案例二:计算机视觉
假设我们希望训练一个模型来识别视觉对象(例如识别一张图片上是否是一辆汽车),我们怎样才能这么做呢?

假设使用机器学习算法,来训练一个分类器,使它检测一个图像,来判断图像是否为一辆汽车。
我们取出这幅图片中的一小部分,将其放大:

当人眼看到一辆汽车时,计算机实际上看到的却是这个:一个数据矩阵,表示了像素强度值
因此,对于计算机视觉来说问题就变成了:根据这个像素点亮度矩阵,来告诉我们,这些数值代表一个汽车门把手。
具体而言,当用机器学习算法构造一个汽车识别器时,我们要做的就是提供一个带标签的样本集

将这个样本集输入给学习算法,以训练出一个分类器,然后我们进行测试,输入一副新的图片,让分类器判定这是什么东西。理想情况下,分类器可以识别出这是一辆汽车。
(三) 引入非线性假设的必要性
从学习算法的训练样本中,挑出一些汽车图片和一些非汽车图片
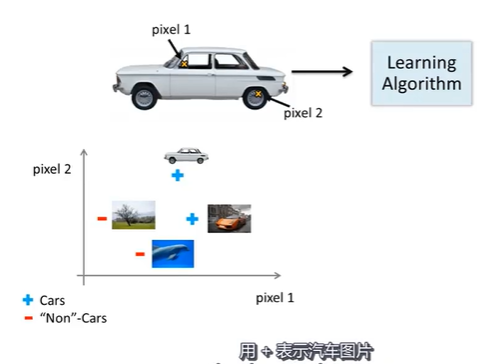
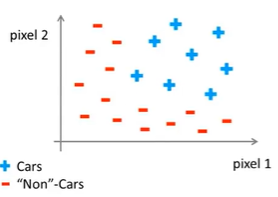
让我们从其中每幅图片中挑出一组像素点,分别是上面的像素点1和像素点2的位置。

但上面依然是2500个像素点。因此特征向量的数量是N=2500,特征向量x就是所有像素强度的列表。
包括像素点1和像素点2的亮度等等,直到最后一个像素点的亮度。
如果是灰度图片,那么每个像素点的值应该是0-255。如果是RGB图像,那么n=7500
如果我们要通过包含所有的二次项特征,来学习得到非线性假设,那么这就是式子中的所有条件x_i*x_j约等于300万个特征----计算成本过高
神经网络:他在学习复杂的非线性假设上被证明是一种好得多的算法。即使你输入特征空间或输入的特征维数n很大也能轻松搞定。
二:神经网络的表示---假设函数h(X)
运用神经网络时,我们该如何表示我们的假设或模型
(一)神经元模型
神经元比喻模型:神经网络是在模仿大脑中的神经元或者神经网络时发明的。
因此,要解释如何表示模型假设,我们先来看单个神经元在大脑中如何工作。
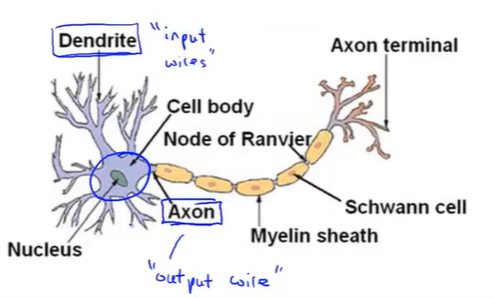
神经元是一个计算单元
1.是神经元有细胞主体
2.是神经元有一定数量的输入神经,这些输入神经叫做树突。它们接收来自其他神经元的信息。
3.神经元有一条输出神经,叫做轴突,这些输出神经是用来给其他神经元传递信号或者传送信息的
(二)如何表示假设---单个神经元
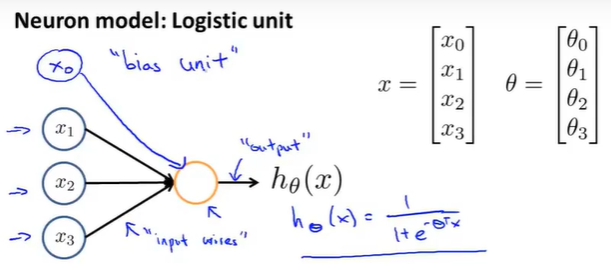
其中x_0被称为偏置单元,总是为1。
θ是参数,也可以叫做模型的权重。
上图是一个神经元。
(三)神经网络-----一组神经元

x_i为输入单元,同样可以画出x_0
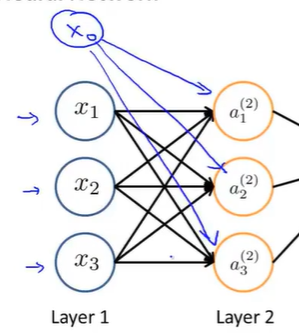
a_j是神经元,这里有3个这样的神经元。---也可以添加a_0为偏置单元
其中第3层神经元进行输出:

总之:
第一层为输入层,输入特征x_i。
第二层为隐藏层(不止一个),在监督学习中,可以看到输入,也可以看到正确的输出,而隐藏层的值,在训练集中是看不到的。
最后一层为输出层,它输出假设的最终计算结果
(四)神经网络计算步骤


激活项(单元):由一个具体神经元计算并输出的值

我们的神经网络,被这些矩阵参数化。θ_j就是权重矩阵,它控制从某一层,比如说从第一层到第二层或者第二层到第三层的作用。
所以,对于上图所示的模型,所表示的计算:
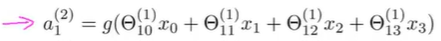
上面是第一个隐藏单元是按照上面进行计算它的值的。同样第二三相同:

其中θ_1就是控制着从三个输入单元到三个隐藏单元(还要包含一个偏置单元,所以实际是4个)的映射的参数矩阵。
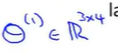
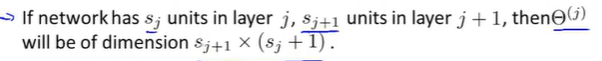
注意:其中下标θ_ij表示的是:i同前面α下标一致,表示输出位置。j为前面输入位置。
最后在输出层,我们还有一个单元(可以写成![]() ),负责计算h(x):
),负责计算h(x):

(五)高效计算和一个向量化的实现方法
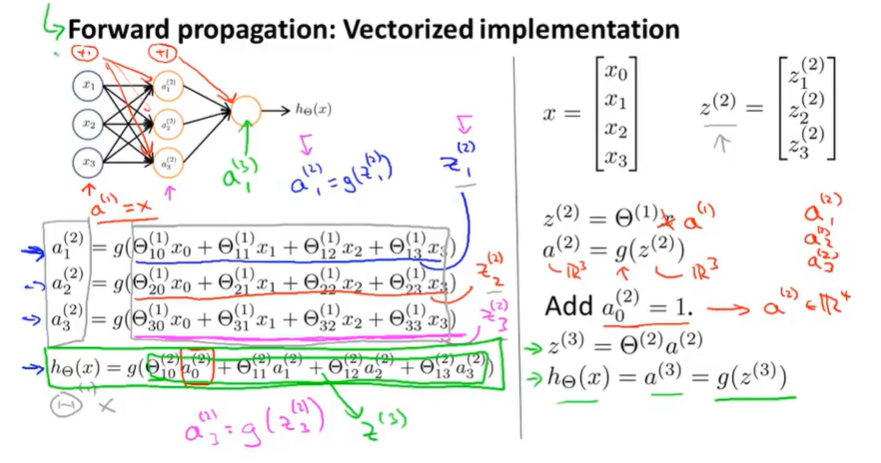
前向传播相对于使用循环来编码,利用向量化的方法会使得计算更为简便。以上面的神经网络为例,试着计算第二层的值:


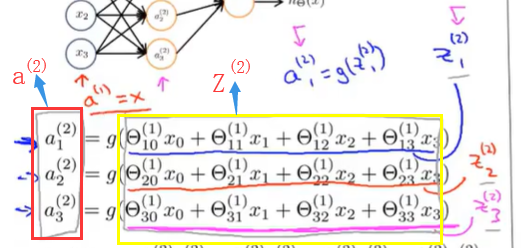
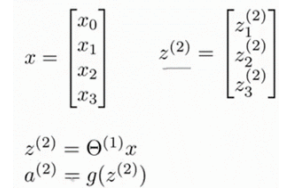

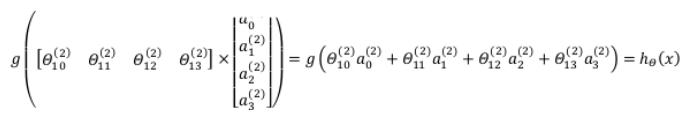


这个计算h(x)的过程,就是前向传播。这样命名是因为我们从输入层的激励(激活项)开始,然后进行前向传播给隐藏层并计算隐藏层的激励,然后我们继续前向传播并计算输出层的激励。
这个从输入层到隐藏层再到输出层依次计算激励的过程叫前向传播。
我们刚刚得到了这一过程的向量化实现方法:
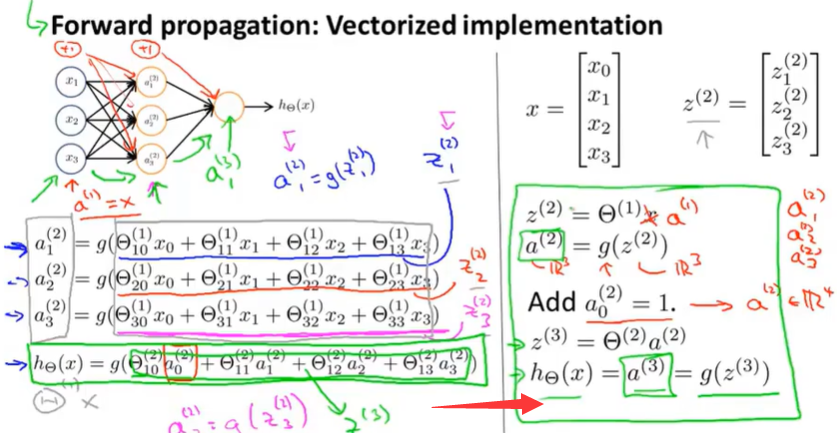
如果你使用右边这些公式,实现它就会得到一个有效的计算h(x)的方法。
(六)神经网络的作用和如何帮助我们学习非线性假设函数
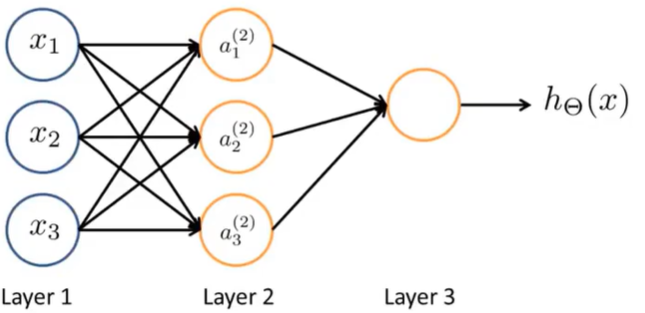
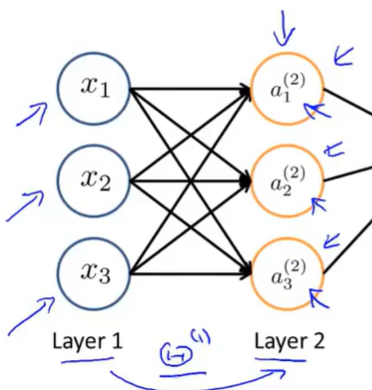
为了更好了了解Neuron Networks的工作原理,我们先把左半部分遮住:
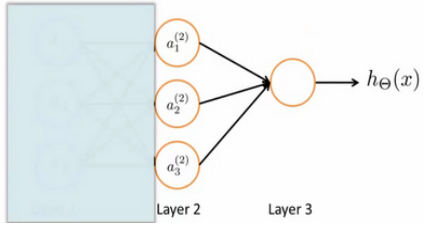
无数的逻辑回归组成了神经网络,神经网络即为立体的logistic回归。

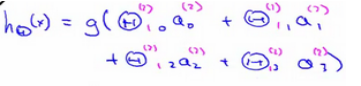
其实神经网络就像是逻辑回归,但是他不是使用原本的x_1,x_2,x_3作为特征,而是使用a_1,a_2,a_3作为新的特征。
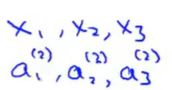
其中a_1,a_2,a_3他们是通过学习得到的函数输入值:具体来说就是从第一层映射到第二层的函数,这个函数由其他参数θ^(1)决定。在神经网络中,它没有用输入特征x1 x2 x3来训练逻辑回归,而是自己训练逻辑回归的输入。
可以想象,如果在θ1中选择不同的参数,有时可以学习到一些很有趣和复杂的特征,就可以得到一个更好的假设
比使用原始输入x1 x2或x3时得到的假设更好,你也可以选择多项式项x1 x2 x3等作为输入项。
但这个算法可以灵活地快速学习任意的特征项。
把这些a1 a2 a3输入这个最后的单元。
实际上它是逻辑回归。
(七)其他神经网络结构

(八)对比逻辑回归和线性回归


我们可以把a_1,a_2,a_3看成更为高级的特征值,也就是x_1,x_2,x_3的进化体,并且它们是由θ与x决定的,因为是梯度下降的,所以a是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将x次方作为特征值更厉害,也能更好的预测新数据。
这就是神经网络相比于逻辑回归和线性回归的优势。
从本质上讲,神经网络能够通过学习得出其自身的一系列特征。
在普通的逻辑回归中,我们被限制为使用数据中的原始特征x_1,x_2,...,x_n,我们虽然可以使用一些二项式项来组合这些特征,但是我们仍然受到这些原始特征的限制。
在神经网络中,原始特征只是输入层,在我们上面三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
三:神经网络是如何计算复杂的非线性函数的输入?(1)---单层神经网络
了解为什么神经网络可以用来学习复杂的非线性假设。
(一)案例一 (异或)---引出and
我们有x_1,x_2两个输入特征(都是二进制的):

在这个例子中,只画出了两个正样本和两个负样本。
但你可以认为这是一个更复杂的机器学习问题的简化版本:

比起后面这种复杂的例子,左边的例子更容易说明问题。
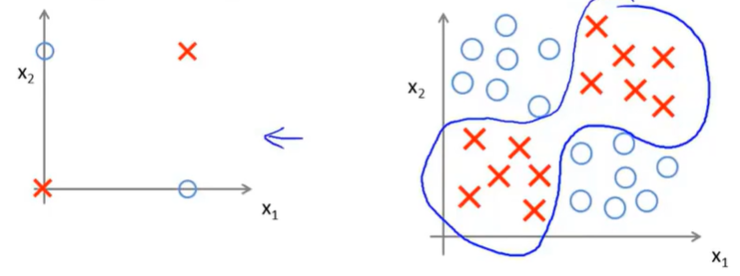
我们可以构建一个神经网络来拟合这样的训练集。

(二)案例二---and运算
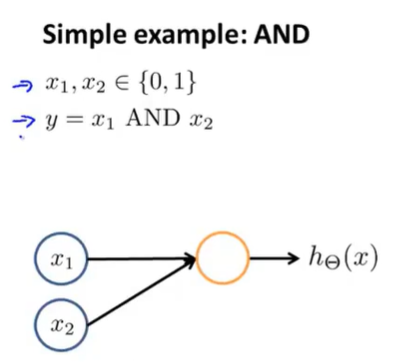
我们怎样得到一个具有单个神经元的神经网络,来计算这个逻辑与函数?
1.我们需要在这里加上一个偏置单元(+1单元)
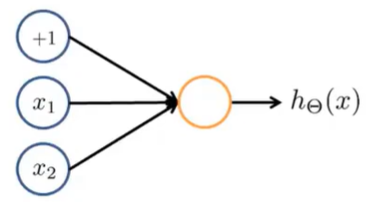
2.需要对神经网络中的权重(参数)进行赋值
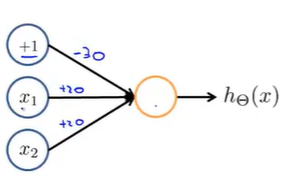
得到假设函数:
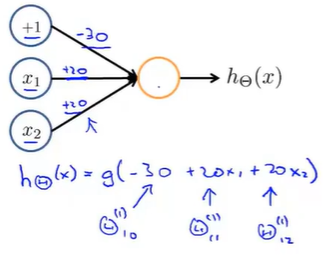
查看sigmoid函数值:
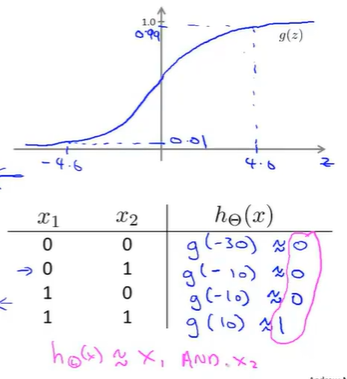
(三)案例三---OR

(三)案例四---NOT

四:神经网络是如何计算复杂的非线性函数的输入?(2)---多层神经网络
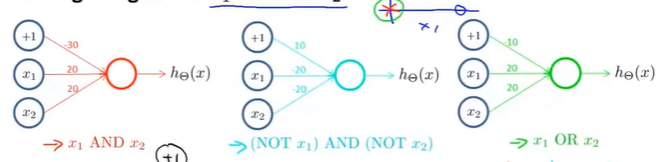
(一)异或
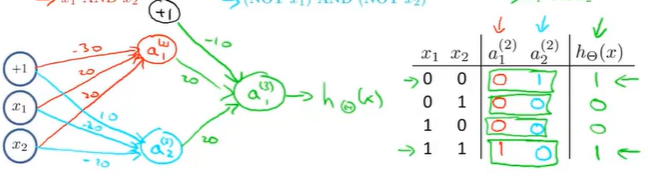
这个神经网络,有一个隐藏层和一个输出层,最后会得到一个非线性的决策边界。用来计算XNOR函数
五:利用神经网络解决多类别分类问题
在神经网络中实现多类别分类,采用的方法本质上是一对多的扩展。
假设有一个计算机视觉的例子,我们不只要识别出图中的汽车,还要识别出行人、摩托车、货车。

我们要做的就是建立一个有四个输出单元的神经网络。
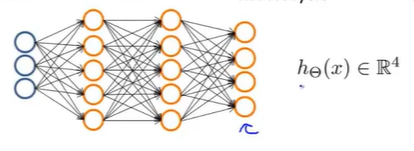
输出变成了一个四维向量。
输入向量x有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现[a b c d]T,且a,b,c,d中仅有一个为1,表示当前类。下面是该神经网络的可能结构示例:
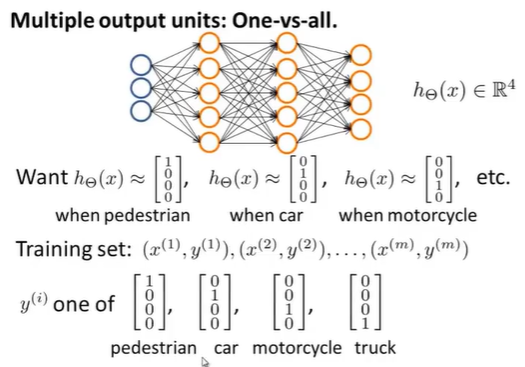
神经网络算法的输出结果为四种可能情形之一:
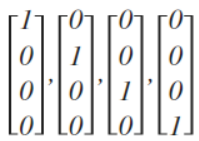
作者:山上有风景
欢迎任何形式的转载,但请务必注明出处。
限于本人水平,如果文章和代码有表述不当之处,还请不吝赐教。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构