题解——[[NOIP2007]树网的核](树的直径)
题解——[NOIP2007]树网的核(加强版)
这道题的原数据太水了,ssw02只讲O(n)做法
题目搬运: BZOJ1999
设T=(V, E, W) 是一个无圈且连通的无向图(也称为无根树),每条边带有正整数的权,我们称T为树网(treenetwork),其中V, E分别表示结点与边的集合,W表示各边长度的集合,并设T有n个结点。 路径:树网中任何两结点a,b都存在唯一的一条简单路径,用d(a,b)表示以a,b为端点的路径的长度,它是该路径上各边长度之和。
我们称d(a,b)为a,b两结点间的距离。 一点v到一条路径P的距离为该点与P上的最近的结点的距离: d(v,P)=min{d(v,u),u为路径P上的结点}。 树网的直径:树网中最长的路径称为树网的直径。对于给定的树网T,直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距ECC(F):树网T中距路径F最远的结点到路径F的距离,即 。 任务:对于给定的树网T=(V, E,W)和非负整数s,求一个路径F,它是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过s(可以等于s),使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核(Core)。必要时,F可以退化为某个结点。
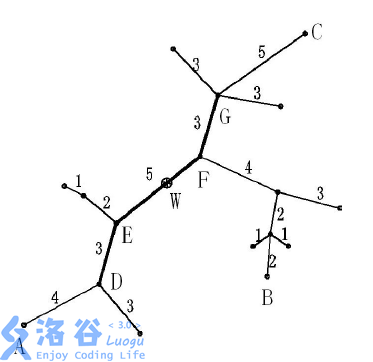
一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。 下面的图给出了树网的一个实例。图中,A-B与A-C是两条直径,长度均为20。点W是树网的中心,EF边的长度为5。如果指定s=11,则树网的核为路径DEFG(也可以取为路径DEF),偏心距为8。如果指定s=0(或s=1、s=2),则树网的核为结点F,偏心距为12。
输入格式
包含n行: 第1行,两个正整数n和s,中间用一个空格隔开。其中n为树网结点的个数,s为树网的核的长度的上界。
设结点编号依次为1, 2, ..., n。 从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“2 4 7”表示连接结点2与4的边的长度为7。
输出格式
输出一个整数表示偏心距。
解题思路
是建立在读者已经会用O(n^2)的贪心算法基础上,实际上也很简单
这道题不用二分,不用多源汇最短路,不用单调队列。
我们实际上只要把树的直径跑出来,再在直径上的每个点(u1,u2,u3,...ut)中跑dfs2(),意义是改点在不经过直径的情况下所能到的最远距离(Lon_dis[])。然后维护一下。
只用扫描和遍历。
具体过程:用同一个指针,在枚举末节点时,移动 tail ,始终保持 末节点和tail节点的距离小于核长度的上界。(因为tail会随末节点的后移而后移)。
AC code:
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN = 100005 ;
inline int read(){
int s = 0 ; char g=getchar() ;
while( g>'9'||g<'0')g=getchar() ;while( g>='0'&&g<='9')s=s*10+g-'0' , g=getchar() ;
return s ;
}
int tot = 1 , head[ MAXN ] , to[ MAXN*2 ] , nex[ MAXN*2 ] , pre[ MAXN ] , w[ MAXN ] ;
int N , M , ans = 0 , dis[ MAXN ] , lon_dis[ MAXN ], p ;//p记录第一次的最远点
int dia[ MAXN ] , sum[ MAXN ] ;
bool v[ MAXN ] ;
int max( int x , int y ){
if( x > y )return x ;return y ;
}
int min( int x , int y ){
if( x > y)return y ; return x ;
}
void add( int x , int y , int z ){
to[ ++tot ] = y , nex[ tot ] = head[ x ] , w[ tot ] = z , head[ x ] = tot ;
}
void dfs( int u , int fa ){//跑直径
pre[ u ] = fa ;
if( ans < dis[ u ] )ans = dis[ u ] , p = u ;
for( register int i = head[ u ] ; i ; i = nex[ i ] ){
if( to[ i ] == fa )continue ;
dis[ to[ i ] ] = dis[ u ] + w[ i ] ;
dfs( to[ i ] , u ) ;
}
}
void dfs2( int u , int fa ){//跑出单点的lon_dis
if( ans < dis[ u ] )ans = dis[ u ] , p = u ;
for( register int i = head[ u ] ; i ; i = nex[ i ] ){
if( to[ i ] == fa || v[ to[ i ] ] )continue ;
dis[ to[ i ] ] = dis[ u ] + w[ i ] ;
dfs( to[ i ] , u ) ;
}
}
int main(){
N = read() , M = read() ; int m1 , m2 , m3 ;
for( register int i = 1 ; i < N ; ++i ){
m1 = read() , m2 = read() , m3 = read() ;
add( m1 , m2 , m3 ) , add( m2 , m1 , m3 ) ;
}
dfs( 1 , 1 ) ; ans = 0 , dis[ p ] = 0 ;
dfs( p , p ) ; v[ p ] = true ;
m1 = p ;
int num = 1 ;
for( register int i = m1 ; i ; i = pre[ i ] , ++num ){
dia[ num ] = i ;
if( pre[ i ] == i )break ;
for( register int k = head[ i ] ; k ; k = nex[ k ] )
if( to[ k ] == pre[ i ] )sum[ num+1 ] = sum[ num ] + w[ k ] ;//sum是直径距离的前缀和,方便查距离
v[ pre[ i ] ] = true ;
}
ans = 0 , dis[ p ] = 0 ;
dfs2( m1 , m1 ) ; lon_dis[ p ] = dis[ p ] ;
for( register int i = m1 ; i ; i = pre[ i ] ){
ans = 0 , dis[ i ] = 0 , p = 0 ;
dfs2( i , i ),lon_dis[ i ] = dis[ p ] ;
if( pre[ i ] == i )break ;
}
int ECC = (1<<30) , tail = 1 ;//指针往后推
for( register int i = 1 ; i <= num ; ++i ){//写得过丑,请屏蔽
int anns = 0 ;
while( sum[ i ] - sum[ tail ] > M && tail <= num )tail++ ;
if( tail > num )break ;
for( register int j = tail ; j <= i ; ++j )anns = max( anns , lon_dis[ j ] ) ;
anns = max( sum[ tail ]-sum[ 1 ] , max( sum[ num ]-sum[ i ] , anns ) ) ;//前缀和之差为两点距离
ECC = min( anns , ECC ) ;
}
printf("%d",ECC) ;
return 0 ;
}
/*
5 2
1 2 5
2 3 2
2 4 4
2 5 3
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号