题解rotinv

rotinv

这是一道让我算错时间复杂度的题 （虽然我对了）
上题：

备注：题目转载自No.7 High School Data Structure Special Training 1

输入输出给出一组：

3
2 2 3

OUT:3

数据范围：

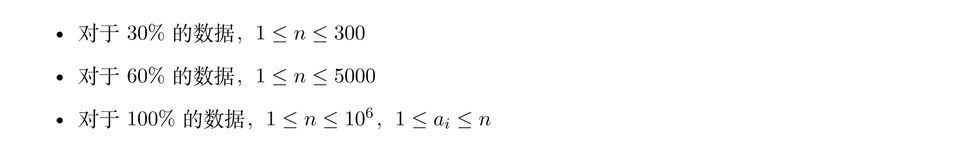
本题的关键，在于如何快速计算出上图中的多个逆序对数。

首先，逆序对常用归并排序和树状数组来进行计算，由于没有修改操作，线段树并不是最优选择，在这里我使用的是树状数组

先将树状数组清零，然后加上以下这段代码即可（倒序求逆序对数）

int  now = m ;//指针（倒序）
  while( now ){
  	tot +=  ask_sum( a[ now ] - 1 ) ;
  	add( a[ now ] , 1 ) ;
  	now-- ;
  }

但是，如果每一组都用其再求一遍逆序对数，复杂度 O( N² log₂N )

直接上天，我们需要更快的方法求出剩下的逆序对数。

详细看，对于每一个 a 值的转移，都可以考虑它在队首和队尾对答案所造成的贡献。而这个贡献，是可以求出的（暴力仍然会TLE），说白了，就是减去在队首的贡献再加上在队尾的贡献

这里给出我的做法 O(N log₂N) 预处理：

for( int  i = 1 ; i <= m ; i++ ){ 
  	b[ i ] = a[ i ] = read() ;num[ a[ i ] ] ++ ;
  }
  for( int  i = 1 ; i <= m ; i++ )if( num[ i ] != 0 )num[ i ]-- ;//去重统计，重复的数会对答案产生影响

void dealb(){
  sort( b + 1 , b + m + 1 , cmp ) ;//复杂度浪费在这里
  int  head = -123456  ;
  b[ m + 1 ] = -654321 ;//边界
  for( int  i = 1 ; i <= m ; ){ //O(N)处理
  	if( b[ i ] != head ){
  		head = b[ i ] ;
  		i++ ;
  		while( b[ i ] == b[ i - 1 ] )i++ ;
  		Yn[ head ] =(ll) m - i + 1 ;//存储贡献
  	}
  }
}

通过预处理，就可以实现在 O（N） 复杂度的递推

总体算法复杂度 O( k1 N log₂N + k2 N ) ，K1，k2为较小常数

AC代码

#include<bits/stdc++.h>
using namespace std;
#define  ll long long 
const  int  MAXN = 1000005 ;
int  m , c[ MAXN ] ,a[ MAXN ] ,b[ MAXN ]   , num[ MAXN ];
//num判重 , Yn记录AC1 中的单个贡献 ， AC 记录单组贡献
ll  tot = 0 , Yn[ MAXN ], AC[ MAXN ];
inline int read()
{
    int s = 0,w = 1;
    char g = getchar();
    while(g<'0'||g>'9'){if(g=='-')w*=-1;g = getchar();}
    while(g>='0'&&g<='9'){s = s*10+g-'0';g = getchar();}
    return s*w;
}
int lowbit( int  x ) 
{
	return x & ( -x ) ;
}
void add( int  x , int  y ) 
{
	for( ; x <= m ; x += x & -x )
	c[ x ] += y ;  
}
int sum( int  x )
{
	int ans = 0 ;
	for( ; x ; x -= x & -x )
	ans += c[ x ] ; 
	return ans ;
}
bool cmp( int  x, int  y ){
	return x > y ;
}
void dealb(){
	sort( b + 1 , b + m + 1 , cmp ) ;
	int  head = -123456  ;
	b[ m + 1 ] = -123666 ;
	for( int  i = 1 ; i <= m ; ){
		if( b[ i ] != head ){
			head = b[ i ] ;
			i++ ;
			while( b[ i ] == b[ i - 1 ] )i++ ;
			Yn[ head ] =(ll) m - i + 1 ;
		}
	}
}

int main()
{
	m = read() ;
	for( int  i = 1 ; i <= m ; i++ ){ 
		b[ i ] = a[ i ] = read() ;num[ a[ i ] ] ++ ;
	}
	for( int  i = 1 ; i <= m ; i++ )if( num[ i ] != 0 )num[ i ]-- ;//去重统计
	dealb() ;
	int  now = m ;//指针
	while( now ){
		tot = AC[ 1 ] = AC[ 1 ] + (ll)sum( a[ now ] - 1 ) ;
		add( a[ now ] , 1 ) ;
		now-- ;
	}
	for( int  i = 1 ; i < m ; i++ ){ 
		AC[ i + 1 ] = AC[ i ] - Yn[ a[ i ] ]*2 + m - 1 - num[ a[ i ] ] ;
		tot += (ll)AC[ i + 1 ] ;
	}
	return  0 ; 
}

总体算法复杂度O( k1 N log₂N + k2 N ) ，K1，k2为较小常数

但HZY大佬又将其优化至O( N log₂N + k N ) ，k为较小常数
方法是 归并排序+类似msort

这里想吐槽一下标程 4.54s 而本文程序 3.24s , HZY大佬 1.54s

最后扔一个随机数据生成器，可以直接使用。

#include<bits/stdc++.h>
using namespace std;
int  m ;
inline int read()
{
    int s = 0,w = 1;
    char g = getchar();
    while(g<'0'||g>'9'){if(g=='-')w*=-1;g = getchar();}
    while(g>='0'&&g<='9'){s = s*10+g-'0';g = getchar();}
    return s*w;
}
int  main()
{
	freopen("rotinv.in","w",stdout);
    m = read() ;
    cout<<2*m<<" ";
    for( int  i = 1 ; i <= m ; i++ ){
    	cout<< abs( ( ( 91*i * i  - i - 8 - 9 ) + 100015 )% m + 1 ) <<" " ; 
        cout<< abs( ( ( 91*i * i  - i - 8 - 9 ) + 100015 )% m + 1 ) <<" " ; 
    }	
	return  0 ;
}

如果你有更好的建议，请在下方留言，非常感谢您的阅读！