# Acwing 291蒙德里安的梦想

Acwing 291蒙德里安的梦想

题意

将\(N*M\)的棋盘分割成若干个\(1*2\)的长方形的方案总数。

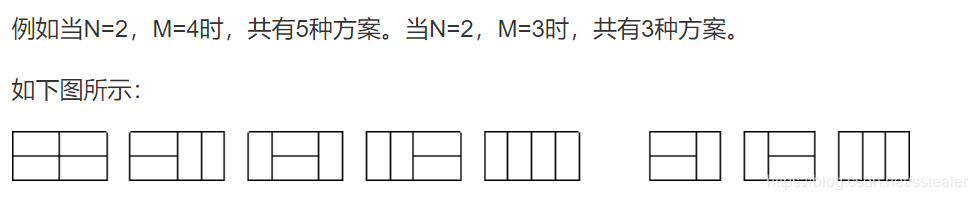
思路

一共有N行，考虑以某一行为分界，将整个棋盘分成两半，第\(i\)行的状态通过第\(i-1\)行转移过来。

由于是分割，（横放的长方形只占一行，不会影响下一行的状态，用于填充该行的空）。所以只需要考虑竖着放的长方形有多少种方法，剩下的空都使用横放的长方形填充（只有一种方案），竖放的长方形的方案数就是答案。

\(f[i][j]\)表示第\(i\)行每一列是否有\(1*2\)长方形的起点，该行每一列的状态通过二进制压缩在j中，就是说\(j\)的二进制的每一位的10表示对应列选还是不选(\(j=(5)_{10}=(101)_2\)表示第一三列有长方形的起点，第二列则没有，该列是否有长方形终点暂时不用管，之后处理会用if判断）。

对于每一行放置完竖放的长方形后，留下来的空，如果有连续的奇数个空连在一起，就无法填充横放的长方形，那么这个竖放长方形的方案就不合理。需要预处理每一行的每一种竖放长方形的方案是否合理。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=12;
int n,m;
bool isok[1<<N];
long long f[N][1<<N];

int main(){
    while (cin>>n>>m,n||m){

        for(int i=0;i<1<<m;i++){//枚举每一列是否有使用，有使用代表该列有出现长方形的起点或者终点
            isok[i]=true;
            int cnt=0;
            for(int j=0;j<m;j++){
                if(i>>j&1){
                    if(cnt&1){isok[i]=false;break;}//连续的奇数个空格,标记该状态不可用
                    cnt=0;
                }
                else cnt++;
            }
            if(cnt&1)isok[i]=false;
        }

        memset(f,0,sizeof f);
        f[0][0]=1;
        for(int i=1;i<=n;i++){//枚举每一行
            for(int j=0;j<1<<m;j++)//枚举该行每一列的状态
                for(int k=0;k<1<<m;k++){//枚举该行上一个状态，也就是上一行的列的使用状态
                    if(j&k || !isok[j|k])continue;//j，k枚举的是列是否出现起点，如果k出现起点，那么下一行k的位置就会出现终点，如果该列又出现起点就会冲突，(j|k)代表了第i行被长方形占据的位置（包括起点和终点）
                    f[i][j]+=f[i-1][k];
                }
        }
        cout<<f[n][0]<<endl;
    }
    return 0;
}