基尔霍夫矩阵

基尔霍夫矩阵

定义：如果图D有总共N个点，那么图D的基尔霍夫矩阵D可以表示为：
1 $ D_{ij} = degree(i) $degree:图的读书
2 $ D_{i,j} = −cnt(i, j)$cnt ：两点之间的边数

性质

引理 : |D| = 0 证：性质：每一行的和 = 0，那么根据行列式恒等变换，全部加到第一列，就是0
引理 : 如果图G不连通，任意余子式\(|M_{ii}| = 0\)
引理：如果图G是一棵树，那么任意余子式\(|M_{ii}| = 1\)。
引理：如果图G是一棵树，那么给矩阵\(|M_{11}|\)加上1之后，余子式\(M_{11} = 1\)。
对于后两条的证明：若我们节点数小n的树都满足
用数学归纳法，递归下去，消掉一个根节点后\(M_{11}\)子树的根节点度数都要+1，最后对角线全部加+1，根据行列式恒等变换就可以拆除一个单位矩阵，和一个值为0的图矩阵

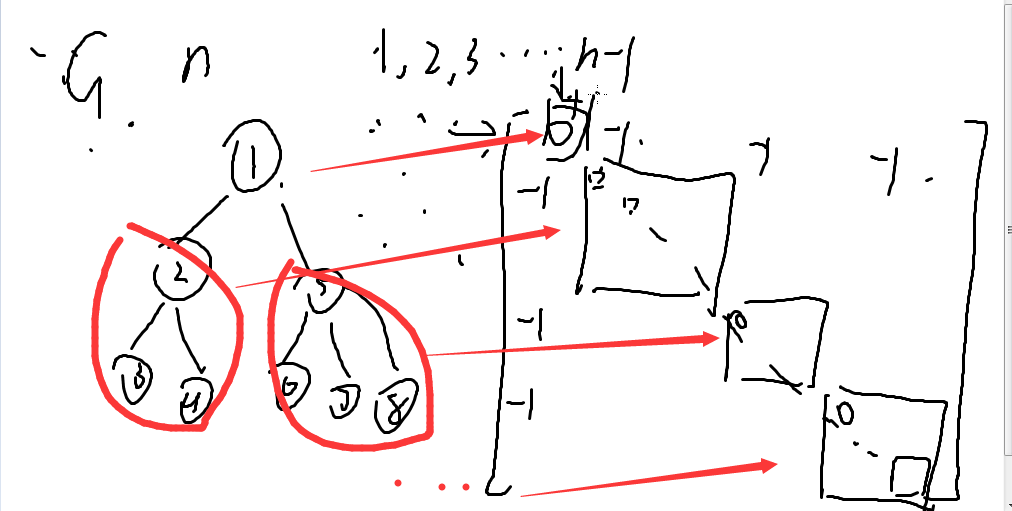
矩阵树定理

一张图的生成树个数就是，任意一主余子式的值
例子：求下面4点完全的生成树个数

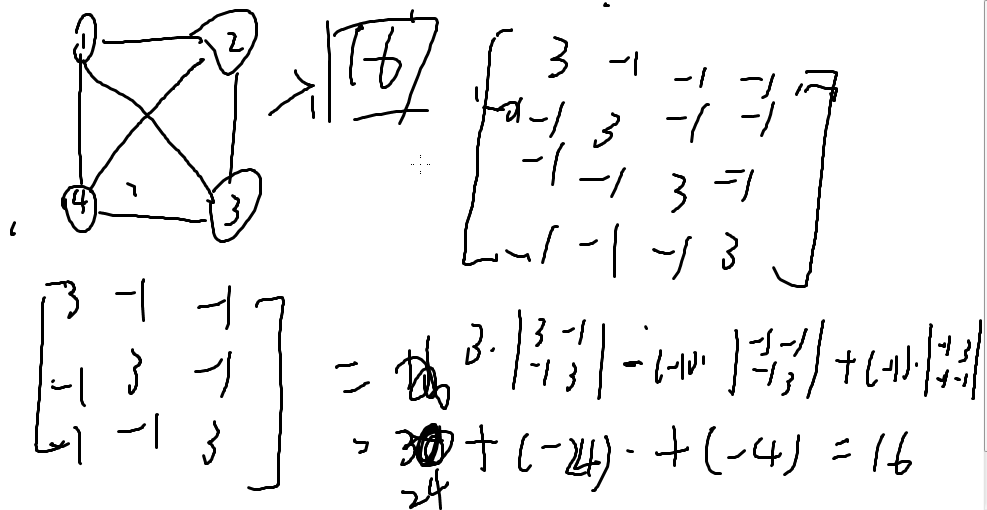
那么得到结论，完全图的生成树个数为点数n的n-2次方
那么问题来了，如何计算行列式的值呢

计算行列式的值

根据性质：行列式的恒等变换
把行列式消成上三角行列式
然后，你就会发现对行列式的值贡献的有且只有对角线的乘积...
复杂度\(O(n^3)\)