切比雪夫距离与曼哈顿距离

曼哈顿距离

很有意思的名字
百度告诉我.........算了你还是自己去百度吧
定义\(a(x1,y1),b(x2,y2)\)，a,b两点的曼哈顿距离就是
\(dis(a,b)=|x1-x2|+|y1-y2|\)

切比雪夫距离

定义\(a(x1,y1),b(x2,y2)\),a,b两点的切比雪夫距离就是
\(dis(a,b)=max(|x1-x2|,|y1-y2|)\)

相互关系

考虑二维笛卡尔坐标系的坐标原点\(O(0,0)\)，
与它的切比雪夫距离为1的点的集合形成的图形是一个边长为2的正方形
与它的曼哈顿距离为1的点的集合形成的图形是一个边长为1的正方形
把这个边长为2的正方形旋转45度再缩小2倍，两个图形即可重合。
考虑求切比雪夫距离的公式：

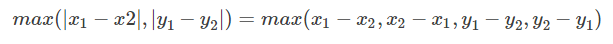
考虑求曼哈顿就离的公式

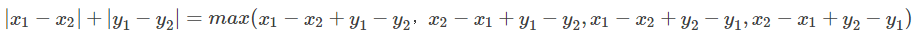
设\(x_{3}=x_{1}+y_1,y_3=x_1−y_1,x_4=x_2+y_2,y_4=x_2−y_2\),待回切比雪夫公式中，就得到了
切比雪夫距离=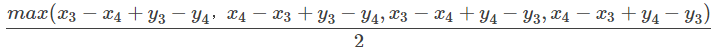
然后切比雪夫距离就可以转化为曼哈顿距离了...
例题：https://www.luogu.org/problemnew/show/P3964