luogu P1941 飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编：

1. 游戏界面是一个长为n ，高为 m 的二维平面，其中有k 个管道（忽略管道的宽度）。

2. 小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

3. 小鸟每个单位时间沿横坐标方向右移的距离为1 ，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度X ，每个单位时间可以点击多次，效果叠加；

如果不点击屏幕，小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时，上升的高度X 和下降的高度Y 可能互不相同。

4. 小鸟高度等于0 或者小鸟碰到管道时，游戏失败。小鸟高度为 m 时，无法再上升。

现在，请你判断是否可以完成游戏。如果可以 ，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入输出格式

输入格式：

 

输入文件名为 bird.in 。

第1 行有3 个整数n ，m ，k ，分别表示游戏界面的长度，高度和水管的数量，每两个

整数之间用一个空格隔开；

接下来的n 行，每行2 个用一个空格隔开的整数X 和Y ，依次表示在横坐标位置0 ~n- 1

上玩家点击屏幕后，小鸟在下一位置上升的高度X ，以及在这个位置上玩家不点击屏幕时，

小鸟在下一位置下降的高度Y 。

接下来k 行，每行3 个整数P ，L ，H ，每两个整数之间用一个空格隔开。每行表示一

个管道，其中P 表示管道的横坐标，L 表示此管道缝隙的下边沿高度为L ，H 表示管道缝隙

上边沿的高度（输入数据保证P 各不相同，但不保证按照大小顺序给出）。

 

输出格式：

 

输出文件名为bird.out 。

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出1 ，否则输出0 。

第二行，包含一个整数，如果第一行为1 ，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

 

输入输出样例

输入样例#1： 复制

10 10 6 
3 9  
9 9  
1 2  
1 3  
1 2  
1 1  
2 1  
2 1  
1 6  
2 2  
1 2 7 
5 1 5 
6 3 5 
7 5 8 
8 7 9 
9 1 3 

输出样例#1： 复制

1
6

输入样例#2： 复制

10 10 4 
1 2  
3 1  
2 2  
1 8  
1 8  
3 2  
2 1  
2 1  
2 2  
1 2  
1 0 2 
6 7 9 
9 1 4 
3 8 10  

输出样例#2： 复制

0
3

说明

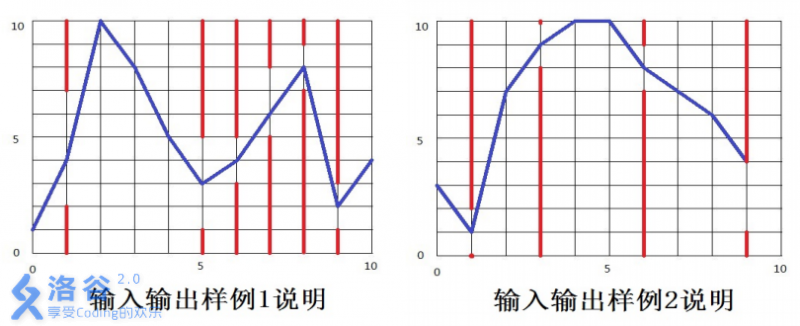
【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

【数据范围】

对于30% 的数据：5 ≤ n ≤ 10，5 ≤ m ≤ 10，k = 0 ，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于50% 的数据：5 ≤ n ≤ 2 0 ，5 ≤ m ≤ 10，保证存在一组最优解使得同一单位时间最多点击屏幕3 次；

对于70% 的数据：5 ≤ n ≤ 1000，5 ≤ m ≤ 1 0 0 ；

对于100%的数据：5 ≤ n ≤ 100 0 0 ，5 ≤ m ≤ 1 0 00，0 ≤ k < n ，0<X < m ，0<Y <m，0<P <n，0 ≤ L < H ≤ m ，L +1< H 。

 

对于dp[i][j]表示第i列时，跳到第j个点的最小花费

这个n*m^2的dp方程很好想，上升的情况枚举上一个点的位置进行转移，转移o (n)，考虑优化，dp[i][j]可以从第i列中上一个转移到的也就是dp[i-up[i-1]]]中选择多跳一次转移而成

复杂度O(1)

注意,转移下降状态要在转移上升状态之后，否则上升状态不满足单调上升，即只进行上下操作其中的一种

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 10007;
const int maxm = 1007;
inline int read() {
    int x=0;
    char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
    return x;
}
int n,m,k;
int up[maxn],down[maxn];
int h[maxn],l[maxn],dp[maxn][maxm];
int in[maxn];
int main() {
    n=read(),m=read(),k=read();
    for(int i=0;i<n;++i) {
        up[i]=read(),down[i]=read();
        h[i]=m+1,l[i]=0;
    }
    h[n]=m+1,l[n]=0;
    for(int p,i=1;i<=k;++i) {
        p=read(),l[p]=read(),h[p]=read();
        in[p]=1;
    }
    std::memset(dp,0x3f,sizeof dp);
    for(int i=1;i<=m;++i)dp[0][i]=0;
    for(int i=1;i<=n;++i) {
        for(int j=min(l[i]+1,l[i-1]+1);j<max(h[i],h[i-1]);++j) {
            if(j>=up[i-1]) {
                dp[i][j]=min(dp[i][j],dp[i-1][j-up[i-1]]+1);
                dp[i][j]=min(dp[i][j],dp[i][j-up[i-1]]+1);//上升
            }
            if(j==m) {
                for(int k=m-up[i-1];k<=m;k++) {
                    dp[i][m]=min(dp[i][m],dp[i-1][k]+1);
                    dp[i][m]=min(dp[i][m],dp[i][k]+1);
                }
            }
            //if(j+down[i-1]<=m)
            //        dp[i][j]=min(dp[i][j],dp[i-1][j+down[i-1]+1]);
        }
        for(int j=l[i]+1;j<h[i];j++){  //下降
            if(j+down[i-1]<=m)
            dp[i][j]=min(dp[i][j],dp[i-1][j+down[i-1]]);    
        }
        for(int j=1;j<=l[i];++j)dp[i][j]=0x3f3f3f3f;
        for(int j=h[i];j<=m;++j)dp[i][j]=0x3f3f3f3f;
        
    }
    int ans=0x3f3f3f3f;
    int cnt=k;
    for(int i=n;i>=1;--i) {
        for(int j=l[i]+1;j<h[i];++j) {
            ans=min(ans,dp[i][j]);
        }
        if(ans!=0x3f3f3f3f)break;
        if(in[i])cnt--;
    }
    if(cnt!=k) {
        puts("0");
        printf("%d\n",cnt);
    }
    else {
        puts("1");
        printf("%d\n",ans);
    }
}