[POI2007]ZAP-Queries
题目描述
Byteasar the Cryptographer works on breaking the code of BSA (Byteotian Security Agency). He has alreadyfound out that whilst deciphering a message he will have to answer multiple queries of the form"for givenintegers  ,
,  and
and  , find the number of integer pairs
, find the number of integer pairs  satisfying the following conditions:
satisfying the following conditions:
 ,
, ,
, , where
, where  is the greatest common divisor of
is the greatest common divisor of  and
and  ".
".
Byteasar would like to automate his work, so he has asked for your help.
TaskWrite a programme which:
reads from the standard input a list of queries, which the Byteasar has to give answer to, calculates answers to the queries, writes the outcome to the standard output.
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。
输入输出格式
输入格式:
The first line of the standard input contains one integer  (
( ),denoting the number of queries.
),denoting the number of queries.
The following  lines contain three integers each:
lines contain three integers each:  ,
,  and
and  (
( ), separated by single spaces.
), separated by single spaces.
Each triplet denotes a single query.
输出格式:
Your programme should write  lines to the standard output. The
lines to the standard output. The  'th line should contain a single integer: theanswer to the
'th line should contain a single integer: theanswer to the  'th query from the standard input.
'th query from the standard input.
输入输出样例
2 4 5 2 6 4 3
2
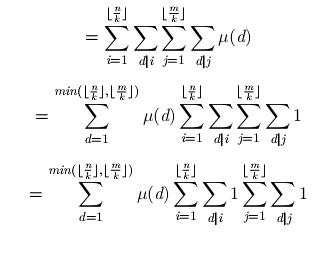
莫比乌斯反演
详见如下
那么就可以在O(n)复杂度内求出
也可以优化到O(sqrt(n))
详见code
#include<cstdio> #include<algorithm> using namespace std; const int maxn = 50010; int a,b,d; int n; int mu[maxn]; int prime[maxn],is_prime[maxn]; void get_mu() { int num=0; mu[1]=1; for(int i=2;i<=50000;i++) { if(!is_prime[i]){ mu[i]=-1;prime[++num]=i; } for(int j=1;j<=num&&i*prime[j]<=50000;j++) { is_prime[i*prime[j]]=1; if(i%prime[j]==0) { mu[i*prime[j]]=0;break; } mu[i*prime[j]]=-mu[i]; } } for(int i=1;i<=50000;i++){ mu[i]=mu[i]+mu[i-1]; } } int main() { scanf("%d",&n); get_mu(); while(n--) { scanf("%d%d%d",&a,&b,&d); a/=d,b/=d; int ans=0;int last; for(int i=1;i<=a&&i<=b;i=last+1) { last=min(a/(a/i),b/(b/i)); ans+=(mu[last]-mu[i-1])*(a/i)*(b/i); } printf("%d\n",ans); } return 0; }

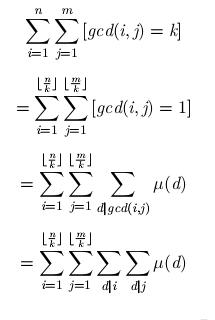
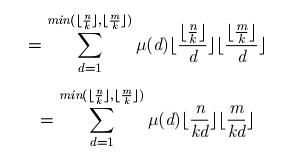

 浙公网安备 33010602011771号
浙公网安备 33010602011771号