网络最大流

 

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

 

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

 

输出格式：

 

一行，包含一个正整数，即为该网络的最大流。

 

输入输出样例

输入样例#1：

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1：

50

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

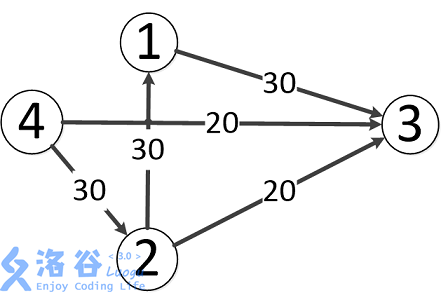
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

dinic算法

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,S,T;
queue<int>que;
const int INF = 0x7fffffff;
const int maxn = 200001; 
inline int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c<='9'&&c>='0'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    return x*f;
  }  
struct node{
    int v,f,next;
}edge[maxn*3];
int num=1,dis[maxn+1];int head[maxn+1];
inline void add_edge(int x,int y,int z)
{
    edge[++num].v=y;edge[num].f=z;edge[num].next=head[x];head[x]=num;
}
bool bfs()
{
    memset(dis,0,sizeof dis);
    que.push(S);
    dis[S]=1;
    while(!que.empty())
    {
        int q=que.front();
        que.pop();
        for(int i=head[q];i;i=edge[i].next){
            if(!dis[edge[i].v]&&edge[i].f)
            {
                dis[edge[i].v]=dis[q]+1;
                que.push(edge[i].v);
            }
        } 
    }
    if(dis[T])return 1;
    return 0;
}
int dfs(int x,int fff)
{
    if(x==T||fff<=0)
        return fff;
    int flow=0,f;
    for(int i=head[x];i;i=edge[i].next)
    {
        if(edge[i].f&&dis[edge[i].v]==dis[x]+1)
        {
            f=dfs(edge[i].v,min(edge[i].f,fff));
            edge[i].f-=f;
            edge[i^1].f+=f;
            flow+=f;
            fff-=f;
            if(fff<=0)break;
        }
    }
    return flow;
}
void dinic()
{
    int ans=0;
    while(bfs())
        ans+=dfs(S,INF);
    printf("%d\n",ans);
}
int  main()
{
    //memset(head,-1,sizeof(head));
    n=read(),m=read();S=read();T=read();
    int a,b,c;
    for(int i=1;i<=m;i++)
    {
        a=read(),b=read(),c=read();
        add_edge(a,b,c);
        add_edge(b,a,0);
    }
    dinic();
    return 0;
}