luogu P1325 雷达安装

题目描述

描述：

假设海岸线是一条无限延伸的直线。它的一侧是陆地，另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上（包括海岸线），并且每个雷达都有相同的扫描范围d。你的任务是建立尽量少的雷达站，使所有小岛都在扫描范围之内。

数据使用笛卡尔坐标系，定义海岸线为x轴。在x轴上方为海洋，下方为陆地。

样例1如图所示

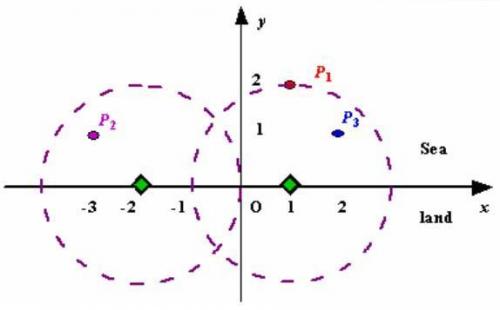
输入输出格式

输入格式：

 

第一行包括2个整数n和d，n是岛屿数目，d是雷达扫描范围。

接下来n行为岛屿坐标。

 

输出格式：

 

一个整数表示最少需要的雷达数目，若不可能覆盖所有岛屿，输出“-1”。

 

输入输出样例

输入样例#1：

3 2
1 2
-3 1
2 1

输出样例#1：

2

 贪心，把问题转化成岛屿覆盖的区域必须有雷达，之后类似于活动安排问题

#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;

#define N 1005
int n,d;
struct island{
    int x;int y;
}is[N];
struct miku{
    double l,r;
    bool operator < (const miku & a)const{
        return r < a.r;
    }
}cd[N];
double calc(double x)
{
    return sqrt(1.0*d*d-x*x);
}
bool vis[N];
int main()
{
    cin>>n>>d;
    for(int i=1;i<=n;i++)
    {
        cin>>is[i].x>>is[i].y;
        if(is[i].y>d||d<0){cout<<"-1"<<endl;return 0;}
    }
    for(int i=1;i<=n;i++)
    {
        double len=calc(is[i].y);
        cd[i].l=is[i].x-len;
        cd[i].r=is[i].x+len;
    }
    sort(cd+1,cd+n+1);
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(!vis[i])
        {
            vis[i]=1;
            for(int j=1;j<=n;j++)
            {
                if(!vis[j] && cd[j].l<=cd[i].r)
                vis[j]=1;
            }
            ans++;
        }
    }
    cout<<ans<<endl;
    return 0;
}