堆

堆

堆和优先队列 Heap and Priority Queue

普通队列：先进先出，后进后出

优先队列：出队顺序和入队顺序无关；和优先级相关

使用数组实现优先队列时间复杂度：O(n^2)，使用堆的时间复杂度：O(nlgn)

最大堆是一颗完全的二叉树，并且任何一个节点都不大于它的父亲节点

所以我们可以使用数组存储二叉堆

二叉树相关概念

构造一个堆，并向里面添加和删除元素

package bobo.algo;

import java.util.*;
import java.lang.*;

// 在堆的有关操作中，需要比较堆中元素的大小，所以Item需要extends Comparable
public class MaxHeap<Item extends Comparable> {

    protected Item[] data;
    protected int count;
    protected int capacity;

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public MaxHeap(int capacity){
        data = (Item[])new Comparable[capacity+1];
        count = 0;
        this.capacity = capacity;
    }

    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    public MaxHeap(Item arr[]){

        int n = arr.length;

        data = (Item[])new Comparable[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )//第一个不是叶子节点的节点
            shiftDown(i);
    }

    // 返回堆中的元素个数
    public int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }

    // 像最大堆中插入一个新的元素 item
    public void insert(Item item){

        assert count + 1 <= capacity;
        data[count+1] = item;
        count ++;
        shiftUp(count);
    }

    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    public Item extractMax(){
        assert count > 0;
        Item ret = data[1];

        swap( 1 , count );
        count --;
        shiftDown(1);

        return ret;
    }

    // 获取最大堆中的堆顶元素
    public Item getMax(){
        assert( count > 0 );
        return data[1];
    }


    // 交换堆中索引为i和j的两个元素
    private void swap(int i, int j){
        Item t = data[i];
        data[i] = data[j];
        data[j] = t;
    }

    //********************
    //* 最大堆核心辅助函数
    //********************
    private void shiftUp(int k){

        while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
            swap(k, k/2);
            k /= 2;
        }
    }

    private void shiftDown(int k){

        while( 2*k <= count ){
            int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
            if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
                j ++;
            // data[j] 是 data[2*k]和data[2*k+1]中的最大值

            if( data[k].compareTo(data[j]) >= 0 ) break;
            swap(k, j);
            k = j;
        }
    }

    // 测试 MaxHeap
    public static void main(String[] args) {

        MaxHeap<Integer> maxHeap = new MaxHeap<Integer>(100);
        int N = 100; // 堆中元素个数
        int M = 100; // 堆中元素取值范围[0, M)
        for( int i = 0 ; i < N ; i ++ )
            maxHeap.insert( new Integer((int)(Math.random() * M)) );

        Integer[] arr = new Integer[N];
        // 将maxheap中的数据逐渐使用extractMax取出来
        // 取出来的顺序应该是按照从大到小的顺序取出来的
        for( int i = 0 ; i < N ; i ++ ){
            arr[i] = maxHeap.extractMax();
            System.out.print(arr[i] + " ");
        }
        System.out.println();

        // 确保arr数组是从大到小排列的
        for( int i = 1 ; i < N ; i ++ )
            assert arr[i-1] >= arr[i];
    }
}

 

 

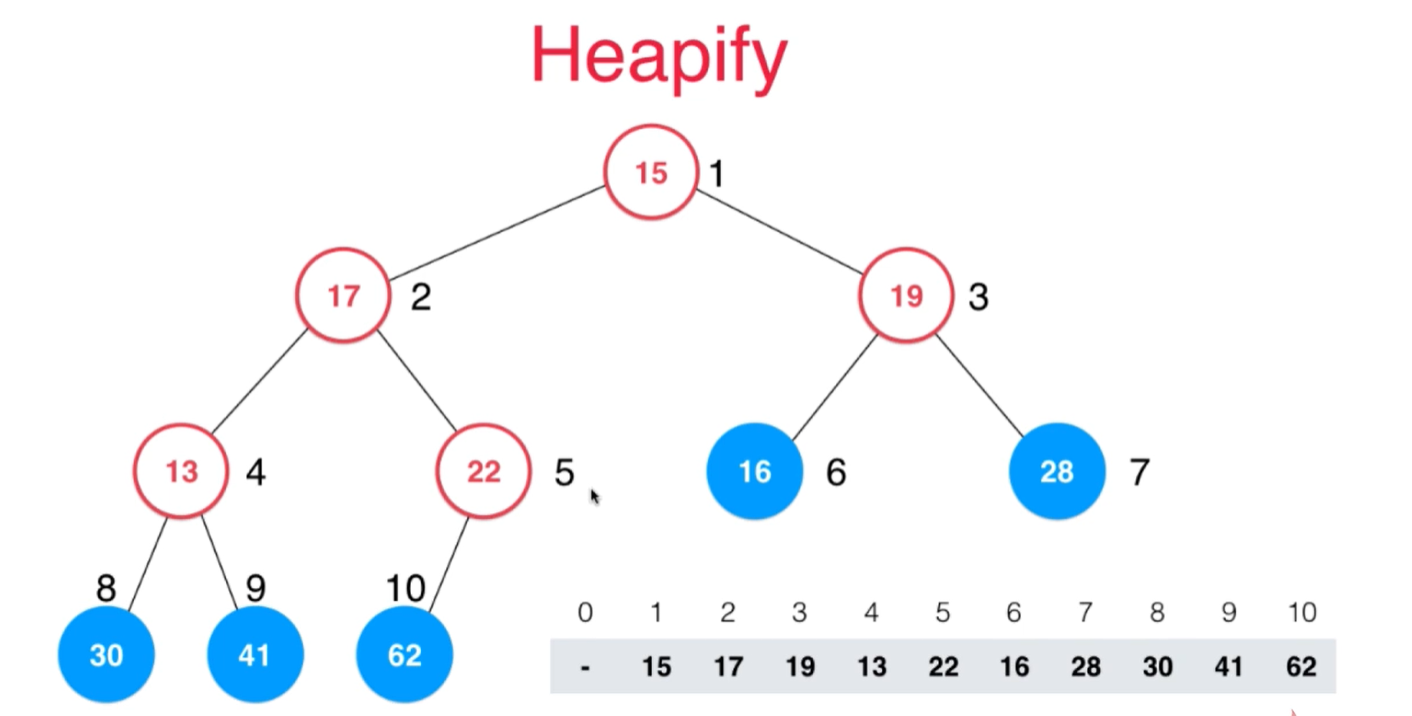
现在的这个完全二叉树还不是一个最大堆，因为并不满足对所有的节点，它的父节点都比自身大这样的一个性质

对一个完全二叉树来说，第一个非叶子节点的索引是这棵完全二叉树的元素个数10除以2得到的那个索引值

如下：从后向前的考察每一个不是叶子节点的这个节点，依次进行shiftDown操作

    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    public MaxHeap(Item arr[]){

        int n = arr.length;

        data = (Item[])new Comparable[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )//第一个不是叶子节点的节点
            shiftDown(i);
    }

索引堆

索引堆：数据和索引这两部分内容分开存储，而真正表示堆的数据时由索引构建成的。

如果没有索引堆，当堆建成之后很难索引到它，初始的时候 系统索引表示是进程id号，当我们把系统任务的数组构建成堆以后，这些数组的索引和系统任务之间就不在产生关联了

比如原理进程id为6的任务优先级提高，组件成堆以后，元素的位置发生改变(可以在元素属性增加一个id号，但是需要把数组遍历一遍才能找到id)。

 

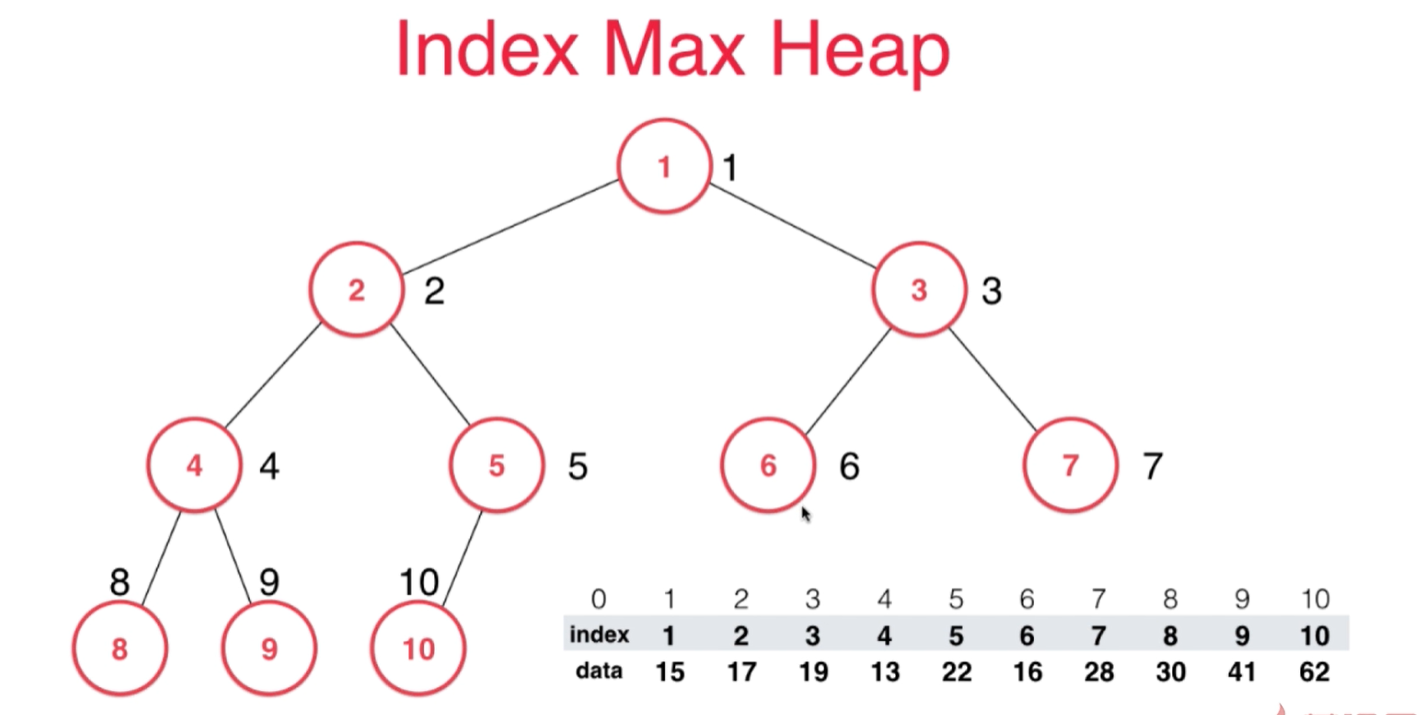
 将上面数组构建成堆以后变成下图所示：

 

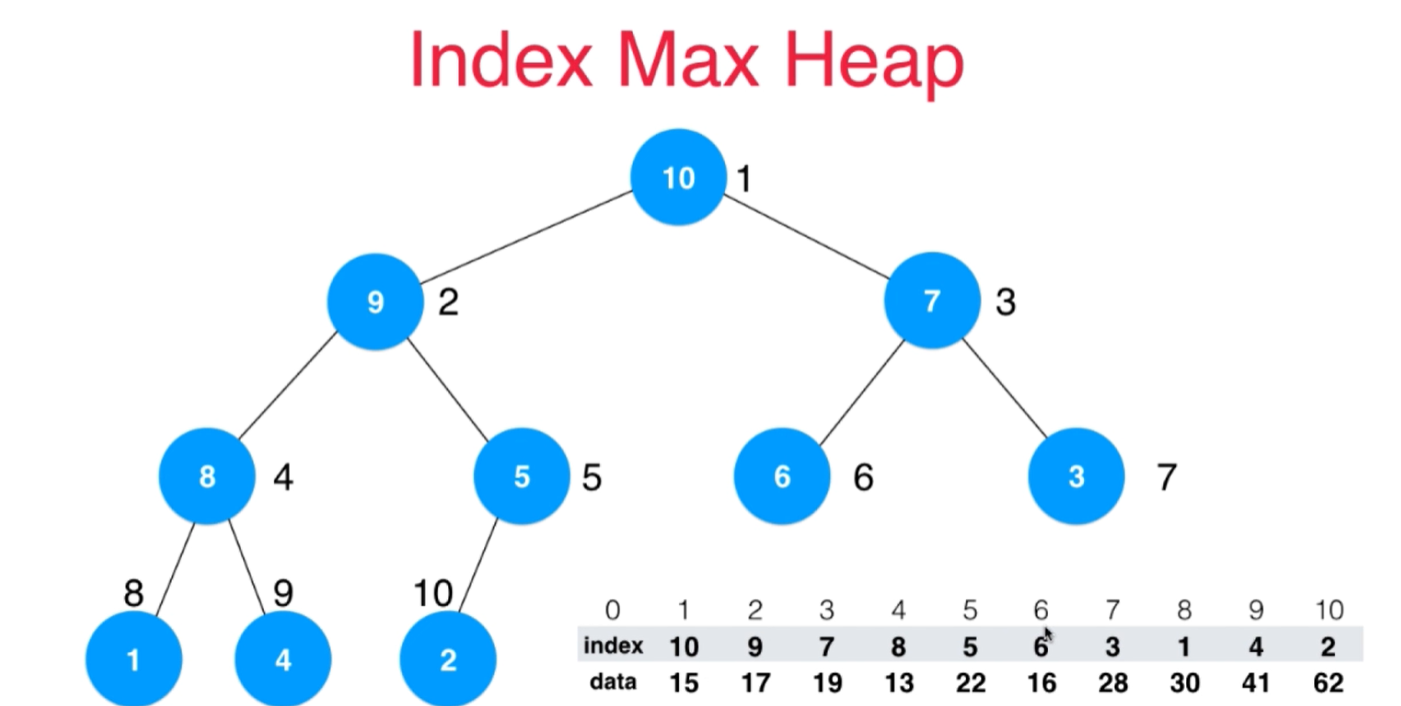
对于data这个域来说它们的内容没有发生任何改变，而真正改变的是index这个域

堆顶的元素index为10表示的就是堆顶的元素是10这个索引锁指向的data也就是62，堆顶元素的左孩子它的索引为9，相应的就是9这个索引所指向的元素41。

索引堆的好处：

1）构建堆的过程只是索引的位置发生交换

2）如果现在想对进程号为7的这个任务优先级提一提，7这个位置的data是28，我们可以提成38，提完之后还要维护堆的性质。维持新的顺序只是根据我们新的data数组来改变index这个数组就好。

在元素比较的时候比较的是data的数据，在元素交换的时候，交换的是索引

package bobo.algo;

import java.util.*;
import java.lang.*;

// 最大索引堆
public class IndexMaxHeap<Item extends Comparable> {

    protected Item[] data;      // 最大索引堆中的数据
    protected int[] indexes;    // 最大索引堆中的索引
    protected int count;
    protected int capacity;

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public IndexMaxHeap(int capacity){
        data = (Item[])new Comparable[capacity+1];
        indexes = new int[capacity+1];
        count = 0;
        this.capacity = capacity;
    }

    // 返回索引堆中的元素个数
    public int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }

    // 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    public void insert(int i, Item item){

        assert count + 1 <= capacity;
        assert i + 1 >= 1 && i + 1 <= capacity;

        i += 1;
        data[i] = item;
        indexes[count+1] = i;
        count ++;

        shiftUp(count);
    }

    // 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
    public Item extractMax(){
        assert count > 0;

        Item ret = data[indexes[1]];
        swapIndexes( 1 , count );
        count --;
        shiftDown(1);

        return ret;
    }

    // 从最大索引堆中取出堆顶元素的索引
    public int extractMaxIndex(){
        assert count > 0;

        int ret = indexes[1] - 1;
        swapIndexes( 1 , count );
        count --;
        shiftDown(1);

        return ret;
    }

    // 获取最大索引堆中的堆顶元素
    public Item getMax(){
        assert count > 0;
        return data[indexes[1]];
    }

    // 获取最大索引堆中的堆顶元素的索引
    public int getMaxIndex(){
        assert count > 0;
        return indexes[1]-1;
    }

    // 获取最大索引堆中索引为i的元素
    public Item getItem( int i ){
        assert i + 1 >= 1 && i + 1 <= capacity;
        return data[i+1];
    }

    // 将最大索引堆中索引为i的元素修改为newItem
    public void change( int i , Item newItem ){

        i += 1;
        data[i] = newItem;

        // 找到indexes[j] = i, j表示data[i]在堆中的位置
        // 之后shiftUp(j), 再shiftDown(j)
        for( int j = 1 ; j <= count ; j ++ )
            if( indexes[j] == i ){
                shiftUp(j);
                shiftDown(j);
                return;
            }
    }

    // 交换索引堆中的索引i和j
    private void swapIndexes(int i, int j){
        int t = indexes[i];
        indexes[i] = indexes[j];
        indexes[j] = t;
    }

    //********************
    //* 最大索引堆核心辅助函数
    //********************

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    private void shiftUp(int k){

        while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){
            swapIndexes(k, k/2);
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    private void shiftDown(int k){

        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[indexes[j+1]].compareTo(data[indexes[j]]) > 0 )
                j ++;

            if( data[indexes[k]].compareTo(data[indexes[j]]) >= 0 )
                break;

            swapIndexes(k, j);
            k = j;
        }
    }

    // 测试索引堆中的索引数组index
    // 注意:这个测试在向堆中插入元素以后, 不进行extract操作有效
    public boolean testIndexes(){

        int[] copyIndexes = new int[count+1];

        for( int i = 0 ; i <= count ; i ++ )
            copyIndexes[i] = indexes[i];

        copyIndexes[0] = 0;
        Arrays.sort(copyIndexes);

        // 在对索引堆中的索引进行排序后, 应该正好是1...count这count个索引
        boolean res = true;
        for( int i = 1 ; i <= count ; i ++ )
            if( copyIndexes[i-1] + 1 != copyIndexes[i] ){
                res = false;
                break;
            }

        if( !res ){
            System.out.println("Error!");
            return false;
        }

        return true;
    }

    // 测试 IndexMaxHeap
    public static void main(String[] args) {

        int N = 1000000;
        IndexMaxHeap<Integer> indexMaxHeap = new IndexMaxHeap<Integer>(N);
        for( int i = 0 ; i < N ; i ++ )
            indexMaxHeap.insert( i , (int)(Math.random()*N) );
        assert indexMaxHeap.testIndexes();
    }
}

索引堆的优化

利用反向查找优化索引堆

 

 

 比如：rev[4]=9表示的是4这个索引在index数组中它的位置是在9这个位置