数据结构——树的相关概念和MySQL索引
平衡二叉树和二叉查找树
至多有两个子节点的树成为二叉树
1)平衡二叉树
1)树的左右高度差不能超过1.
2)任何往下递归的左子树和右子树,必须符合第一条性质
3)没有任何节点的空树或只有跟节点的树也是平衡二叉树
树的节点Node是key value的形式。因为key可能不连续,甚至不是整数,所以我们没办法使用数组来表示,这个时候我们就可以用二叉查找树来实现
2)二叉查找树
树如其名,二叉查找树非常擅长数据查找。
二叉查找树额外增加了如下要求:它的左子树上所有节点的值都小于它,而它的右子树上所有节点的值都大于它。
查找的过程从树的根节点开始,沿着简单的判断向下走,小于节点值的往左边走,大于节点值的往右边走,直到找到目标数据或者到达叶子节点还未找到。
通常设计Node节点来表示key value这样的数据对
二叉查找树的insert

package bobo.algo; // 二分搜索树 // 由于Key需要能够进行比较,所以需要extends Comparable<Key> public class BST<Key extends Comparable<Key>, Value> { // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现 private class Node { private Key key; private Value value; private Node left, right; public Node(Key key, Value value) { this.key = key; this.value = value; left = right = null; } } private Node root; // 根节点 private int count; // 树种的节点个数 // 构造函数, 默认构造一棵空二分搜索树 public BST() { root = null; count = 0; } // 返回二分搜索树的节点个数 public int size() { return count; } // 返回二分搜索树是否为空 public boolean isEmpty() { return count == 0; } // 向二分搜索树中插入一个新的(key, value)数据对 public void insert(Key key, Value value){ root = insert(root, key, value); } //******************** //* 二分搜索树的辅助函数 //******************** // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法 // 返回插入新节点后的二分搜索树的根 private Node insert(Node node, Key key, Value value){ if( node == null ){ count ++; return new Node(key, value); } if( key.compareTo(node.key) == 0 ) node.value = value; else if( key.compareTo(node.key) < 0 ) node.left = insert( node.left , key, value); else // key > node->key node.right = insert( node.right, key, value); return node; } public static void main(String[] args) { } }
二叉查找树的search

package bobo.algo; // 二分搜索树 // 由于Key需要能够进行比较,所以需要extends Comparable<Key> public class BST<Key extends Comparable<Key>, Value> { // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现 private class Node { private Key key; private Value value; private Node left, right; public Node(Key key, Value value) { this.key = key; this.value = value; left = right = null; } } private Node root; // 根节点 private int count; // 树种的节点个数 // 构造函数, 默认构造一棵空二分搜索树 public BST() { root = null; count = 0; } // 返回二分搜索树的节点个数 public int size() { return count; } // 返回二分搜索树是否为空 public boolean isEmpty() { return count == 0; } // 向二分搜索树中插入一个新的(key, value)数据对 public void insert(Key key, Value value){ root = insert(root, key, value); } // 查看二分搜索树中是否存在键key public boolean contain(Key key){ return contain(root, key); } // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null public Value search(Key key){ return search( root , key ); } //******************** //* 二分搜索树的辅助函数 //******************** // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法 // 返回插入新节点后的二分搜索树的根 private Node insert(Node node, Key key, Value value){ if( node == null ){ count ++; return new Node(key, value); } if( key.compareTo(node.key) == 0 ) node.value = value; else if( key.compareTo(node.key) < 0 ) node.left = insert( node.left , key, value); else // key > node->key node.right = insert( node.right, key, value); return node; } // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法 private boolean contain(Node node, Key key){ if( node == null ) return false; if( key.compareTo(node.key) == 0 ) return true; else if( key.compareTo(node.key) < 0 ) return contain( node.left , key ); else // key > node->key return contain( node.right , key ); } // 在以node为根的二分搜索树中查找key所对应的value, 递归算法 // 若value不存在, 则返回NULL private Value search(Node node, Key key){ if( node == null ) return null; if( key.compareTo(node.key) == 0 ) return node.value; else if( key.compareTo(node.key) < 0 ) return search( node.left , key ); else // key > node->key return search( node.right, key ); } // 测试二分搜索树 public static void main(String[] args) { int N = 1000000; // 创建一个数组,包含[0...N)的所有元素 Integer[] arr = new Integer[N]; for(int i = 0 ; i < N ; i ++) arr[i] = new Integer(i); // 打乱数组顺序 for(int i = 0 ; i < N ; i ++){ int pos = (int) (Math.random() * (i+1)); Integer t = arr[pos]; arr[pos] = arr[i]; arr[i] = t; } // 由于我们实现的二分搜索树不是平衡二叉树, // 所以如果按照顺序插入一组数据,我们的二分搜索树会退化成为一个链表 // 平衡二叉树的实现,我们在这个课程中没有涉及, // 有兴趣的同学可以查看资料自学诸如红黑树的实现 // 以后有机会,我会在别的课程里向大家介绍平衡二叉树的实现的:) // 我们测试用的的二分搜索树的键类型为Integer,值类型为String // 键值的对应关系为每个整型对应代表这个整型的字符串 BST<Integer,String> bst = new BST<Integer,String>(); for(int i = 0 ; i < N ; i ++) bst.insert(new Integer(arr[i]), Integer.toString(arr[i])); // 对[0...2*N)的所有整型测试在二分搜索树中查找 // 若i在[0...N)之间,则能查找到整型所对应的字符串 // 若i在[N...2*N)之间,则结果为null for(int i = 0 ; i < 2*N ; i ++){ String res = bst.search(new Integer(i)); if( i < N ) assert res.equals(Integer.toString(i)); else assert res == null; } } }
二叉查找树的遍历
前序遍历:先访问当前节点,再依次递归访问左右子树
中序遍历:先递归访问左子树,再访问自身,再访问右子树
后序遍历:先递归访问左右子树,再访问自身节点

package bobo.algo; // 二分搜索树 // 由于Key需要能够进行比较,所以需要extends Comparable<Key> public class BST<Key extends Comparable<Key>, Value> { // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现 private class Node { private Key key; private Value value; private Node left, right; public Node(Key key, Value value) { this.key = key; this.value = value; left = right = null; } } private Node root; // 根节点 private int count; // 树种的节点个数 // 构造函数, 默认构造一棵空二分搜索树 public BST() { root = null; count = 0; } // 返回二分搜索树的节点个数 public int size() { return count; } // 返回二分搜索树是否为空 public boolean isEmpty() { return count == 0; } // 向二分搜索树中插入一个新的(key, value)数据对 public void insert(Key key, Value value){ root = insert(root, key, value); } // 查看二分搜索树中是否存在键key public boolean contain(Key key){ return contain(root, key); } // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null public Value search(Key key){ return search( root , key ); } // 二分搜索树的前序遍历 public void preOrder(){ preOrder(root); } // 二分搜索树的中序遍历 public void inOrder(){ inOrder(root); } // 二分搜索树的后序遍历 public void postOrder(){ postOrder(root); } //******************** //* 二分搜索树的辅助函数 //******************** // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法 // 返回插入新节点后的二分搜索树的根 private Node insert(Node node, Key key, Value value){ if( node == null ){ count ++; return new Node(key, value); } if( key.compareTo(node.key) == 0 ) node.value = value; else if( key.compareTo(node.key) < 0 ) node.left = insert( node.left , key, value); else // key > node->key node.right = insert( node.right, key, value); return node; } // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法 private boolean contain(Node node, Key key){ if( node == null ) return false; if( key.compareTo(node.key) == 0 ) return true; else if( key.compareTo(node.key) < 0 ) return contain( node.left , key ); else // key > node->key return contain( node.right , key ); } // 在以node为根的二分搜索树中查找key所对应的value, 递归算法 // 若value不存在, 则返回NULL private Value search(Node node, Key key){ if( node == null ) return null; if( key.compareTo(node.key) == 0 ) return node.value; else if( key.compareTo(node.key) < 0 ) return search( node.left , key ); else // key > node->key return search( node.right, key ); } // 对以node为根的二叉搜索树进行前序遍历, 递归算法 private void preOrder(Node node){ if( node != null ){ System.out.println(node.key); preOrder(node.left); preOrder(node.right); } } // 对以node为根的二叉搜索树进行中序遍历, 递归算法 private void inOrder(Node node){ if( node != null ){ inOrder(node.left); System.out.println(node.key); inOrder(node.right); } } // 对以node为根的二叉搜索树进行后序遍历, 递归算法 private void postOrder(Node node){ if( node != null ){ postOrder(node.left); postOrder(node.right); System.out.println(node.key); } } // 测试二分搜索树 public static void main(String[] args) { int N = 1000000; // 创建一个数组,包含[0...N)的所有元素 Integer[] arr = new Integer[N]; for(int i = 0 ; i < N ; i ++) arr[i] = new Integer(i); // 打乱数组顺序 for(int i = 0 ; i < N ; i ++){ int pos = (int) (Math.random() * (i+1)); Integer t = arr[pos]; arr[pos] = arr[i]; arr[i] = t; } // 由于我们实现的二分搜索树不是平衡二叉树, // 所以如果按照顺序插入一组数据,我们的二分搜索树会退化成为一个链表 // 平衡二叉树的实现,我们在这个课程中没有涉及, // 有兴趣的同学可以查看资料自学诸如红黑树的实现 // 以后有机会,我会在别的课程里向大家介绍平衡二叉树的实现的:) // 我们测试用的的二分搜索树的键类型为Integer,值类型为String // 键值的对应关系为每个整型对应代表这个整型的字符串 BST<Integer,String> bst = new BST<Integer,String>(); for(int i = 0 ; i < N ; i ++) bst.insert(new Integer(arr[i]), Integer.toString(arr[i])); // 对[0...2*N)的所有整型测试在二分搜索树中查找 // 若i在[0...N)之间,则能查找到整型所对应的字符串 // 若i在[N...2*N)之间,则结果为null for(int i = 0 ; i < 2*N ; i ++){ String res = bst.search(new Integer(i)); if( i < N ) assert res.equals(Integer.toString(i)); else assert res == null; } } }
二叉查找树的局限性:
如果数据近乎有序:比如1 2 3 4 5 6组成的二叉搜索树退化成了一个链表
解决办法:改造二叉树的实现——>平衡二叉树
AVL树和红黑树
3)AVL树
AVL树是一种平衡二叉查找树 左右子树树高不超过1,增加和删除节点后通过树形旋转重新达到平衡
右旋是以某个节点为中心,将他沉入当前右子节点的位置,而让当前的左子节点作为新树的跟节点
同理,左旋是以某个节点为中心,将它沉入当前左子节点的位置,而让当前右子节点作为新树的根节点
4)红黑树(红黑树本身在树里面是排好顺序的,自身有一些平衡性的操作,所以查找的时候性能比较高)
红黑树和AVL树类似,都是在进行插入和删除元素时,通过特定的旋转来保持自身平衡的,从而获得较高的查找性能。
与AVL树相比红黑树并不追求所有递归子树的高度差不超过1,而是保证从根节点到叶子节点的最长路径不超过最短路径的2倍。
它额外引入了5个约束条件
1)节点只能是红色或黑色
2)根节点必须为黑色
3)所有NIL节点都是黑色的。NIL,即叶子节点下挂的两个虚节点
4)一条路径上不能出现相邻的两个红色节点。
5)在任何递归子树内,根节点到叶子节点的所有路径上包含相同数目的黑色节点。
由于红黑树也是二叉查找树,它们当中每一个节点的比较值都必须大于或等于在它的左子树中的所有节点,并且小于或等于在它的右子树中的所有节点。这确保红黑树运作时能够快速的在树中查找给定的值。
总结一下,即"有红必有黑,红红不相连",上述五个约束条件保证了红黑树的新增、删除、查找的最坏时间复杂度均为O(log n)
5)红黑树与AVL树的比较
https://www.cnblogs.com/ajianbeyourself/p/11173851.html
6)TreeMap
基于红黑树实现的TreeMap提供了平均和最坏复杂度均为O(logn)的增删改查操作,并且实现了NavigableMap接口,该集合最大的特点是key的有序性
7)完全二叉树——>二叉堆
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
B树和B+树
1.B 树可以理解为一个节点可以拥有多于 2 个子节点的多叉查找树,可以减少二叉树的高度
与平衡二叉树相比,B 树利用多个分支(平衡二叉树只有两个分支)节点,而且一个节点可以有两个值,减少获取记录时所经历的节点数。
B 树中同一键值不会出现多次,要么在叶子节点,要么在内节点上。
比如用 1到10这些数字构建一个 B 树结构,其图形如下:
https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html 可用在线网址模拟插入的过程
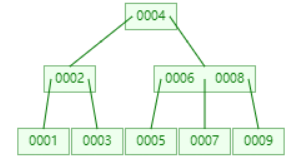
B树的缺点 回旋查找:如果要查大于5的数据,定位到5的时候还要回头查找6。
2.B+ 树是 B 树的变体,定义基本与 B 树一致,与 B 树的不同点:
所有数据都在叶子节点(非叶子节点只存key):这样同样的数据B+树会比B树高度低
各叶子节点用指针进行连接:阻止回旋查询
非叶子节点上只存储 key(索引值) 的信息,这样相对 B 树,可以增加每一页中存储 key 的数量。
B 树是纵向扩展,最终变成一个 “瘦高个”,而 B+ 树是横向扩展的,最终会变成一个 “矮胖子”
还是根据前面提到的这组数字(1到10)举例,它的结构如下:
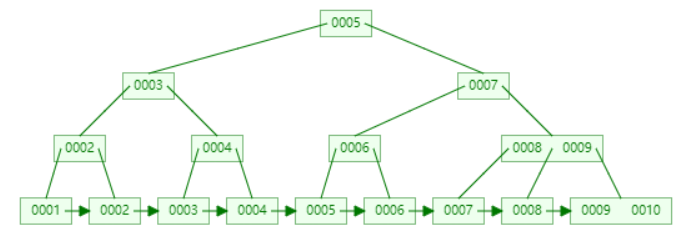
B+树与B树的相同点就是一个节点可以存储两个值
与 B 树的结构最大的区别就是:
它的键一定会出现在叶子节点上,同时也有可能在非叶子节点中重复出现。而 B 树中同一键值不会出现多次。
那么MysqlB+树上可以存储多少数据呢
第一层 16k/(8+6) 16k是节点磁盘大小,8是Long数据类型大小,6是指针 结果= 1170
第二层 16k/(8+6) 16k是节点磁盘大小,8是Long数据类型大小,6是指针 结果= 1170
第三层叶子节点:16k/1k 1k是每条数据的内容(估计) 结果=16
所以一颗B+树大概能放的数据是1170*1170*16=2kw+
注Hash索引和B+索引的区别:
1.哈希索引数据并不是按照索引列的值顺序存储的,故无法用于排序
2.哈希索引只支持等值比较查询,如:=、in()、<=>(安全比较运算符,用来做 NULL 值的关系运算),不支持任何范围查询
3.哈希碰撞
MySQL为什么用自增主键做索引
有面试题会问 为什么不用uuid做索引
1.uuid占用空间大
2.uuid含有字符串 比较大小的速度不如int类型
3.插入一条数据的时候,uuid不是自增,新插入的数据可能在原来的节点之间,为了维持B+树的特征 MySQL会进行一次节点分裂(页分裂)操作 从而浪费时间
innodb和myslam索引区别
InnoDB是聚集索引,使用B+Tree作为索引结构,数据文件是和(主键)索引绑在一起的(data是索引锁住那一行的其他字段的数据)。必须要有主键,通过主键索引效率很高。
MyISAM是非聚集索引,也是使用B+Tree作为索引结构,索引和数据文件是分离的,(data是索引元素对应磁盘文件地址的指针)。
参考文章CSDN:innodb和myslam区别
主键索引:data是索引锁住那一行的其他字段的数据/data是索引元素对应磁盘文件地址的指针
辅助索引:data存的是主键
MySQL中myisam和innodb的主键索引有什么区别?
突然想到一个问题,MySQL不采用Hash索引的原因是因为Hash索引无顺序,为什么不让Hash值有序呢???就像B+树的最后一层一样——>hash值得到的索引是随机的
Mysql索引失效场景的原理
复合索引的B+树一个节点上有两个键值对:
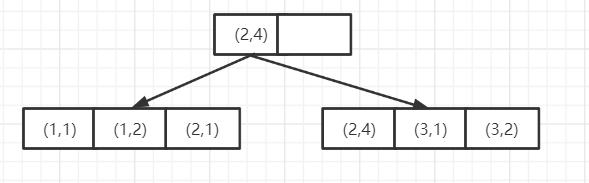
(a,b)比喻两个节点,在a相等的情况下b才有顺序
where a>1 and b=1,在a>1时 查b=1是无序的,这个无序不仅仅体现在叶子节点上面,还体现在非叶子节点上面。
where a like a %1 如果百分号在左边(右缀) 查找以1结尾的数据是无序的(B+树先按照第一个字母去排序,第一个字母相同的时候在按照第二个字母去排序)




