AI笔记 - 数据归一化和标准化

数据归一化和标准化

 

数据标准化/归一化normalization

转自：数据标准化/归一化normalization 

 这里主要讲连续型特征归一化的常用方法。离散参考[数据预处理：独热编码（One-Hot Encoding）]。

基础知识参考：

[均值、方差与协方差矩阵 ]

[矩阵论：向量范数和矩阵范数 ]

数据的标准化（normalization）和归一化

    数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

    目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

归一化的目标

1 把数变为（0，1）之间的小数
        主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速，应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
        归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。 比如，复数阻抗可以归一化书写：Z = R + jωL = R(1 + jωL/R) ，复数部分变成了纯数量了，没有量纲。 
另外，微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

 

归一化后有两个好处

1. 提升模型的收敛速度

如下图，x₁的取值为0-2000，而x₂的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快（理解：也就是步长走多走少方向总是对的，不会走偏）

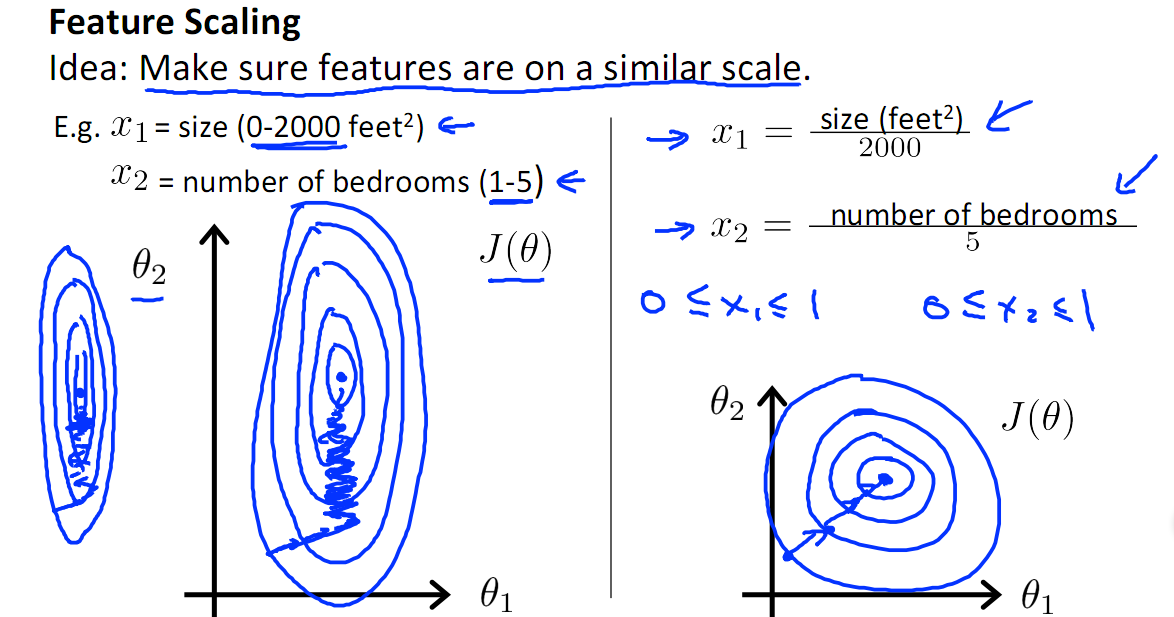
2.提升模型的精度

归一化的另一好处是提高精度，这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，上图中x2的取值范围比较小，涉及到距离计算时其对结果的影响远比x1带来的小，所以这就会造成精度的损失。所以归一化很有必要，他可以让各个特征对结果做出的贡献相同。

    在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。

    在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。

从经验上说，归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。

数据需要归一化的机器学习算法

需要归一化的模型：

        有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM（距离分界面远的也拉近了，支持向量变多？）。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。
        有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression（因为θ的大小本来就自学习出不同的feature的重要性吧？）。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

不需要归一化的模型：

        ICA好像不需要归一化（因为独立成分如果归一化了就不独立了？）。

       基于平方损失的最小二乘法OLS不需要归一化。

[线性回归与特征归一化(feature scaling)]

皮皮blog

 

 

常见的数据归一化方法

min-max标准化(Min-max normalization)/0-1标准化(0-1 normalization)

也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下：

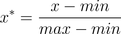
其中max为样本数据的最大值，min为样本数据的最小值。

def Normalization(x):
    return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]

如果想要将数据映射到[-1,1]，则将公式换成：

 

 

x∗=x−xmeanxmax−xmin

 

x_mean表示数据的均值。

def Normalization2(x):
    return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]

这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

log函数转换

通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

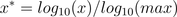
看了下网上很多介绍都是x*=log10(x)，其实是有问题的，这个结果并非一定落到[0,1]区间上，应该还要除以log10(max)，max为样本数据最大值，并且所有的数据都要大于等于1。

atan函数转换

用反正切函数也可以实现数据的归一化。

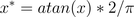
使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上，而并非所有数据标准化的结果都映射到[0,1]区间上。

z-score 标准化(zero-mean normalization)

最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法，spss默认的标准化方法就是z-score标准化。

也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。

经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：

 

 

x∗=x−μσ

其中μ为所有样本数据的均值，σ为所有样本数据的标准差。

z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。

标准化的公式很简单，步骤如下

　　1.求出各变量（指标）的算术平均值（数学期望）xi和标准差si ；
　　2.进行标准化处理：
　　zij=（xij－xi）/si
　　其中：zij为标准化后的变量值；xij为实际变量值。
　　3.将逆指标前的正负号对调。
　　标准化后的变量值围绕0上下波动，大于0说明高于平均水平，小于0说明低于平均水平。

def z_score(x, axis):
    x = np.array(x).astype(float)
    xr = np.rollaxis(x, axis=axis)
    xr -= np.mean(x, axis=axis)
    xr /= np.std(x, axis=axis)
    # print(x)
    return x

为什么z-score 标准化后的数据标准差为1?

x-μ只改变均值，标准差不变，所以均值变为0

(x-μ)/σ只会使标准差除以σ倍，所以标准差变为1

皮皮blog

Decimal scaling小数定标标准化

这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性A的取值中的最大绝对值。

将属性A的原始值x使用decimal scaling标准化到x'的计算方法是：
x'=x/(10^j)
其中，j是满足条件的最小整数。
例如 假定A的值由-986到917，A的最大绝对值为986，为使用小数定标标准化，我们用每个值除以1000（即，j=3），这样，-986被规范化为-0.986。
注意，标准化会对原始数据做出改变，因此需要保存所使用的标准化方法的参数，以便对后续的数据进行统一的标准化。

Logistic/Softmax变换

logistic函数和标准正态函数

新数据=1/（1+e^(-原数据)）

 

P(i)=11+exp(−θTix)

 

这个函数的作用就是使得P(i)在负无穷到0的区间趋向于0，在0到正无穷的区间趋向于1。同样，函数（包括下面的softmax）加入了e的幂函数正是为了两极化：正样本的结果将趋近于1，而负样本的结果趋近于0。这样为多类别分类提供了方便（可以把P(i)看作是样本属于类别i的概率）。

 

logit(P) = log(P / (1-P)) = a + b*x 以及 probit(P) = a + b*x

这两个连接函数的性质使得P的取值被放大到整个实数轴上。

事实上可以把上面的公式改写一下：

P = exp(a + b*x) / (1 + exp(a + b*x)) 或者 P = pnorm(a + b*x)（这个是标准正态分布的分布函数）

 

 

 

Note: 上半部分图形显示了概率P随着自变量变化而变化的情况，下半部分图形显示了这种变化的速度的变化。可以看得出来，概率P与自变量仍然存在或多或少的线性关系，主要是在头尾两端被连接函数扭曲了，从而实现了[0,1]限制。同时，自变量取值靠近中间的时候，概率P变化比较快，自变量取值靠近两端的时候，概率P基本不再变化。这就跟我们的直观理解相符合了，似乎是某种边际效用递减的特点。

[logistic回归的一些直观理解(1.连接函数 logit probit)]

Softmax函数

是logistic函数的一种泛化，Softmax是一种形如下式的函数：

 

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的Softmax值就是

也就是说，是该元素的指数，与所有元素指数和的比值

为什么要取指数，第一个原因是要模拟 max 的行为，所以要让大的更大。第二个原因是需要一个可导的函数。

 

通过softmax函数，可以使得P(i)的范围在[0,1]之间。在回归和分类问题中，通常θ是待求参数，通过寻找使得P(i)最大的θi作为最佳参数。

此外Softmax函数同样可用于非线性估计，此时参数θ可根据现实意义使用其他列向量替代。

Softmax函数得到的是一个[0,1]之间的值，且∑Kk=1P(i)=1，这个softmax求出的概率就是真正的概率，换句话说，这个概率等于期望。

[Softmax 函数及其作用（含推导） ]

[Machine Learning - VI. Logistic Regression逻辑回归 (Week 3) ]

 

模糊量化模式

 

新数据=1/2+1/2sin[派3.1415/（极大值-极小值）*（X-（极大值-极小值）/2） ] X为原数据