浅谈质数与同余

浅谈质数与同余

---

一、质数

定义：除了1和本身两个数都不能被整除的自然数叫做质数，否则为合数。
0和1既不是质数也不是合数，最小的合数是4，
最小的质数是2，是唯一的偶质数，质数有无穷多个
质数分布定理：
对正实数x，定义P(x)为不大于x的质数个数，则有P(x)=O(x/lnx)
由质数定理可以给出第n个质数p(n)的渐进估计：p(n)≈nlnn

二、唯一分解定理（算术基本定理）

任意大于1的自然数都能被质数的质数幂的乘积表示
运用：试除法（质因数分解或求一个数的约数）、质数判定
时间复杂度O(sqrt(n))
由此衍生出埃式筛法和线性筛法（欧拉筛法）
埃式筛法时间复杂度为O(nloglogn)
线性筛法时间复杂度为O(n)

埃式筛法

先将2的倍数删去，再将3的倍数删去，即按顺序将质数的倍数删去

for (int i=2;i<=n;i++)
if (!v[i]){
    prime[+cnt]=i;
    for (int j=i+i;j<=n;j+=i) v[j]=1;
}

线性筛法

让每个合数只被最小的素因子筛除,这样每个数最多只被筛一次。
这个性质被广泛运用于数论函数的求解
洛谷P3383 【模板】线性筛素数

整除

若d能被a整除，记作d|a，即d是a约数，a是d的倍数
若d|a，则d|ka；
若a|b且b|a，则a=b；
若a|b且b|c，则a|c;
若a|b且c|d，则ac|bd；
若c|a且c|b，则c|(ma+nb)

唯一分解定理（算术分解定理）的推论

若可以将n分解为p1 ^ c1p2 ^ c2...pk ^ ck(n>1)
则n的正约数个数为(c1+1)(c2+1)...(ck+1)
n的所有正约数的和为(1+p1+p1 ^ 2+...+p1^ c1)...(1+pk+pk^ 2+...+pk^ck)
由乘法原理得到，下式可以用等比数列求和实现

运用

如果一种转移关系j->i且j是i的约数，那么有两种方法
约数法：O(n sqrt(n))先枚举i再枚举约数j。
一个数约数个数上限为2sqrt n
倍数法：O(nlogn)先枚举j再枚举倍数i。
n个数的倍数个数为n/1+n/2+...+n/n≈nlogn
显然倍数法时间复杂度更优
有的情况可以用埃式筛法，当然倍数法会更加广泛

三、最大公约数与最小公倍数

若d|a,d|b，则d是a和b的公约数，在所有的d中最大的一个称为a和b的最大公约数
若a|m,b|m，则m是a和b的公倍数，在所有的m中最小的一个称为a和b的最小公倍数
性质：
(1)a和b的所有公约数是gcd(a,b)的约数，所有公倍数是lcm(a,b)的倍数
(2)lcm(ma,mb)=mlcm(a,b),gcd(ma,mb)=mgcd(a,b)
(3)gcd(a,0)=a,gcd(a,b)lcm(a,b)=ab，用于求gcd和lcm

四、求两个数的最大公约数

（1）分解质因数：得到的指数 取小的一方
（2）更相减损法：gcd(a,b)=gcd(a,b-a)
证明：若d|a,d|(b-a)，则d|b，反之亦然
（3）欧几里得算法：gcd(a,b)=gcd(b,a mod b),b≠0
（4）大整数求最大公约数：
若a,b为偶数，gcd(a,b)=2*gcd(a/2,b/2)
若a为偶数，b为奇数，gcd(a,b)=gcd(a/2,b)
若a为奇数，b为偶数，gcd(a,b)=gcd(a,b/2)
若a,b为奇数，gcd(a,b)=gcd(a,b-a)

五、欧拉函数

若gcd(a,b)=1，则a和b互质
在自然数1到n中与n互质的个数称为欧拉函数，记作φ(n)
根据容斥定理可以得到φ(n)=n∏(p-1)/p
由于φ是积性函数，所以φ(ab)=φ(a)φ(b)(gcd(a,b)=1)
∑[d|n]φ(d)=n，∑[gcd(n,i)==1]i=n*φ(n)/2
根据以上性质，可以用各种筛法解决

六、同余

定义1：给定正整数m，若用m除两个整数a和b所得余数相同，称a和b对模m同余，记作a≡b(mod m)，并称该式子为同余式；否则称a和b对模m不同余
定义2：整数的集合被分为m个不同的集合，这些集合被称为模m剩余类（同余类）。每个同余类的任意两个整数都是模m同余的。
定理1：
a≡b(mod m)，当且仅当m|(a-b)
定理2：
a≡b(mod m)，当且仅当存在整数k，使得a=b+km

性质

对于整数a,b,c和自然数m,n，对模m同余满足：
1、自反性：a≡a(mod m)
2、对称性：若a ≡ b(mod m)，则b ≡ a(mod m)
3、传递性：若a ≡ b(mod m)，b ≡ c(mod m)，则a ≡ c(mod m)
4、同加性：若a ≡ b(mod m)，则a+c ≡ b+c(mod m)
5、同乘性：若a ≡ b(mod m)，则ac ≡ bc(mod m)
6、同幂性：若a ≡ b(mod m)，则a^n ≡ b^n(mod m)
7、若a mod p=x,a mod q=x，其中p,q互质，则a mod (pq)=x
注意，同余不满足同除性，即不满足a/n ≡ b/n(mod m)

七、欧拉定理和费马小定理

欧拉定理：a^φ (4) ≡1(mod p)(gcd(a,p)=1)
费马小定理：a^(p-1)≡1(mod p)(gcd(a,p)=1)
扩展欧拉定理：

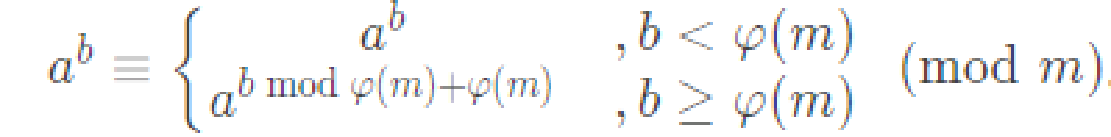
洛谷P4139 上帝与集合的正确用法
求2⁽²(2^...)) mod p，直接套用上式递归即可

八、裴蜀定理与欧几里得算法

ax+by=c存在整数解当且仅当gcd(a,b)|c
扩展欧几里得算法实现求解二元一次不定方程的整数解
若求出ax'+by'=gcd(a,b)，那么将等式两边变为原来的c/gcd(a,b)倍
设x0,y0是ax+by=gcd(a,b)的一个特解，那么通解为
x=x0+b/gcd(a,b)t,
y=y0-a/gcd(a,b)t,
t为任意整数，可以应用至求最小非负整数解

九、乘法逆元

定义：若整数b,m互质，并且b|a，则存在一个整数x，
使得a/b≡ax(mod m)。称x为b的模m乘法逆元，记为b^-1(mod m)。
因为a/b≡ax ≡a/bbb-1(mod m)，所以bb-1 ≡1(mod m)
所以，求b的逆元，等价于求同余方程bx ≡1(mod m)的解。
可以通过扩展欧几里得算法实现
若m是质数可以通过费马小定理实现
当i<p时，有递推式inv[i]=(p-p/i)*inv[p mod i] mod p

十、中国剩余定理（CRT）

十一、扩展中国剩余定理（ExCRT）

用扩展欧几里得算法合并两个方程组
数学归纳法：假设求出了前k-1个方程构成的方程组的一个解x，记m=lcm(m1,m2,…,mk-1)， 则x+im(i为任意整数)是前k-1个方程的解。
考虑第k个方程，求出一个整数t，使得x+tm≡ak(mod mk)，该方程等价于tm ≡ak-x(mod mk)，
其中t是未知量，可以用扩展欧几里得判断该方程是否有解。如果有解，求出t值，则前k个方程构成的方程组的一个解为x’=x+tm。
特别的，第一个方程的解x=a1

---

本人csdn博客

谢谢阅读