Manacher

在O(n)的求出以某个位置为对称中心的回文串长度最长是多少

具体操作

先将字符串的每个字符之间加上\(\#\)，左右边界再加两个不同的字符，如\(abcd->|\#a\#b\#c\#d\#/\)

这样就使每个回文串都有一个回文中心了

然后定义mx,p，mx为已有回文串覆盖到的最右边界，p为其回文中心

对于枚举到的回文中心i，分三类讨论

1.如果回文串右端没有超过mx，那么因为在以p为回文中心的回文串中，所以其回文长度就是对应点j的回文长度（关于p对称）

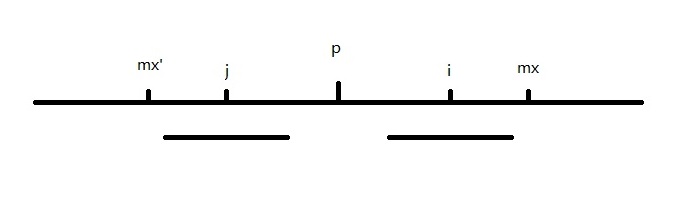
2.回文串右端超过mx了，那么先把回文串内的部分存过来，然后再尝试增大回文长度（即匹配左右端点）

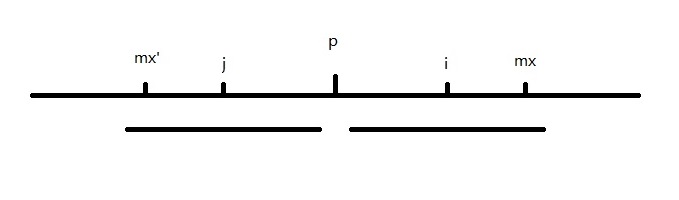
3.回文中心在mx以外，那么初始回文长度为1，然后增大回文长度

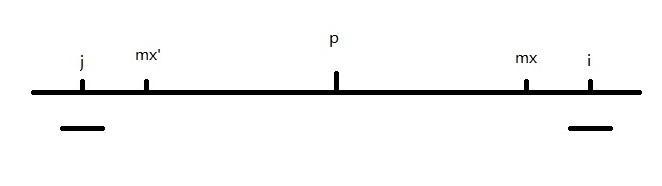
以上三种操作，可以解决所有情况的回文串，那么考虑下时间：

每次从对应点存过来都是O(1)的，那么n个点就是O(n)

对于增大回文长度，每次匹配都会使mx增大，而\(mx\leqslant n\)，所以时间是O(n)的

综上所述，Manacher的时间复杂度是O(n)的

模板

Manacher(luogu 3805)

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 110000010
using namespace std;
int n, ans, l[N*2], s[N*2];
string str;
void Manacher()
{
	int mid = 0, mx = 0;
	for (int i = 1; i <= n; ++i)
	{
		if (i < mx) l[i] = min(l[mid * 2 - i], mx - i);
		else l[i] = 1;
		while(s[i + l[i]] == s[i - l[i]]) l[i]++;
		if (i + l[i] > mx)
		{
			mid = i;
			mx = i + l[i];
		}
		ans = max(ans, l[i]);//回文长度乘2和#的除2抵消了
	}
	return;
}
int main()
{
	cin>>str;
	n = str.size();
	s[0] = s[1] = '#';//这里是用‘#’和0作边界符号
	for (int i = 1; i <= n; ++i)
	{
		s[i * 2] = str[i - 1];
		s[i * 2 + 1] = '#';
	}
	n = n * 2 + 2;
	s[n] = 0;
	Manacher();
	printf("%d", ans - 1);
	return 0;
}