Link-Cut Tree(LCT)
前言
感谢\(Quant\ Ask\)大爷帮助
Link-Cut Tree
在LCT中,对于一棵树,用到了实链剖分,就是按虚实边对其进行剖分
树上的虚实边是可以动态变化,所以在LCT中用到了伸展树(Splay)来维护由若干实边连接成的实链(深度单调递增)
在Splay中x的左子节点连接的是深度比x小的点,右子节点连接的是深度比x大的点
各种操作
access
access(x)是使x到根节点路径上的边全部化为实边,也就是提取x到根节点的实链
例子
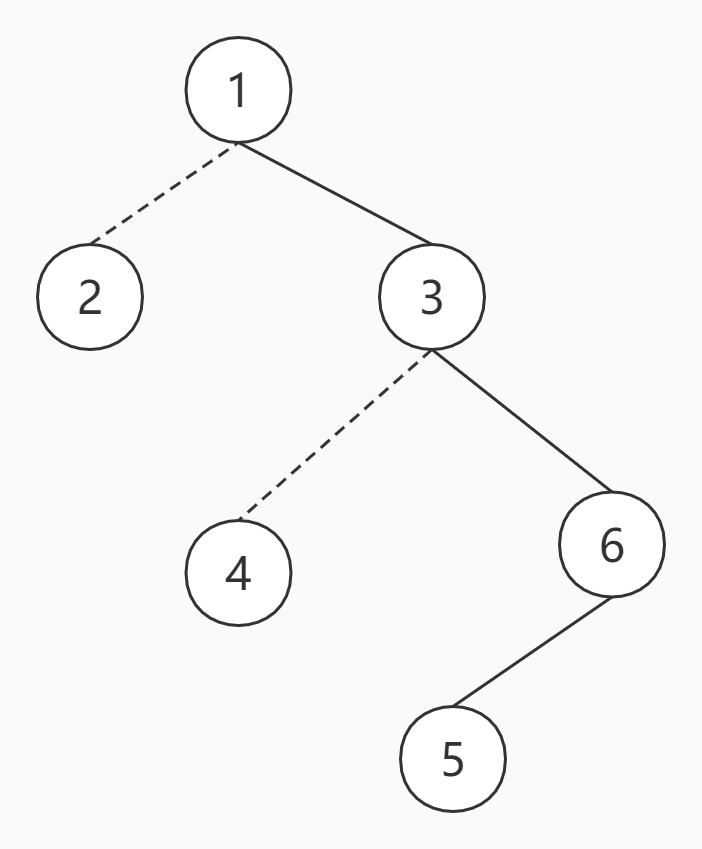
对于一棵树,其虚实边连接如下
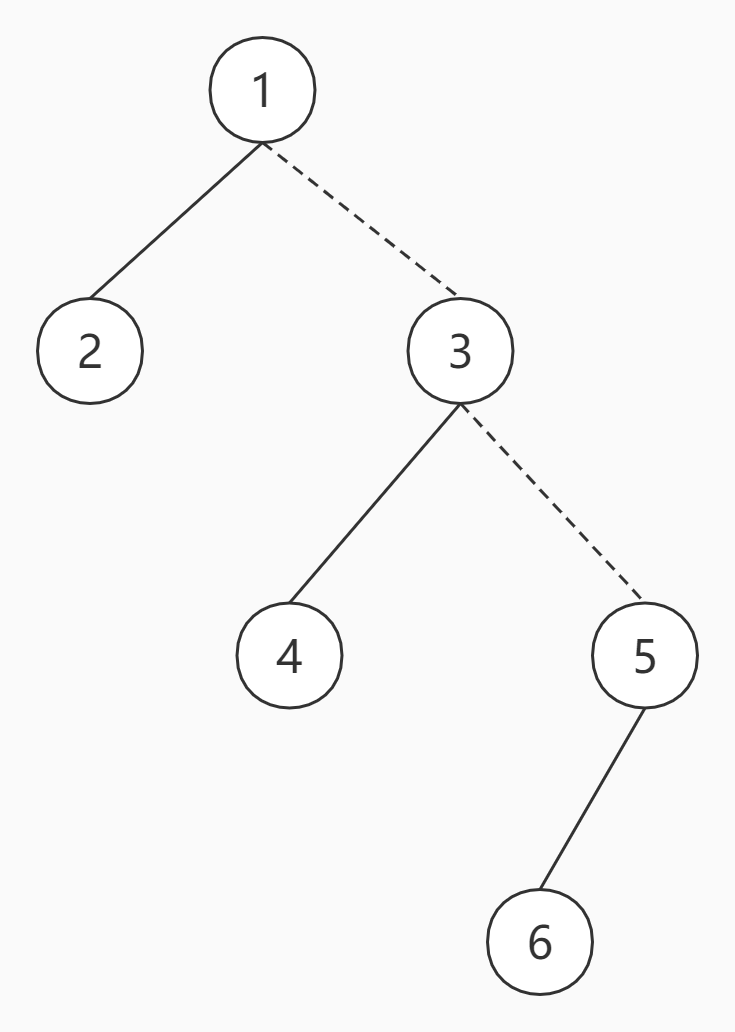
那么它所建成的LCT可能是下面的树(虚边是原树中的连边,实边为Splay中的连边)
此时进行access(6),过程如下
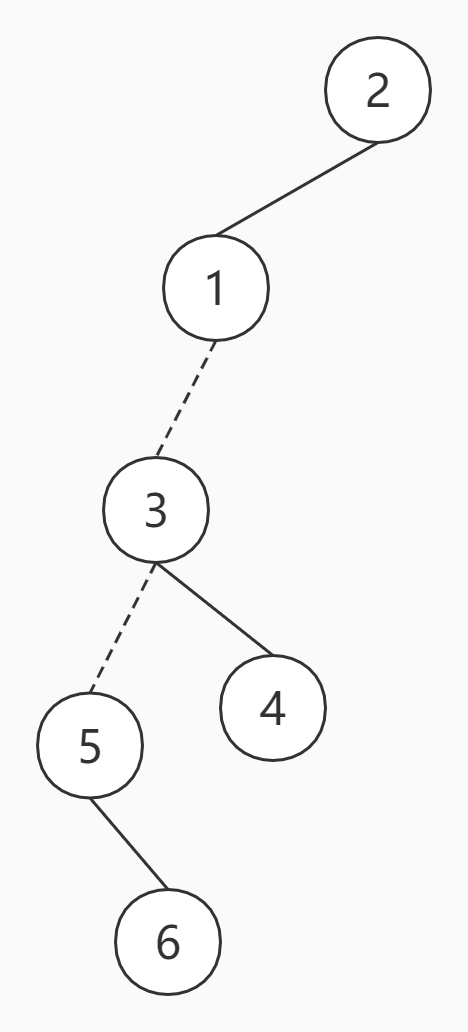
把6旋转到Splay的根节点
因为右子节点深度比6大,所以切断左子节点(这里6没有右子节点),即把6的右子节点设为0
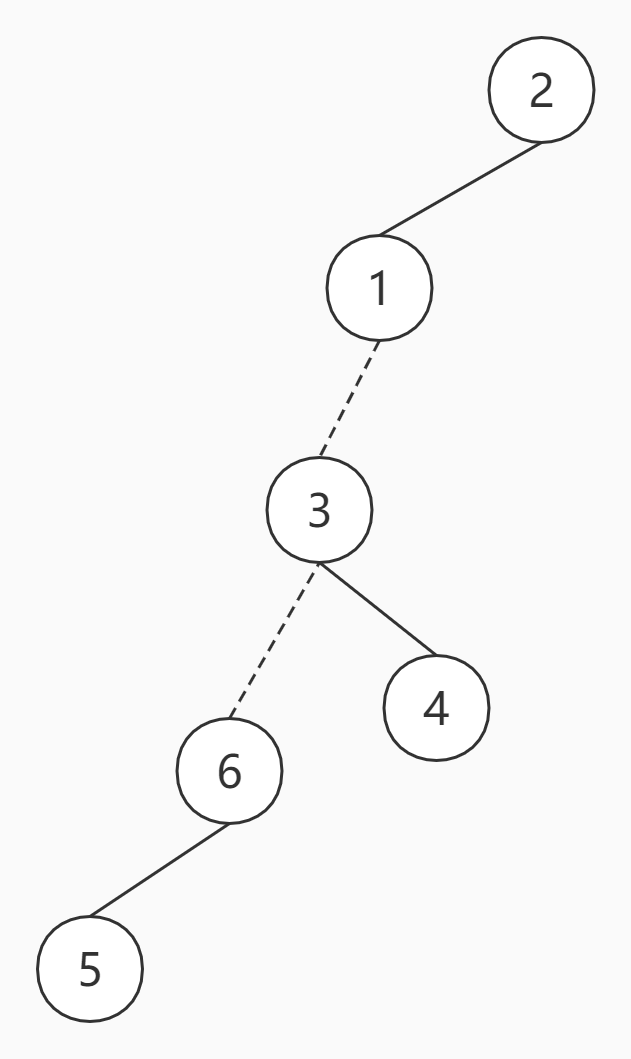
向6的父节点继续操作,把父节点3旋转到Splay的根节点
断开右子节点,也就是原来实边连向的4,然后连向上一个操作的Splay的根节点,也就是6(连向4的边改为虚边,连向6的边改为实边)
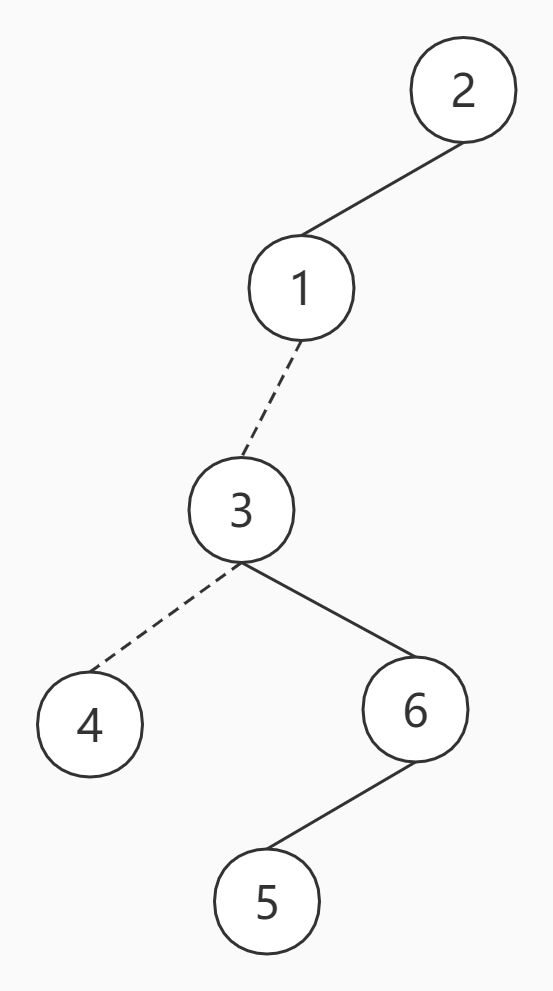
这里和上面一样,先把1旋转到根节点,把右子节点断开连向3
操作方法
将x点旋转到Splay的根节点
然后右节点断开,连向上一个操作的Splay的根节点(初始x连向0)
然后继续向x点的父节点进行操作(这里Splay树根节点的父亲存放的是深度最小的点在原树中的父亲,也就是最“左”的点在原树中的父亲)
代码
void access(int x)
{
for (int y = 0; x; y = x, x = fa[x])//x是当前操作的点,y是上一个操作的点,下一个操作的点是x的父亲节点
{
Splay(x);//先旋转到根节点
son[x][1] = y;//断开右节点,实边连向y,右节点连向y
push_up(x);//因为子树有变,所以要更新信息
}
return;
}
make_root
make_root(x)是将x设为原树根节点
例子
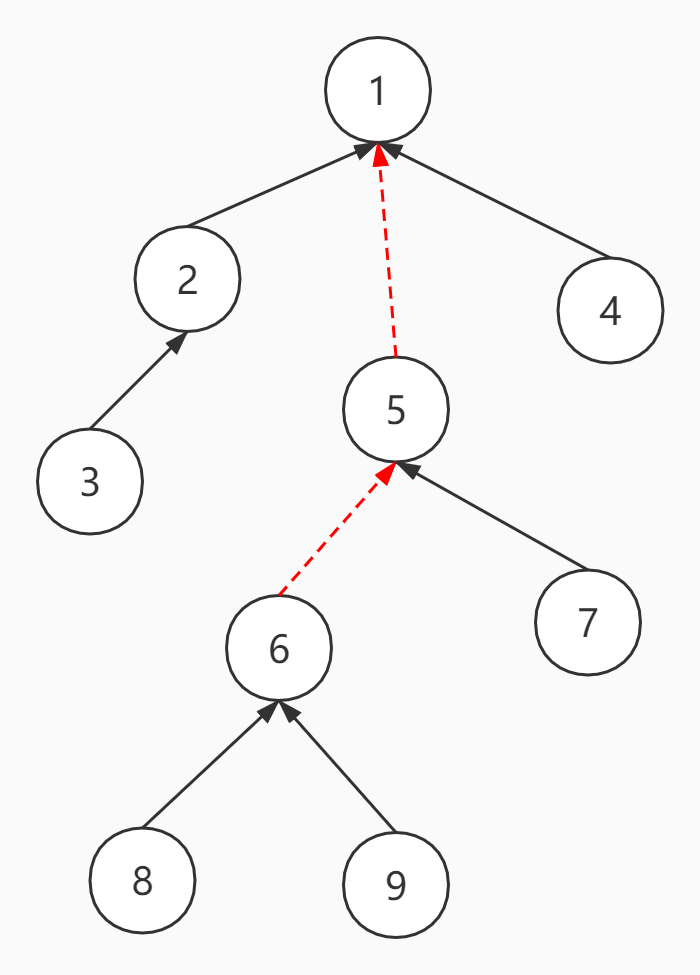
如下图,有向边连向父亲,那么根节点就是沿着边走到最后的点
此时进行make_root(6),就是要使所有点沿着边走最后到6
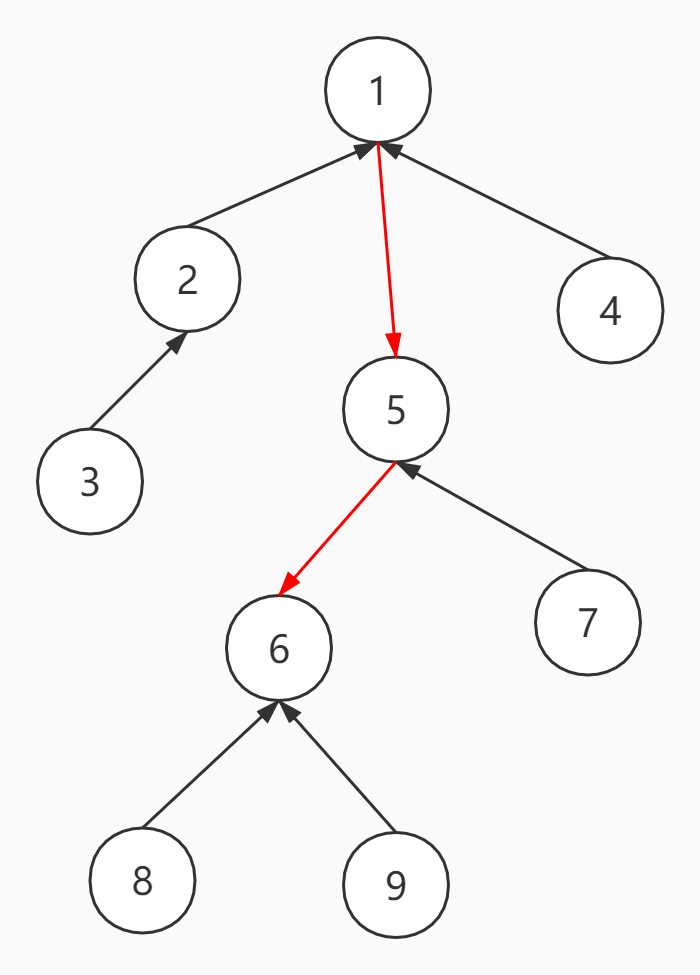
那么可以对6到当前根节点1的路径取反,这样就得到了我们要的结果
取反后所有点沿着边最终都到6,这就使6成为根节点
操作方法
对于边的取反就是使x节点到当前根节点路径上的父子关系全部取反(就如上面,取反前5是6的父亲,现在6是5的父亲)
首先要access(x),提取到根节点的路径
然后将当前节点旋转到Splay的根节点
然后使Splay上的所有点左右节点取反(即原来比x浅一层的变成比x深一层,以此类推),这样就实现了边的取反
对于左右节点取反可以用一个标记记下来,当要用时再向下传递,这样使时间复杂度有所下降(不需要用的点如果取反两次,就抵消了)
代码
void make_root(int x)
{
access(x);//提取路径
Splay(x);//旋转至根节点
push_rev(x);//交换左右子节点
return;
}
push_down
push_down(x)是下传x的标记,其中可能有make_root旋转的标记,也可能有修改的标记
代码
void push_rev(int x)//下传标记
{
swap(son[x][0], son[x][1]);//交换左右子节点
p[x] ^= 1;//打标记
return;
}
void push_down(int x)
{
if (p[x])//有标记
{
if (son[x][0]) push_rev(son[x][0]);//下传
if (son[x][1]) push_rev(son[x][1]);
p[x] = 0;//清空
}
return;
}
void push_hall(int x)
{
if (NR(x)) push_hall(fa[x]);//递归,先下传深度小的
push_down(x);
}
find_root
find_root(x)操作就是搜索x所在树的根节点
操作方法
先access(x),提取出路径
然后Splay(x),把x旋转至Splay的根节点
然后寻找最“左”的节点即可(深度最小的点)
代码
int find_root(int x)
{
access(x);//提取根节点
Splay(x);//旋转到根节点
while(son[x][0]) push_down(x), x = son[x][0];//找最左端的点,同时下穿标记
Splay(x);//保证复杂度
return x;
}
Split
Split(x,y)是提取x到y的路劲,以便对该链进行操作
操作方法
先make_root(x),使x为原树的根节点
然后access(y),提取y到x的根节点
最后Splay(y),使y为Splay的根节点,便于直接操作
代码
void Split(int x, int y)
{
make_root(x);
access(y);
Splay(y);
return;
}
link
link(x,y)为建立一条由x连向y的边
操作方法
make_root(x),把x设为x所在树的根节点
然后把x的父亲设为y,即把x所在树设为y的子树
代码
void link(int x, int y)
{
make_root(x);
if (find_root(y) != x) fa[x] = y;//判断是否在同一树中
}
cut
cut(x,y)为切断x到y的连边
操作方法
make_root(x),把x设为根节点
然后判断y的原树中的父节点是否是x,如果是就直接断开
代码
void cut(int x, int y)
{
make_root(x);
if (find_root(y) == x && fa[y] == x && !son[y][0])//find_root先判断是否在同一树中,其中进行了access(y)和Splay(x),
//所以可以直接判断是否为父亲,没有右节点是保证两点之间没有其他点
{
fa[y] = son[x][1] = 0;//断开
push_up(x);//更新
}
}
模板
Link Cut Tree (luogu 3690)
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 100010
using namespace std;
int n, m, g, x, y, top, d[N], v[N], s[N], p[N], fa[N], son[N][2];
bool NR(int x)//判断是不是根节点
{
return fa[x] && (son[fa[x]][0] == x || son[fa[x]][1] == x);
}
bool IRS(int x)//是否是右儿子
{
return son[fa[x]][1] == x;
}
void push_rev(int x)
{
swap(son[x][0], son[x][1]);
p[x] ^= 1;
return;
}
void push_down(int x)
{
if (p[x])
{
if (son[x][0]) push_rev(son[x][0]);
if (son[x][1]) push_rev(son[x][1]);
p[x] = 0;
}
return;
}
void push_up(int x)
{
s[x] = s[son[x][0]] ^ s[son[x][1]] ^ v[x];
return;
}
void push_hall(int x)//递归版下传
{
if (NR(x)) push_hall(fa[x]);
push_down(x);
return;
}
void rotate(int x)//旋转
{
int y = fa[x], z = fa[y], k = IRS(x), g = son[x][!k];
if (NR(y)) son[z][IRS(y)] = x;
if (g) fa[g] = y;
son[x][!k] = y;
son[y][k] = g;
fa[x] = z;
fa[y] = x;
push_up(y);
return;
}
void Splay(int x)
{
//push_hall(x);
int y=x;
d[++top]=y;
while(NR(y)) y = fa[y], d[++top] = y;
while(top) push_down(d[top--]);
while(NR(x))
{
if (NR(fa[x]))
{
if (IRS(x) == IRS(fa[x])) rotate(fa[x]);
else rotate(x);
}
rotate(x);
}
push_up(x);
return;
}
void access(int x)
{
for (int y = 0; x; y = x, x = fa[x])
Splay(x), son[x][1] = y, push_up(x);
return;
}
void make_root(int x)
{
access(x);
Splay(x);
push_rev(x);
return;
}
int find_root(int x)
{
access(x);
Splay(x);
while(son[x][0]) push_down(x), x = son[x][0];
Splay(x);
return x;
}
void Split(int x, int y)
{
make_root(x);
access(y);
Splay(y);
return;
}
void link(int x, int y)
{
make_root(x);
if (find_root(y) != x) fa[x] = y;
return;
}
void cut(int x, int y)
{
make_root(x);
if (find_root(y) == x && fa[y] == x && !son[y][0])
{
fa[y] = son[x][1] = 0;
push_up(x);
}
return;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &v[i]);
while(m--)
{
scanf("%d%d%d", &g, &x, &y);
if (g == 0)
{
Split(x, y);
printf("%d\n", s[y]);
}
else if (g == 1) link(x, y);
else if (g == 2) cut(x, y);
else Splay(x), v[x] = y;
}
return 0;
}
例题
Tree II
在模板上加了乘的操作
题解:https://ssllyf.blog.csdn.net/article/details/114940390
树点涂色
把题目的树套入LCT进行操作
题解:https://ssllyf.blog.csdn.net/article/details/115026737
Matches Are Not a Child's Play
把题目定义的删除序列作为权值构造LCT,巧妙地调整树的结构

