斜率优化
斜率优化
对于形如\(f_i=min\left \{i+j+a_i+a_j\right \}\)的DP进行优化,使其时间复杂度降低一个\(n\)
模板
题目大意
有n个任务,每个任务有一个时间和费用系数,每批任务可以选择若干个任务,每处理一批任务之前有s的开机时间,这批任务所需时间即为所选任务的时间之和,且所选任务一起完成
对于第i个任务,其费用为完成时间乘费用系数
让你安排任务,使其费用总和最小
解题思路
对于该题,我们可以先列出朴素的DP方程(t为时间前缀和,c为费用系数前缀和)
对于a>b
若a对i的贡献>b对i的贡献
那么有:
那么如果满足上式就可以得到“a对i的贡献>b对i的贡献”
上述式子和斜率十分相像
我们把f看作y,把c看作x那么就得到了一张关于相邻的点连线的图(k为斜率)
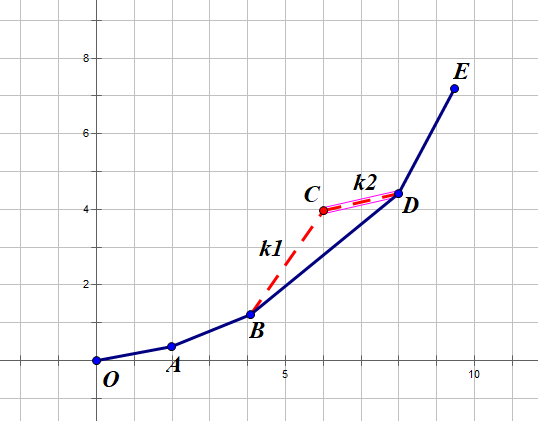
对于该图,\(k1>k2\)
对于某个i,若C为最优决策点,那么\(k1\leqslant s+t_i,k2>s+t_i\)
所以\(k1\leqslant s+t_i< k2\),与\(k1>k2\)不符,所以C为最优决策点不成立,所以把C给移除掉
由此可以得到:
我们要维护的是连续上升的k,也就是一个下凸的图,使得所有点都可能有用
维护这样一个图,只需在每次插入一个点时,拿i和i-1的连线与i-1和i-2的连线比较斜率,如果i和i-1的连线斜率较小,那么把i-1移去
对于决策点的选择,因为\(s+t_i\)是单调递增的,当第一条线斜率小于等于\(s+t_i\),就把第一个点和线给移除掉,这样移除后得到的所有线斜率都小于\(s+t_i\)所以第一个点就是最优决策点
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 5010
using namespace std;
int n, s, l, r, x[N], y[N], f[N], q[N], t[N], c[N];
int main()
{
scanf("%d%d", &n, &s);
for (int i = 1; i <= n; ++i)
{
scanf("%d%d", &t[i], &c[i]);
t[i] += t[i - 1];//前缀和
c[i] += c[i - 1];
}
memset(f, 127/3, sizeof(f));
f[0] = 0;//0点作为第一个点
q[1] = 0;
l = 1;
r = 1;
for (int i = 1; i <= n; ++i)
{
while(l < r && y[q[l + 1]] - y[q[l]] <= (s + t[i]) * (x[q[l + 1]] - x[q[l]])) l++;//把前面已经大于s*t的删掉
f[i] = f[q[l]] + s * (c[n] - c[q[l]]) + t[i] * (c[i] - c[q[l]]);//计算
x[i] = c[i];
y[i] = f[i];
while(l < r && (y[i] - y[q[r]]) * (x[q[r]] - x[q[r - 1]]) <= (y[q[r]] - y[q[r - 1]]) * (x[i] - x[q[r]]))//把不可能为决策点的点给删掉
r--;
q[++r] = i;//把当前点插进去
}
printf("%d", f[n]);
return 0;
}
例题
推荐题单
https://www.luogu.com.cn/training/5352#problems
例题1
锯木厂选址
先根据题意得到转移方程,然后解该方程,直接斜率优化DP即可(就是一道模板题,主要就是解方程不要出错)
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 20010
using namespace std;
ll n, l, r, sum, ans, q[N], w[N], d[N], y[N];
int main()
{
scanf("%lld", &n);
for (int i = 1; i <= n; ++i)
scanf("%lld%lld", &w[i], &d[i]);
for (int i = n - 1; i > 0; --i)
d[i] += d[i + 1];
for (int i = 1; i <= n; ++i)
sum += w[i] * d[i], w[i] += w[i - 1];
ans = sum;
for (int i = 1; i <= n; ++i)
{
while(l < r && (y[q[l + 1]] - y[q[l]]) > d[i] * (w[q[l + 1]] - w[q[l]])) l++;
ans = min(ans, sum - w[q[l]] * d[q[l]] - (w[i] - w[q[l]]) * d[i]);//找一个最优的结果
y[i] = w[i] * d[i];
while(l < r && (y[i] - y[q[r]]) * (w[q[r]] - w[q[r - 1]]) > (y[q[r]] - y[q[r - 1]]) * (w[i] - w[q[r]])) r--;
q[++r] = i;
}
printf("%lld", ans);
return 0;
}
例题2
任务安排
因为t(前缀和)不具有单调性,所以对左端点不能删去,取最优决策点时要二分查找
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
ll n, s, t, c, l, r, h, x[300010], y[300010], f[300010], q[300010], sumt[300010], sumc[300010];
ll find(ll ti)
{
ll L = 1, R = r;
while (L < R)//二分
{
ll mid = (L + R + 1) >> 1;
if (y[q[mid]] - y[q[mid - 1]] <= ti * (x[q[mid]] - x[q[mid - 1]])) L = mid;//判断两个点的优劣关系
else R = mid - 1;
}
return q[L];
}
int main()
{
scanf("%lld%lld", &n, &s);
for (int i = 1; i <= n; ++i)
{
scanf("%lld%lld", &t, &c);
sumt[i] = sumt[i - 1] + t;
sumc[i] = sumc[i - 1] + c;
}
memset(f, 127/3, sizeof(f));
f[0] = 0;
q[1] = 0;
l = 1;
r = 1;
for (int i = 1; i <= n; ++i)
{
h = find(sumt[i]);
f[i] = f[h] + s * (sumc[n] - sumc[h]) + sumt[i] * (sumc[i] - sumc[h]);
x[i] = sumc[i];
y[i] = f[i] - s * sumc[i];
while(l < r && (y[i] - y[q[r]]) * (x[q[r]] - x[q[r - 1]]) <= (y[q[r]] - y[q[r - 1]]) * (x[i] - x[q[r]]))//删除队列前面的点不影响,还是维护下凸包
r--;
q[++r] = i;
}
printf("%lld", f[n]);
return 0;
}

