网络流
网络流
一个网络G={V,E}是一张有向图,他的每一条边都有一个容量,图中还有一个源点(s)和汇点(t),源点可以流出无限流量,每一条边的流量不可以大于它的容量,这就是网络流
最大流
就是让你求到汇点的流量最大是多少
说明:
如果有一条从源点到汇点的路径上各条边的剩余容量都大于0,则称这条路径为一条增广路(出自蓝书)
以下介绍两种(蓝书上有的)算法
Edmonds-Karp算法
用bfs寻找每一条增广路,然后在这条增广路上流,直到这条增广路无法再流
重复这个操作,直到找不到增广路为止,这时到汇点的流量就是最大流
这里有一个要点:
我们先建立一个图(如下)
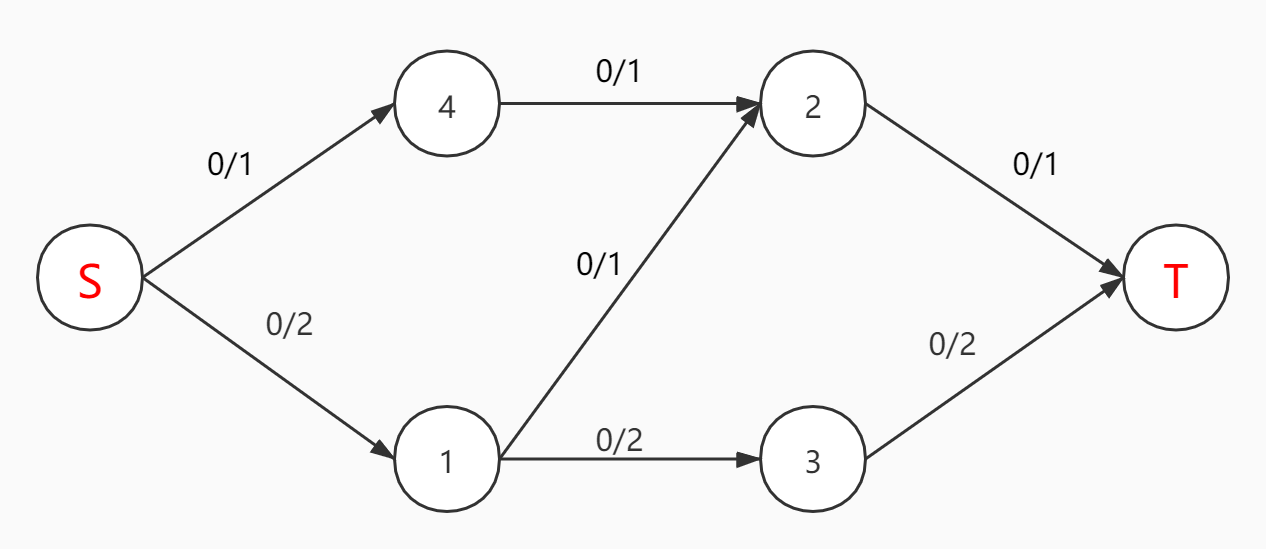
我们按字典序来搜索,首先会搜索到S->1->2->T
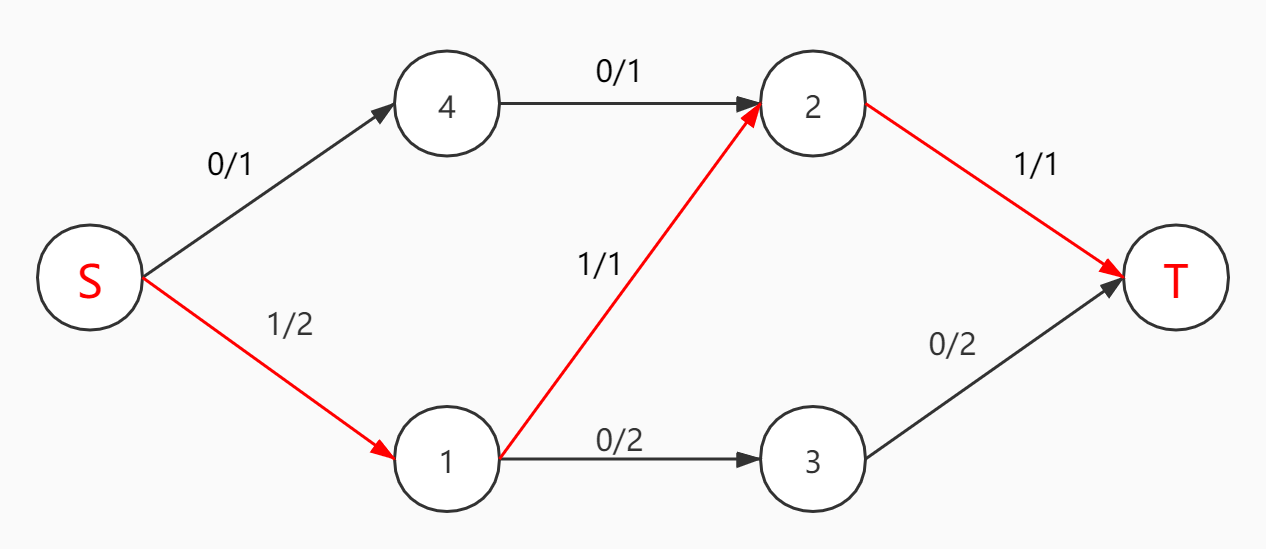
然后搜索到S->1->3->T
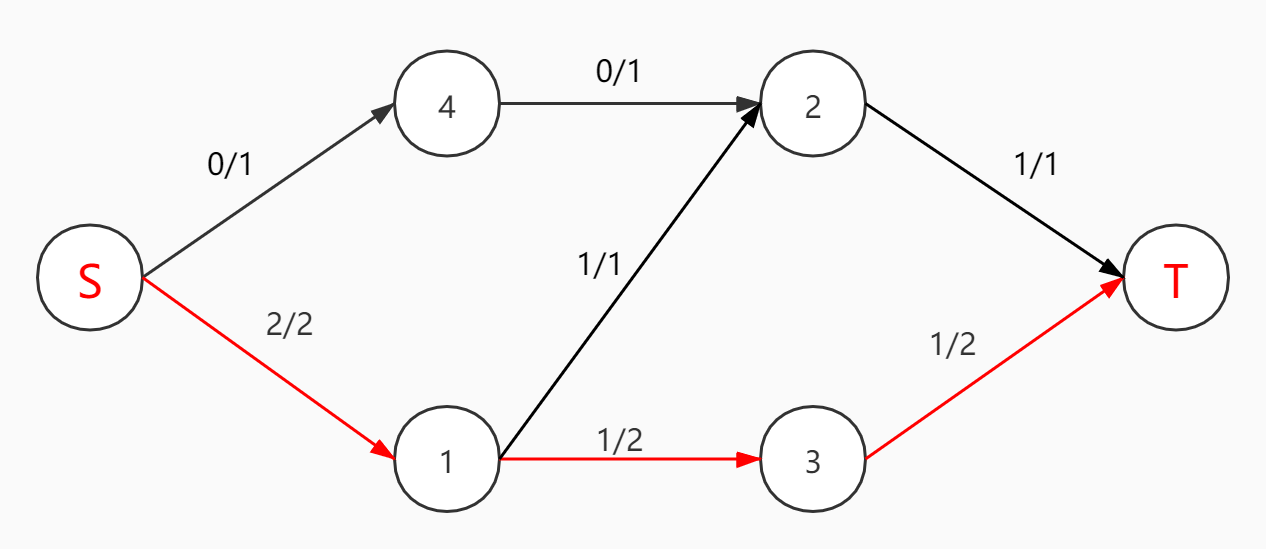
现在如果是正的边我们是无法找到增广路了,但是如果不看1->2这条边,那么我们可以流3
为了解决这种问题,我们要对于每一条正边建立一条逆边(我们设正边为x->y,那么逆边就是y->x),当正边流时,逆边的容量相应地增加这个流量,它的意义就是当有流到y时,我们让这个流代替先前x->y的流去完成它的路径,然后吧x->y撤回去,回到x继续去找增广路
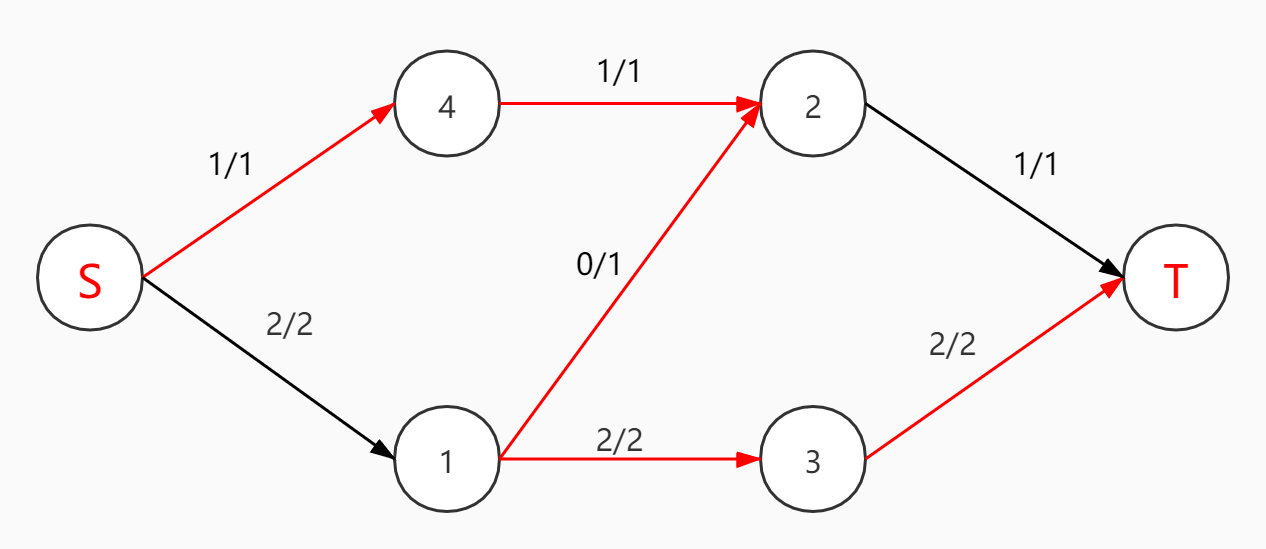
时间复杂度:\(O(n^2m)\)
因为Edmonds-Karp算法不太实用所以本蒟蒻没有去打
Dinic算法
在任意时刻,网络中所有节点以及剩余容量大于0的边构成的子图被称为残量网络(出自蓝书)
Edmonds-Karp算法每一次都可能遍历整个残余网络,而只找到一条增广路,我们可以用Dinic算法一次性找到所有长度相同的增广路(记住是长度相同),我们用一个dep来记录当前点到源点的距离,然后用bfs遍历,当我们找到第一条增广路时,别的长度相同的也会得到,我们后面用dep来遍历,我们走一条边必须要dep[y]=dep[x]+1这样就保证了不会多走,前面之所以说别的长度相同的增广路也会的到是因为:当我们遍历到T时,所有dep=dep[T]-1的都一定会先遍历到(bfs的性质),所以会都连上
时间复杂度:\(O(n^2m)\)~\(O(m \sqrt{n})\)
模板:
const int inf = 1 << 29;//一个很大的值
int tot = 1;//这里是1才能用异或来判断正逆边关系
struct rec
{
int to, next, edge;
}a[20000];
queue<int> d;
void add(int x, int y, int z)//连边
{
a[++tot].to = y;
a[tot].edge = z;
a[tot].next = head[x];
head[x] = tot;
a[++tot].to = x;//逆边
a[tot].edge = 0;//一开始没值
a[tot].next = head[y];
head[y] = tot;
}
bool bfs()//找增广路
{
memset(dep, 0, sizeof(dep));
while(!d.empty()) d.pop();
d.push(s);
dep[s] = 1;
while (!d.empty())
{
int h = d.front();
d.pop();
for (int i = head[h]; i; i = a[i].next)
if (!dep[a[i].to] && a[i].edge)//有残余流量且未遍历过
{
dep[a[i].to] = dep[h] + 1;//计算dep
if (a[i].to == t) return true;//到达汇点
d.push(a[i].to);
}
}
return false;
}
int dinic(int x, int flow)//rest是已流多少,flow是最小残余流量
{
if (x == t) return flow;
int rest = 0, k;
for (int i = head[x]; i; i = a[i].next)
if (dep[x] + 1 == dep[a[i].to] && a[i].edge)
{
k = dinic(a[i].to, min(a[i].edge, flow - rest));
if (!k) dep[a[i].to] = 0;//如果流不了那就不可能再流了
rest += k;//总流量
a[i].edge -= k;//正边残余流量减去流量
a[i^1].edge += k;//逆边相加
if (rest == flow) return rest;//已留完
}
return rest;
}
int main()
{
...
add(x, y, z);
...
while (bfs())//找得到增广路
ans += dinic(s, inf);//因为要取min所以初始值是inf
...
}
模板题:
应用:
网络流可以用于二分图的最大匹配,
对于一个二分图:
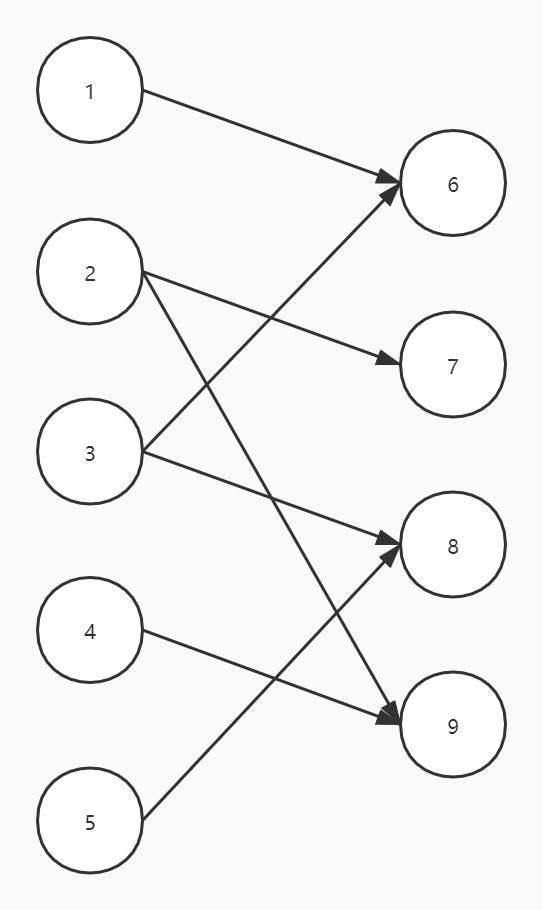
我们可以把它建成以下的图,即S与左边的每个点连上,右边的每个点与T连上(容量都为1),现在求得最大流就是二分图的最大匹配,如果某个点可以选择多遍,那么直接把与S或T相连的边容量相加即可
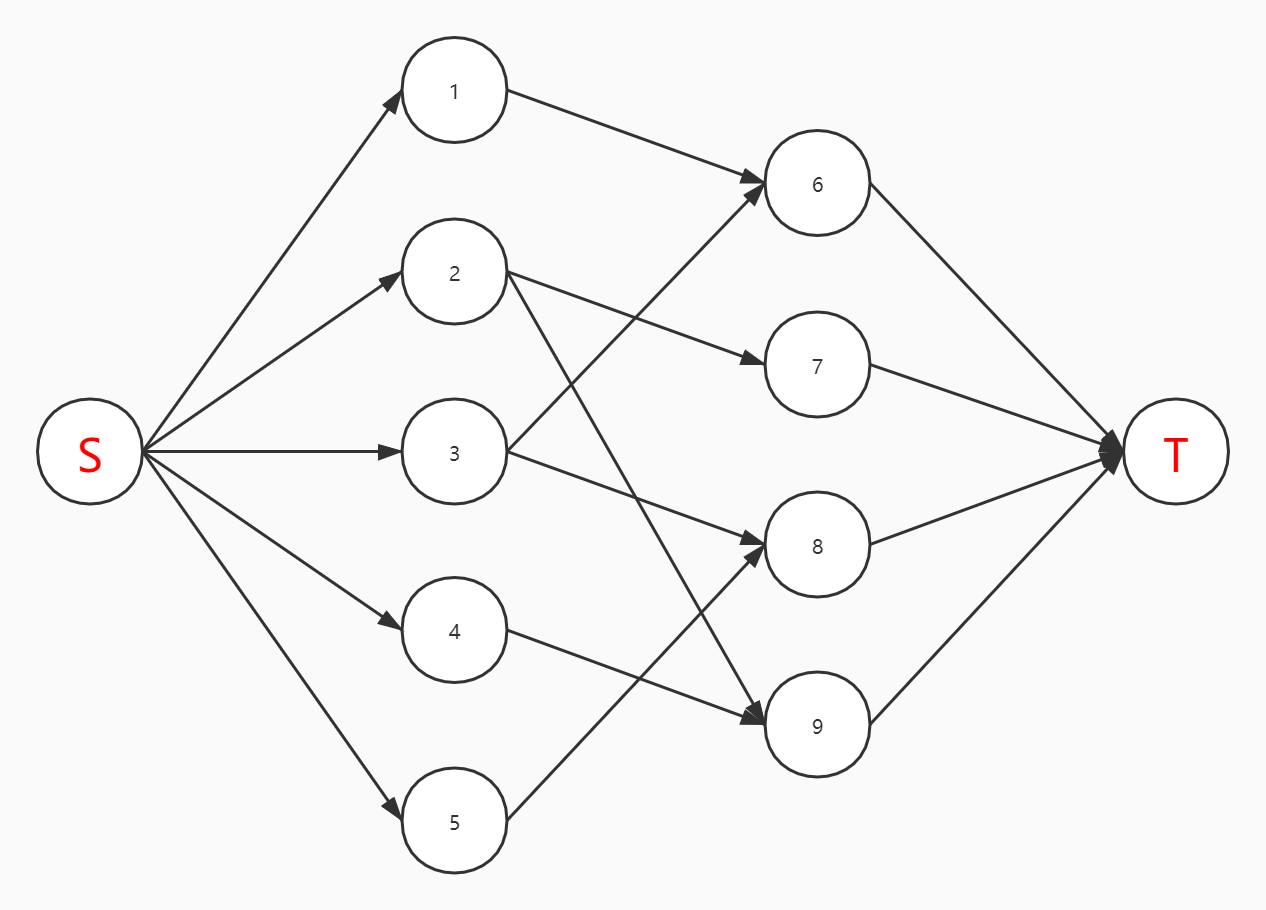
例题:牛棚安排(gmoj 1259)
题解:https://blog.csdn.net/ssllyf/article/details/103999202
费用流
在网络流的基础上给每一条边都加上了一个费用,当一个流经过这条边时,总费用就加上这条边的费用,现在让你求在最大流的前提下,最小费用是多少
Edmonds-Karp算法
我们可以“把每一次找一条增广路”改为“每一次找总费用最小的增广路”,这样可以使每一次从源点流向汇点的费用最小,也就保证了总费用最小
找费用最小的增广路用最短路的方法求即可
时间复杂度:\(O(n^2mK)\)
模板
const int inf = 1<<29;
struct rec
{
int to, f, edge, next;
}a[100500];
void add(int x, int y, int z, int o)
{
a[++tot].to = y;
a[tot].next = head[x];
head[x] = tot;
a[tot].edge = z;
a[tot].f = o;
a[++tot].to = x;
a[tot].next = head[y];
head[y] = tot;
a[tot].edge = 0;
a[tot].f = -o;//费用相反,因为撤回费用要减去
}
bool spfa()
{
memset(b, 127/3, sizeof(b));//费用一开始要很大才能搜下去
memset(l, 0, sizeof(l));
queue<int>d;
o = b[0];
b[s] = 0;
l[s] = inf;//源点无限流量
d.push(s);
while(!d.empty())
{
h = d.front();
d.pop();
for (int i = head[h]; i; i = a[i].next)
if (b[h] + a[i].f < b[a[i].to] && a[i].edge)
{
b[a[i].to] = b[h] + a[i].f;//费用
l[a[i].to] = min(l[h], a[i].edge);//流量
last[a[i].to] = i;//连接上一个点的边
if (!p[a[i].to])
{
p[a[i].to] = 1;
d.push(a[i].to);
}
}
p[h] = 0;
}
return b[t] != o;
}
void dfs()
{
x = t;
while(last[x])
{
a[last[x]].edge -= l[t];//剩余流量调整
a[last[x]^1].edge += l[t];
x = a[last[x]^1].to;//倒着回去
}
ansf += b[t] * l[t];//总费用
ans += l[t];//总流量
return;
}
int main()
{
...
add(x, y, z, o);//加边
...
while(spfa())//找得到
dfs();//流
...
}

