Programming Languages PartA Week5学习笔记——SML进阶与编程哲学

@

目录

• Week5 Introduction
• What is Type Inference
• ML Type Inference
• Type Inference Examples
• Polymorphic Examples
• Optional: The Value Restriction and Other Type-Inference Challenges
• Mutual Recursion
• Modules for Namespace
• Signatures and Hiding Things
• A Module Example
• Signatures for Our Example
• Signature Matching
• An Equivalent Structure
• Another Equivalent Structure
• Different Modules Define Different Types
• Equivalent Functions
• Standard Equivalences
• Equivalence Versus Performance

Week5 Introduction

第五周内容的简单导引

What is Type Inference

关于type-checking。ML属于静态类型语言（虽然在编写代码时并不要求显式标出变量类型），在编译时会判断变量类型。

所以ML语言其实是一种隐含类型(Implicitly typed)的静态类型语言

类型推断，为每个bingding或者表达式给定一个类型，这样就判断type-chcking成功

ML Type Inference

ML的类型推断

类型推断的关键步骤：

类型推断的简单例子：

ML中为无法判断的类型给定一个Type Variable （例如 'a, 'b，可用于实现多态）。但需要注意的是并不是所有type inference的语言都有type variable（例如Java），有type variable的语言也不一定会做type inference

Type Inference Examples

类型推断始终遵循几大步骤（与上一节相同的步骤）

1、按照顺序收集所有binding，并决定类型

2、对于每个binding（变量或者表达式或者函数等）

（1）收集所有类型检查需要的事实，分析约束条件（Constraints）来确定类型

（2）类型的事实有冲突，抛出type error （Over-Constrained）

（3）对没有事实可以判断类型的binding给定一个type variable （Unconstrained）

其中2-(1)是本节阐述的内容，如何通过事实分析约束条件

例子1：

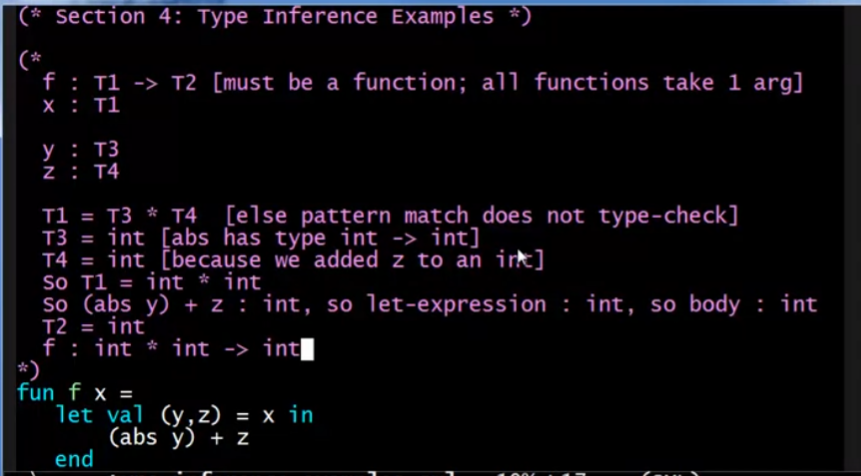
例子2：

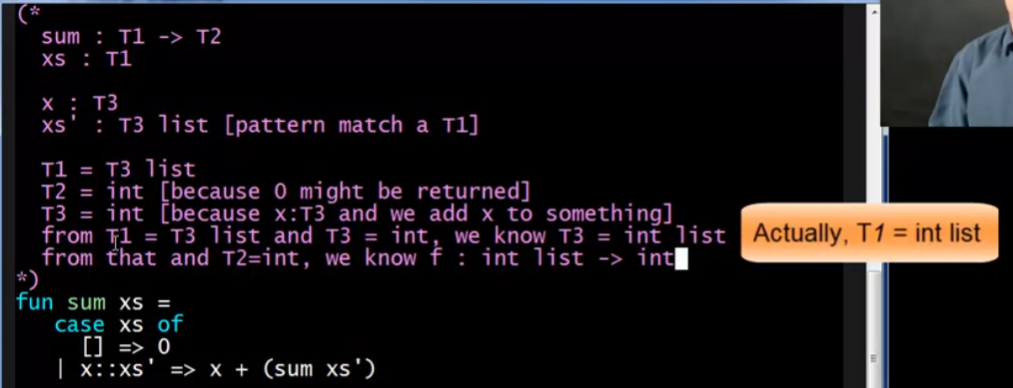
Polymorphic Examples

多态的例子，首先仍然是同样的判断准则：

例子1

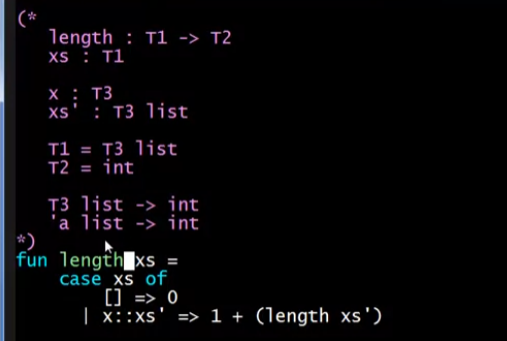
例子2，T4存在两种情况，因为编译器不知道会执行哪一条语句，只知道type的可能性。只有在运行时才能确定执行哪条语句。

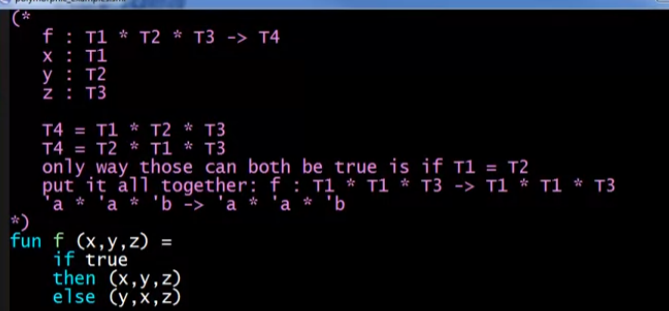
例子3：

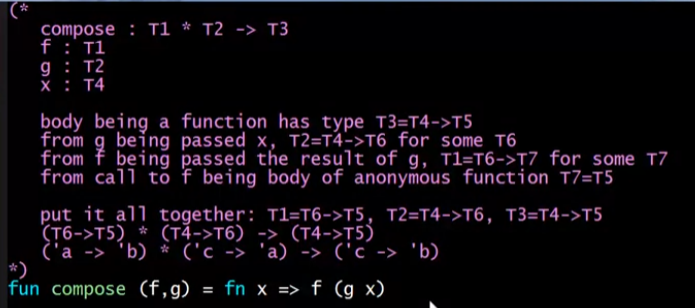
Optional: The Value Restriction and Other Type-Inference Challenges

截至目前，课程讲述的ML 类型推断体系是不完全的，但想要让它更完善就不得不引入更高级但更不优雅的内容

例如如下问题：

我们不能只是为reference类型制定特殊规则来避免这个问题，因为ML的函数可传递，同时类型又可以取别名，type-checker不知道reference的别名（type-chekcer在运行之前检查）。

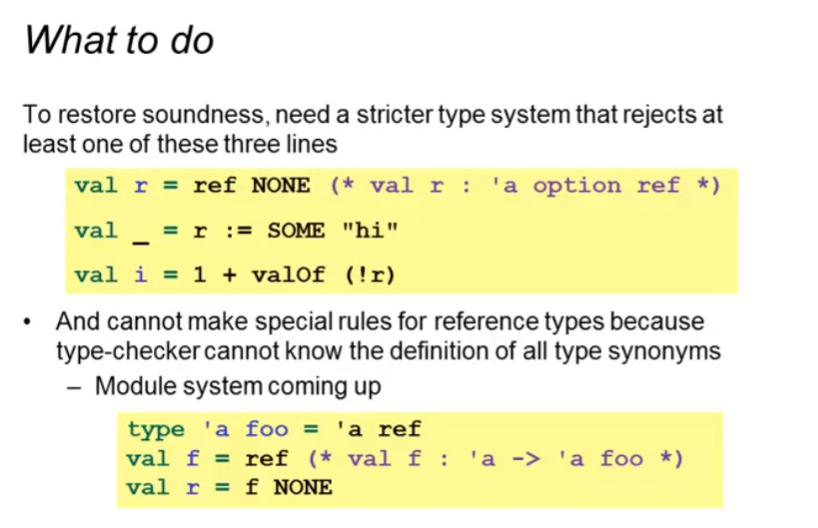
解决方案是为整个语言引入Value restriction的机制，只让变量binding（变量或者值的表达式或者函数定义时）获得多态类型，但函数调用不能获得多态类型（会给出一个警告和无约束的假类型）：

当编译器无法判断是否有reference参加或者是否生成reference的时候，也会使用value restriction

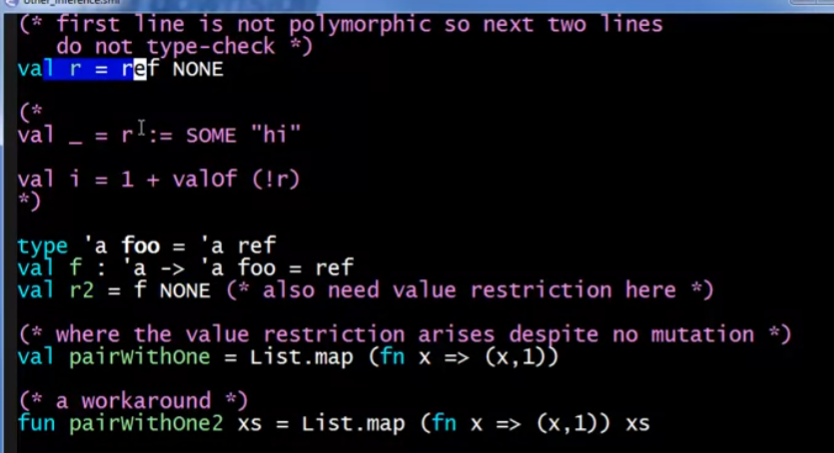
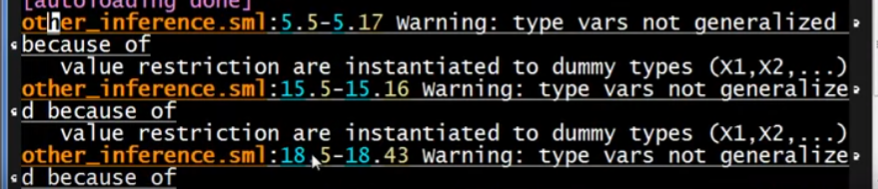
关于子类型的讨论，子类型 所实现的多态（类似于其他语言中子类和超类的关系，例如超类指针指向子类地址），在一定的细节约束下也可以支持，但会让语言中的类型更难以推断和理解（所以在C++和Java这类静态类型语言中需要显式声明变量的类型）

Mutual Recursion

互递归就是两个函数相互调用，有一定用处，例如可以实现状态机，但也会带来一些问题（由于相互调用，难以分清binding的先后顺序）：

ML的做法是定义一套新的结构，使用and关键词来连接多个函数或datatype（因为datatype定义时也可以递归定义）等，这些使用and连接的变量将会作为一个整体（bundle），同时被type-check或valuate

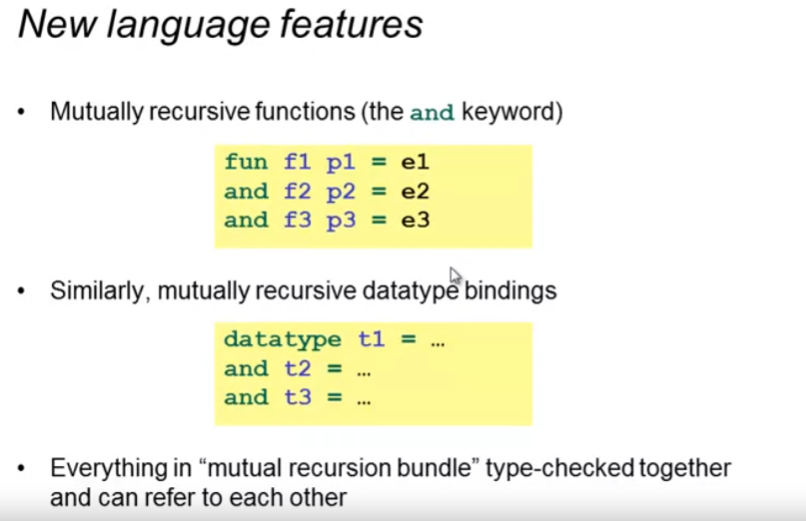
例子：

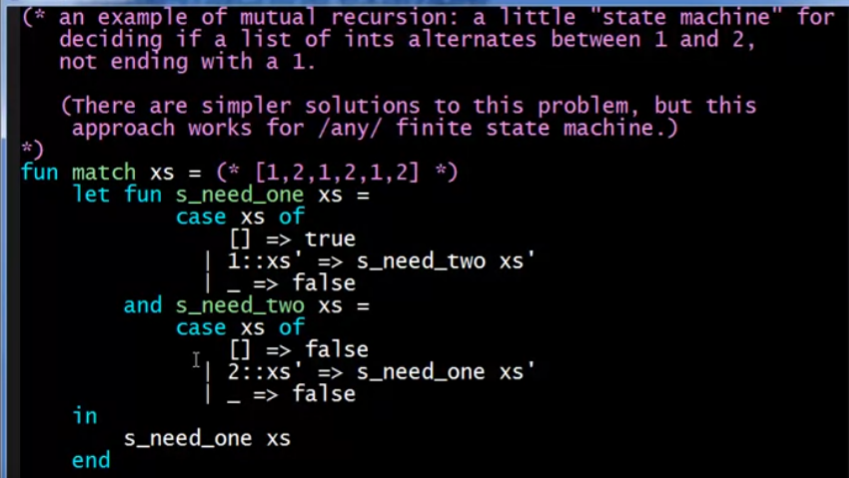
第二个例子：

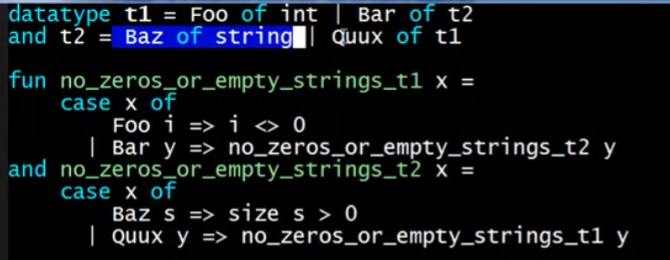
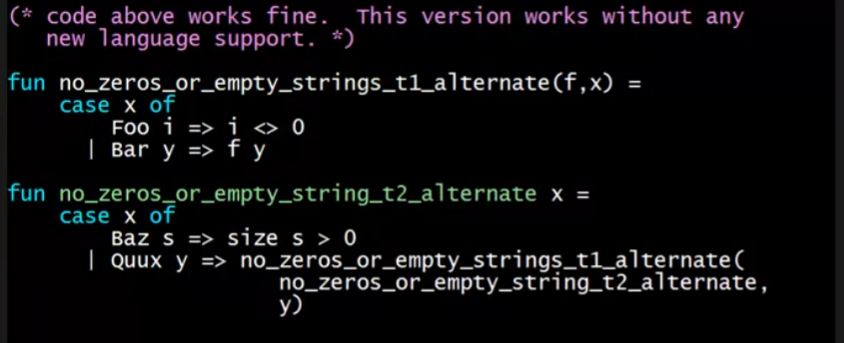
同时，也可以使用高等函数（传递一等函数）来替代and结构，实现同样的功能

Modules for Namespace

使用structure关键词定义modules 。modules的概念在ML中类似于C++的命名空间和类的混合概念（可以用来定义ADT，见后面的例子）。

例子:

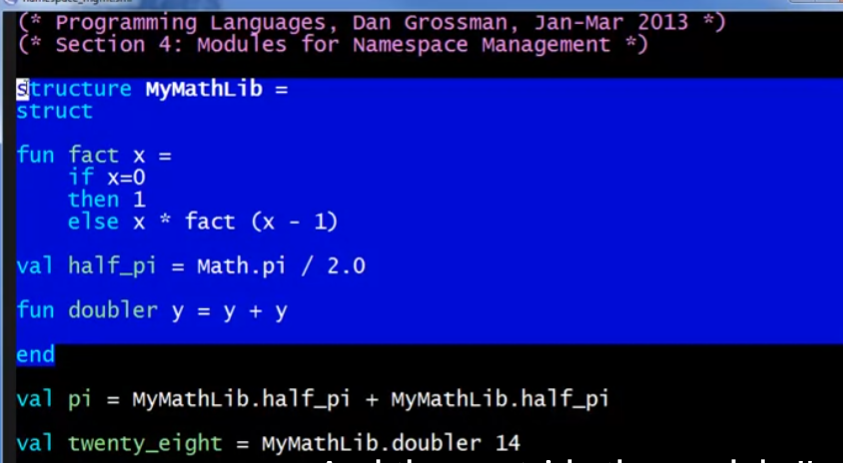
open关键词用于直接引入一个module，可以不带module名直接使用其中的bindings（类似python的 from xxx import *)。也可以通过函数传递的方式，将module的某个函数binding到某个变量上，直接使用。

Signatures and Hiding Things

Signature是module的一种类型，其中定义有哪些binding与binding的类型，可以通过 :> 符号作用于module。（这里的signature和module又有点像Java的接口和类的关系了，但也不太一样）。

** signatures的真正价值是用来隐藏某些bindings及其类型的定义，并对外隐藏实现细节（从这个意义上来说，signatures实际上也确实类似接口的功能）。

通过signatures我们可以实现private和public的bindings。

• 在signatures中定义的bindings可以在module外部使用（public）
• 不在signatures中定义的bindings 不能在module外部使用，但可以在内部使用（private）

A Module Example

定义一个ADT，表示实数及其运算

(* Section 4: A Module Example *)

(* will assign different signatures to this module in later segments *)

structure Rational1 = 
struct

(* Invariant 1: all denominators > 0
   Invariant 2: rationals kept in reduced form *)

  datatype rational = Whole of int | Frac of int*int
  exception BadFrac

(* gcd and reduce help keep fractions reduced, 
   but clients need not know about them *)
(* they _assume_ their inputs are not negative *)
  fun gcd (x,y) =
       if x=y
       then x
       else if x < y
       then gcd(x,y-x)
       else gcd(y,x)

   fun reduce r =
       case r of
	   Whole _ => r
	 | Frac(x,y) => 
	   if x=0
	   then Whole 0
	   else let val d = gcd(abs x,y) in (* using invariant 1 *)
		    if d=y 
		    then Whole(x div d) 
		    else Frac(x div d, y div d) 
		end

(* when making a frac, we ban zero denominators *)
   fun make_frac (x,y) =
       if y = 0
       then raise BadFrac
       else if y < 0
       then reduce(Frac(~x,~y))
       else reduce(Frac(x,y))

(* using math properties, both invariants hold of the result
   assuming they hold of the arguments *)
   fun add (r1,r2) = 
       case (r1,r2) of
	   (Whole(i),Whole(j))   => Whole(i+j)
	 | (Whole(i),Frac(j,k))  => Frac(j+k*i,k)
	 | (Frac(j,k),Whole(i))  => Frac(j+k*i,k)
	 | (Frac(a,b),Frac(c,d)) => reduce (Frac(a*d + b*c, b*d))

(* given invariant, prints in reduced form *)
   fun toString r =
       case r of
	   Whole i => Int.toString i
	 | Frac(a,b) => (Int.toString a) ^ "/" ^ (Int.toString b)

end

Signatures for Our Example

使用signatures，隐藏上一节的例子中的gcd和reduce，将bindings私有化

但是只隐藏函数当然会有问题，我们的变量并没有得到有效封装（暴露给了用户），用户可以通过例如Rationall.Frac(1,0)来自己产生这个变量。我们应该把这些部分封装起来。

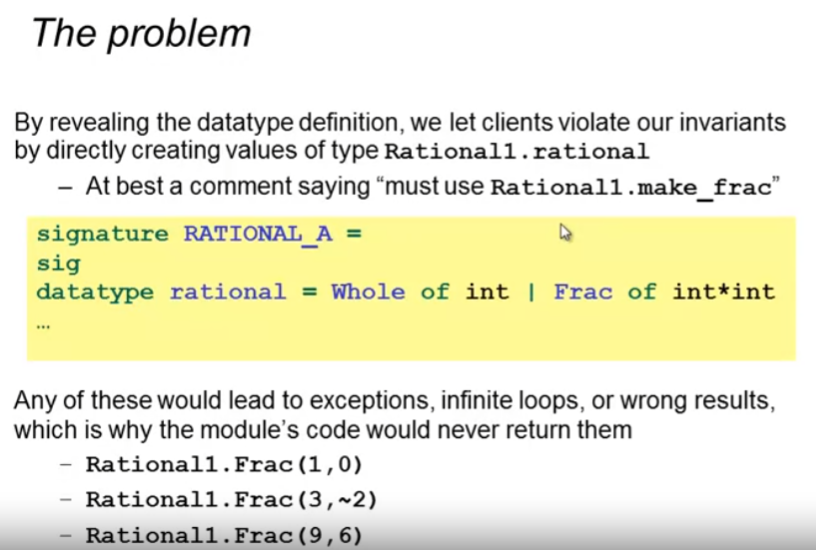
所以需要将内部datatype定义的类型一并设为私有，并留出给用户定义变量的接口 make_frac。但问题在于signatures中开放的函数需要用到datatype定义的rational类型，但现在signatures不知道它存在。

要解决这个问题，ML中可以通过type关键词在signatures中标明某种类型的存在（一种抽象类型），但不开放给用户（用户不知道其定义）

因此，使用signatures的两大关键在于：

另外，比较有趣的事情是，由于Whole不会引发异常带来问题，我们也可以对用户开放Whole（相当于开放rational的一部分），记得datatype的Constructor本身就是一个函数，所以我们可以直接在signatures中写上Whole函数的部分，而不需要在module中重复定义（因为定义datatype的时候已经写了datatype rational = Whole of int | Frac of int*int，Whole在这里就会被认为是一个int->rational的函数定义）

Signature Matching

An Equivalent Structure

抽象的一大目的是让不同实现（implementation）相等（equivalent）（对用户而言），例如接口的抽象也是需要让类实现对用户等效。用户不关心具体实现细节，但相同的接口（即使实现不同），也应该得到等效的结果。

例如，以前面的三种RATIONAL signatures为例：

老师给出的例子：

(* Section 4: An Equivalent Structure *)

(* this signature hides gcd and reduce.  
That way clients cannot assume they exist or 
call them with unexpected inputs. *)
signature RATIONAL_A = 
sig
datatype rational = Frac of int * int | Whole of int
exception BadFrac
val make_frac : int * int -> rational
val add : rational * rational -> rational
val toString : rational -> string
end

(* the previous signature lets clients build 
 any value of type rational they
 want by exposing the Frac and Whole constructors.
 This makes it impossible to maintain invariants 
 about rationals, so we might have negative denominators,
 which some functions do not handle, 
 and print_rat may print a non-reduced fraction.  
 We fix this by making rational abstract. *)
signature RATIONAL_B =
sig
type rational (* type now abstract *)
exception BadFrac
val make_frac : int * int -> rational
val add : rational * rational -> rational
val toString : rational -> string
end
	
(* as a cute trick, it is actually okay to expose
   the Whole function since no value breaks
   our invariants, and different implementations
   can still implement Whole differently.
*)
signature RATIONAL_C =
sig
type rational (* type still abstract *)
exception BadFrac
val Whole : int -> rational 
   (* client knows only that Whole is a function *)
val make_frac : int * int -> rational
val add : rational * rational -> rational
val toString : rational -> string
end 

(* this structure can have all three signatures we gave
   Rationa1 in previous segments, and/but it is 
   /equivalent/ under signatures RATIONAL_B and RATIONAL_C 

   this structure does not reduce fractions until printing
*)
       
structure Rational2 :> RATIONAL_A (* or B or C *) =
struct
  datatype rational = Whole of int | Frac of int*int
  exception BadFrac

   fun make_frac (x,y) =
       if y = 0
       then raise BadFrac
       else if y < 0
       then Frac(~x,~y)
       else Frac(x,y)

   fun add (r1,r2) = 
       case (r1,r2) of
	   (Whole(i),Whole(j))   => Whole(i+j)
	 | (Whole(i),Frac(j,k))  => Frac(j+k*i,k)
	 | (Frac(j,k),Whole(i))  => Frac(j+k*i,k)
	 | (Frac(a,b),Frac(c,d)) => Frac(a*d + b*c, b*d)

   fun toString r =
       let fun gcd (x,y) =
	       if x=y
	       then x
	       else if x < y
	       then gcd(x,y-x)
	       else gcd(y,x)

	   fun reduce r =
	       case r of
		   Whole _ => r
		 | Frac(x,y) => 
		   if x=0
		   then Whole 0
		   else
		       let val d = gcd(abs x,y) in 
			   if d=y 
			   then Whole(x div d) 
			   else Frac(x div d, y div d) 
		       end
       in 
       (* 注意这里调用的reduce，Rational1中没有reduce *)
	   case reduce r of
	       Whole i   => Int.toString i
	     | Frac(a,b) => (Int.toString a) ^ "/" ^ (Int.toString b)
       end
end

可以发现，如果给用户过多的权限（例如在signatures中定义了rational类型，用户能直接调用Frac构造器）就会导致如下的不同实现中结果不相等的情况，这样的抽象就不是一个好的抽象。所以将rational在signature中作为一个抽象类型是非常重要的。

结论是：当signature的公共接口暴露的越少（抽象程度越高），不同实现对用户的呈现结果越可能实现equivalent。

Another Equivalent Structure

不同的structures可以为signature中的抽象类型提供不同实现，例如让type rational = int * int

注意第二点细节，虽然signature规定Whole需要int -> rational，但这是对外部而言（signature规定都是对外部而言），在内部由于目前的例子中Whole没有定义，所以可以自行定义，甚至可以实现多态'a -> 'a * int（在内部调用时），但在外部就必须是int->int*int ,也就是目前的int -> rational

Different Modules Define Different Types

即使是实现了同一个signature的modules，不同的实现都定义了不同的类型。

例子，当多个不同的modules相互调用时会抛出异常，这也很容易理解（毕竟module首先具有命名空间的作用，每个module内部函数生成的内部变量都要带上一个命名空间的前缀，例如Rational3.rational）

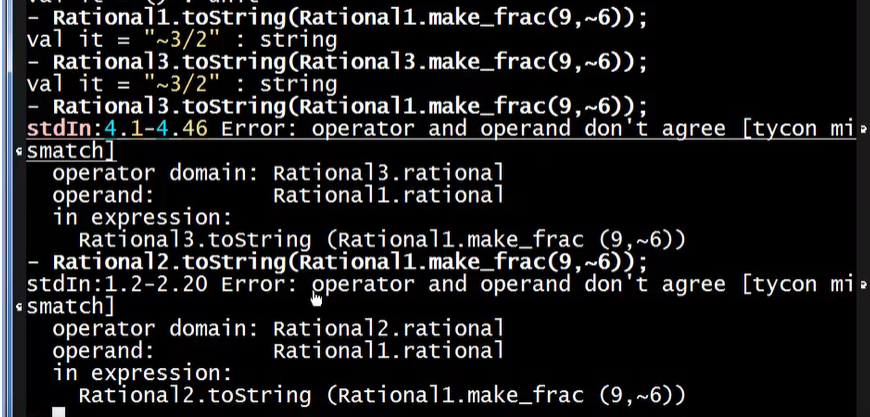
从这些模块的函数类型可以看出，不同的模块就是不同的类型

Equivalent Functions

为什么我们需要Equivalence

（1）为了代码维护或重构

（2）为了代码迭代向下兼容

（3）为了优化代码运行效率

（4）为了代码抽象

例如我们需要在重构垃圾代码时保持函数功能（包括接口）不变，这就是一种Equivalence

两个函数什么时候能够实现等效？在他们在任何地方都拥有观察起来相同的行为的时候

这里注意一下副作用（side-effect），在函数式编程中，我们尽可能让所有的函数都定义成实现一种类似于数学函数的行为模式（接受自变量，返回因变量），而没有多余的操作。这些多余的操作，例如在函数中（不是通过返回值shadowing的方式）改变某个变量的现有值（mutation），读取设备或文件等的输入或者向设备或文件输出（input/output），抛出异常和处理异常（exception raise and handle）等，都相当于是函数的副作用。

纯粹的函数更可能让事物（让更多事物）等效（Pure functions make more things equivalent）

Standard Equivalences

其他一些标准的等效情况

（1）先是语法糖 andalso orelse之类的等效

（2）然后是替换函数内部的一些参数名

（3）是否使用helper function不影响等效情况（在使用的函数的scope没改变的情况下）

（4）不必要的function wrapping不影响等效

值得注意的是，下面例子中的反例，左侧g会表现为定义时不会print（因为是函数定义，不会调用），但调用时print every time，右侧g表现为定义（实际上不是定义函数，而是传递(h())的调用结果）时print一次，之后调用不会再print

(5) 在忽略类型的时候，下面的两种表达式等效（let 和 匿名函数）

但事实上两者的类型不同，左侧的x可以多态，而右侧不可。右侧的涵盖范围相对小一些。（why？这里其实没太理解）

Equivalence Versus Performance

Equivalence虽然是外部表现相同，但由于内部实现不同，会导致运行表现上的差异（例如时间、空间差异）。这也是为什么我们能够优化代码效率（内部）并保持Equivalence（外部）。

为不同的任务定义不同的等效定义：