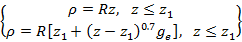MATLAB地图工具箱学习心得(二)设计可变参数和位置拾取的“放大镜”式投影程序
最近刚好因为一些原因整理这方面的内容,所以还是把这篇鸽了一年多的博客顺手写出来了∠( ᐛ 」∠)_。因为是当时课程设计的一部分,程序上难免会有一些不足和bug,在这里将设计的思路分享给大家。
本篇博客的代码可以在我的github项目中查看:https://github.com/NewBearEar/Magnifying-azimuthal
关于matlab地图投影系列:
一、定义坐标变换的方程
首先在matlab安装目录E:\MATLAB2016a\toolbox\map\mapproj\private\位置找到在方位投影中进行坐标变换的函数applyAzimuthalProjection.m,即在对应如图所示函数的应用之下,它将方位投影函数中的大地坐标转换为球面极坐标。
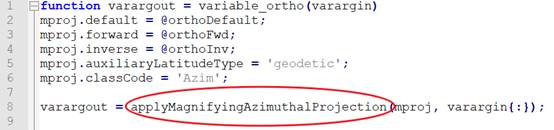
于是为了实现放大镜效果,可以利用如下公式对方位角进行判断,从而得到“放大镜”式的等距离方位投影效果。
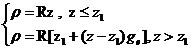
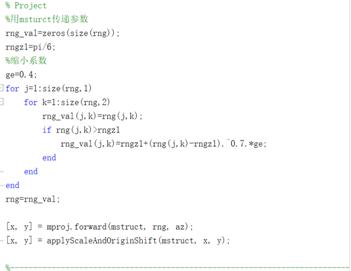
为了实现该公式,并且不改变原有的mappingtoolbox工具箱结构,将applyAzimuthalProjection.m的内容复制作为applyMagnifyingAzimuthalProjection函数(applyMagnifyingAzimuthalProjection.m文件),并在其applyForward函数中添加如下代码,实现“放大镜”式的等距离方位投影的坐标变换公式:
%用msturct传递参数
rng_val=zeros(size(rng));
rngz1=mstruct.rngz1;
%缩小系数
ge=mstruct.zoom_factor;
for j=1:size(rng,1)
for k=1:size(rng,2)
rng_val(j,k)=rng(j,k);
if rng(j,k)>rngz1
rng_val(j,k)=rngz1+(rng(j,k)-rngz1).*ge;
end
end
end
rng=rng_val;
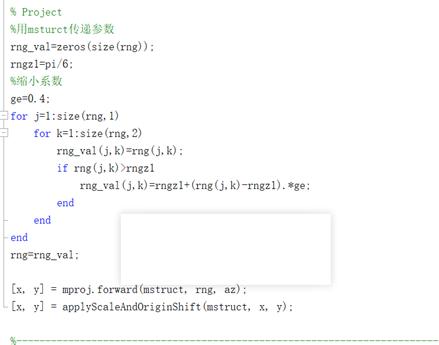
但值得注意的是,有时mappingtoolbox工具箱可能会对新添加的private函数(如applyMagnifyingAzimuthalProjection函数)产生找不到函数的问题,如果出现这种情况就只能直接修改工具箱的applyAzimuthalProjection.m的内容了。
二、通过mstruct传递自定义参数
(1)由于matlab的mappingtoolbox的任意一个投影都是通过mstruct定义包括投影中心,旋转情况,标准纬线等属性,在调用投影变换时也是直接传入 mstruct 并调用一些相应的方法(由于 msturct 只是一个结构体,而不是类,其方法与结构体本身是分离的,所有大多数方法都是传入一个 mstruct 作为参数)
E:\MATLAB2016a\toolbox\map\mapdisp\private中有 mstruct 的初始化文件 initmstruct.m,在这个文件中定义了 mstruct,如果需要传递参数,可以通过修改 mstruct的结构,他承载并传递一些其他自定义参数。为了实现“放大镜”式的等距离方位投影,需要rngz1作为内圆极距(公式中的z1),zoom_factor作为内外圆间的比例尺缩小系数(公式中的ge)。因此,在mstruct中定义如下参数并初始化。

(2)由于mstruct属于私有域,所以需要在axesm.m文件中添加自定义的setter方法,并在其setprop方法中调用setter方法设置mstruct。

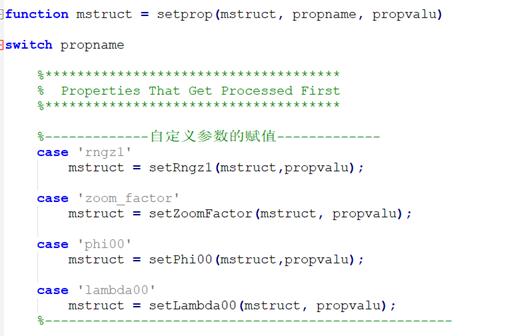
三、定义并注册地图投影
程序采用的是等距离方位投影制作具有“放大镜”效果的地图投影程序,因此可以直接在ortho投影的基础上进行复制,然后修改,自定义投影variable_ortho.m。
自定义投影的方法是在 E:\MATLAB2016a\toolbox\map\mapproj 路径添加自定义的 m 文件(variable_ortho.m)

然后在E:\MATLAB2016a\toolbox\map\mapproj路径下maplist.m 文件中,将自定义的variable_ortho投影进行注册,如下图所示:

这里同样要注意的是,有时mappingtoolbox工具箱莫名其妙找不到新注册的自定义投影,所以,如果遇到这种情况,大概就只得在已有投影(例如ortho.m)上进行修改了。
四、定义并注册地图投影
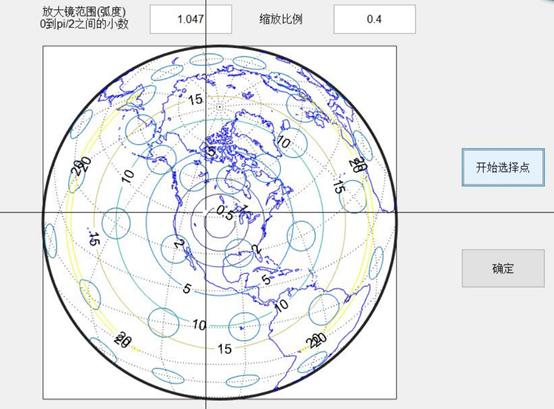
GUIDE是指matlab用于设计GUI (图形用户界面) 的工具环境。GUIDE做GUI的学习成本很低,具有直观和低门槛的优点,虽然用GUIDE做出来的程序可维护性很糟糕,但用于设计这样一个简单的具有位置拾取功能的投影程序绰绰有余(主要是简单),所以这里利用matlab的GUIDE来设计GUI程序。关于GUIDE的使用方法和GUI界面设计不是重点,这里就不过多阐述了,GUI程序写在variable_program.m和variable_program.fig文件,有兴趣的朋友可以参考。
其中“开始选择点”按钮,用于调用坐标拾取函数,获取当前鼠标点位置函数,“确定”按钮用于重绘“放大镜”等距离方位投影地图。为界面中的控件设置好回调函数之后即可使用。并可以通过放大镜范围设置参数z1和缩放比例ge。
坐标拾取可以采用 ginput 函数或 inputm 函数,前者是通过鼠标点击的位置获取当前的屏幕坐标(设备坐标 DP),使用后只需将获得坐标轴的屏幕坐标反算到逻辑坐标 LP,再利用地图投影的反算公式反算回地球表面经纬度,即可完成点的选择。而后者是通过将上述操作封装,直接利用鼠标点击的位置获取地球表面的经纬度坐标,可以说,inputm 函数拾取坐标非常简便,但又缺乏灵活性。
由于放大镜的原理,改变了黄圈外围(黄圈即为 z1 所在等高圈)的正算公式,导致投影反解公式在放大镜外围失效,从而无法 inputm 选点。可以考虑使用ginput来进行坐标拾取。
程序的部分代码如下(详见variable_program.m):
% 重置坐标轴,防止图像重叠
cla reset
% 确定时调用投影
landareas = shaperead('landareas.shp','UseGeoCoords',true);
[n,k]=size(landareas);
total = 1;
lon=zeros(1,20000);
lat=zeros(1,20000);
for j=1:n
[a,b]=size(landareas(j).Lon);
for m=1:b
lon(1,total) = [landareas(j).Lon(1,m)] ;
lat(1,total) = [landareas(j).Lat(1,m)] ;
total=total +1;
end
end
global phi00 lambda00;
%坐标轴采用自定义的variable_ortho投影类型
axesm ('variable_ortho', 'Frame', 'on', 'Grid', 'on','origin',[phi00 lambda00 0],'rngz1',[str2double(get(handles.edit1,'string'))],'zoom_factor',[str2double(get(handles.edit2,'string'))]);
geoshow(lat,lon);
tissot;
mdistort;
......省略部分代码......
%拾取经纬度坐标
[lat,lon]=inputm(1);
%判断经纬度坐标是否拾取成功
if ~isempty(lat) && ~isempty(lon)
phi00=lat;
lambda00=lon;
else
error(message('坐标反算失败'))
end
在该程序中,variable_program_OpeningFcn函数定义了程序启动时的初始化,pushbutton1_Callback函数定义了确定按钮单击事件的回调函数(改变投影图像),pushbutton3_Callback函数定义坐标拾取按钮单击事件的回调函数(用于拾取坐标),这三个函数是实现功能的主要函数。其中axesm函数是地图投影的核心,调用了自定义的variable_ortho投影
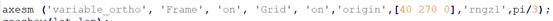
五、效果图
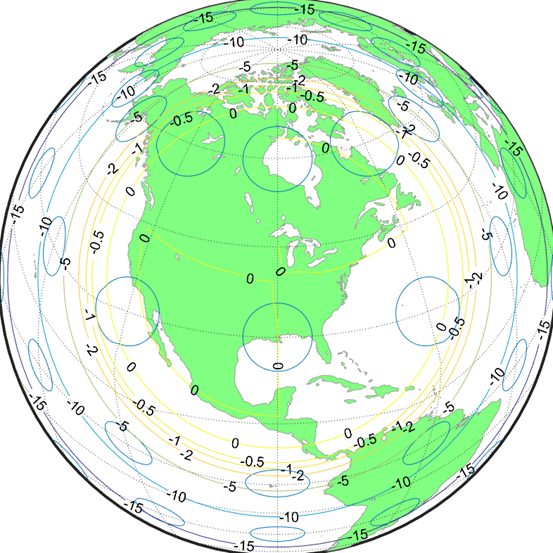
“放大镜”的效果取决于applyMagnifyingAzimuthalProjection.m中使用的公式,如果使用如下线性的等距离方位投影的公式,得到的效果如下图:
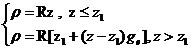
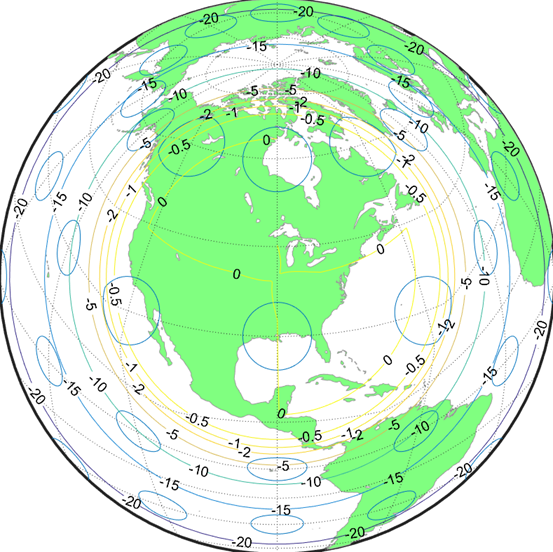
同理,如果使用非线性的从内圆到外圆过渡的等距离方位投影,例如0.7为指数的幂函数,就能实现“放大镜”式渐变方位投影: