主席树

主席树

权值树

在正常的树中，我们用下标来指元素(显然)
但，我们也可以用值指元素，显然的，不能开\(4\times10^9\)，于是，只能考虑动态建树

主席树

主席树，有黄嘉泰同志发明，因其缩写为时任主席的名字，故曰主席树

主席树是一种可持久优化的树，意思是，它保存历史信息（不忘初心），
或曰，主席树如何可持久化\

有线段树A,现在右子树增一结点，新线段树B如图

我们发现B的左子树未改变，因此对树略修改

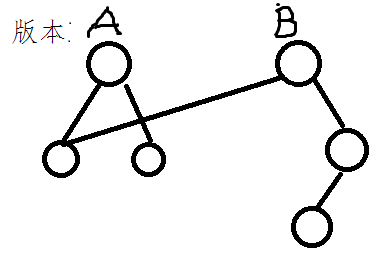
是的，我们让B的左子树指向A的左子树，这样，我们只要为右子树增开少量空间即可
让我们在C点继续开结点，画面越发诡异

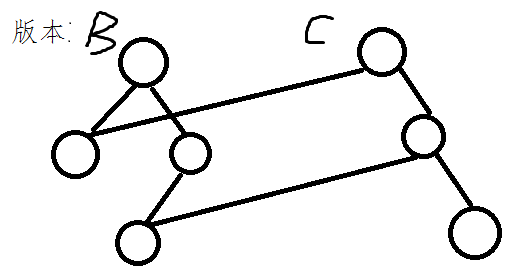
结论，增加结点增且仅增加根到此结点路径上的结点，总复杂度是\(\Omicron(\log10^9)\)

在加新节点时，不断比较与旧的差别，有就修改，不然就保持原样（连着原来的点）

以下是部分代码实现

#define lc(rt) t[rt].ls
#define rc(rt) t[rt].rs
#define sz(rt) t[rt].sz
void up(int rt)
{
    sz(rt) = sz(lc(rt)) + sz(rc(rt));
}
void ins(int &rt, int ls, int l, int r, int v)
//这里使用“引用”，使得下面对rt的修改会覆盖原本值
{
    t[rt = ++tot] = t[ls];
    if (l == r)
        sz(rt)++;
    else
    {
        if (v <= mid)
            ins(lc(rt), lc(ls), l, mid, v);
        else
            ins(rc(rt), rc(ls), mid + 1, r, v);
        up(rt);
    }
}

接下来，我们要面对的问题即是如何求第k小的值
我们把\([L,R]\)区间看做在树R与树L-1间新增的结点，首先比较左边新增的个数，若大于k，显然，要找的数在左边

int x = sz(lc(rt2)) - sz(lc(rt));
if (x >= k)
    return que(lc(rt), lc(rt2), l, mid, k);

不然就在右边

else
    return que(rc(rt), rc(rt2), mid + 1, r, k - x);

代码就是这样罢

int que(int rt,int ls, int l, int r, int k)
{
    if (l == r)
        return l;//权值树，l就是值
    int x = sz(lc(rt)) - sz(lc(ls));
    if (x >= k)
        return que(lc(ls), lc(rt), l, mid, k);
    else
        return que(rc(ls), rc(rt), mid + 1, r, k - x);
}

以下是全code

#include <bits/stdc++.h>
#define mid ((l + r) >> 1)
#define lc(rt) t[rt].ls
#define rc(rt) t[rt].rs
#define sz(rt) t[rt].sz
#define all 1, INF
using namespace std;
const int N = 5e5, M = N * 30, INF = 1e9;
struct node{int ls, rs, sz;} t[M];int n, m, tot, rt[N];
void up(int rt){sz(rt) = sz(lc(rt)) + sz(rc(rt));}
void ins(int &rt, int ls, int l, int r, int v)
//ls表上一个树
{
    t[rt = ++tot] = t[ls];
    if (l == r) sz(rt)++;
    else
    {
        if (v <= mid) ins(lc(rt), lc(ls), l, mid, v);
        else ins(rc(rt), rc(ls), mid + 1, r, v);
        up(rt);
    }
}
int que(int rt,int ls, int l, int r, int k)
//rt表L,rt2表R
{
    if (l == r) return l;//权值树，l就是值
    int x = sz(lc(rt)) - sz(lc(ls));
    if (x >= k)return que(lc(rt), lc(ls), l, mid, k);
    else return que(rc(rt), rc(ls), mid + 1, r, k - x);
}
int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1, x; i <= n; i++) scanf("%d", &x), ins(rt[i], rt[i - 1], all, x);
    for (int i = 1, a, b, c; i <= m; i++) 
        scanf("%d %d %d", &a, &b, &c), printf("%d\n", que(rt[b], rt[a - 1], all, c));
    return 0;
}