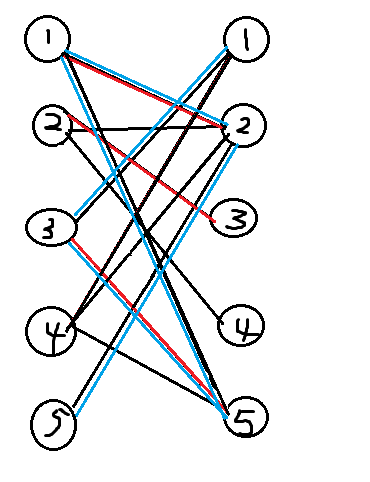
二分图匹配(匈牙利算法和KM算法)
二分图匹配
对于一个二分图,其匹配是一个边的集合,每条边不应用重复的点
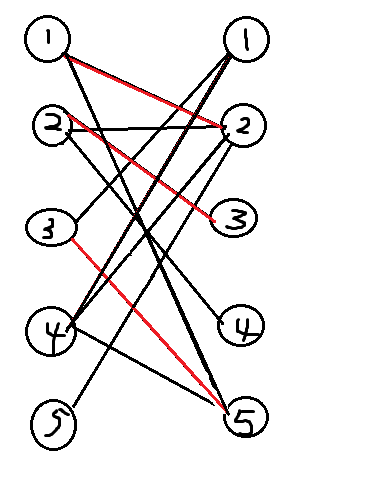
它有一个匹配,为图中红色线段
但这个匹配不是(边数)最大的,因此不是最大匹配
匈牙利算法
匈牙利算法用增广路径寻找最大匹配
增广路径
增光路经以一条非匹配边开始和结束,中间交替出现非匹配边和匹配边
将增广路径上的边取反,匹配边变未匹配,未匹配变匹配
发现多了一条匹配边,这是增广路的一个性质
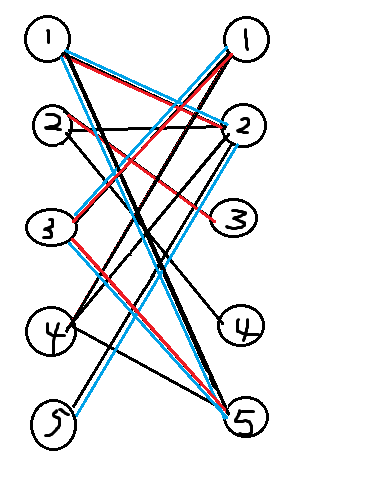
匈牙利算法用增广路的性质,匹配边数不断加一,直到找不到增广路\
bool dfs(int x)
{
//返回1表示有增广路
for(auto y : q[x])
{
if(!vis[y])//没有访问过
{
vis[y]=1;
if(!cet[y]||dfs(cet[y]))
//如果y没有与任何点匹配,或y已经匹配,但往下找有增广路
{
cet[y]=x;//重新连接
return 1;
}
}
}
return 0;
}
int hungary()
{
int ans = 0;
for (int i = 1; i <= n; i++)
{
memset(vis, 0, sizeof(vis));
if (dfs(i))//有增广路
ans++;
}
return ans;
}
KM算法
匈牙利算法在面对最佳匹配时不尽人意
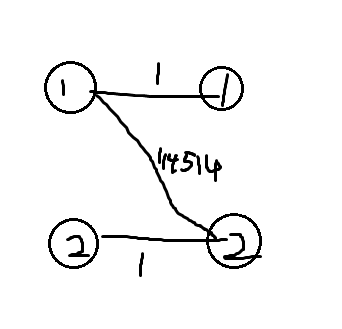
\(1+1>114514?\)
有没有什么好办法呢?
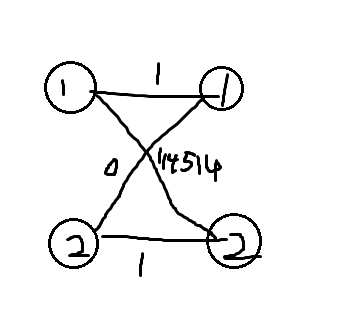
加一条\(有关紧要\)的边,总之就是使图每两点都有边
此时\(1+1<0+114514\),我们把\(0+114514\)这样的,又是最大匹配,权值又最大的匹配称为\(最大权匹配\)
\(KM算法\)求解最大权匹配,显然,如果不加有关紧要的边,它求的就是最大匹配
\(KM算法\)设置顶标,顶标是此点所连的最大边的权值,特别地,另一部分的顶标为0
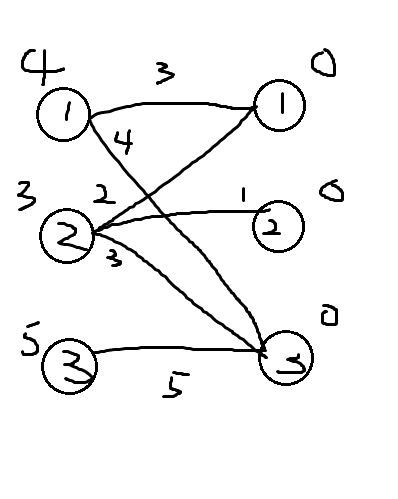
相等子图,由顶标和为其边值的两点的边组成
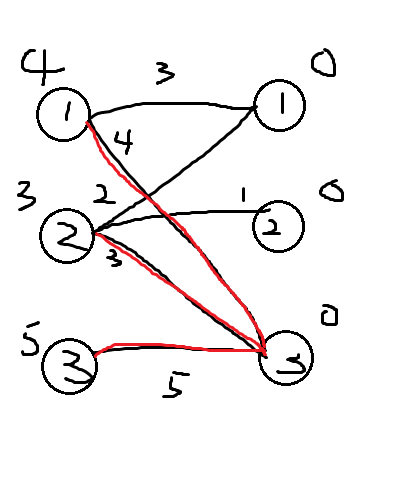
现在相等子图中找一条增广路径,显然它是\(1-3\)这一条边
取反,再找一次,却没有增广路径了
对于这种情况,我们需要扩大相等子图
在子图中,左部减少\(d\),右部增加\(d\)
对于边
- 对于两端都在相等子图中的,顶标和不变,仍位于子图中
- 对于两端都不在相等子图中的,顶标和不变,仍不在子图中
- 对于左端顶点在相等子图中的,顶标和减小,可能成为
同志相等子图中的边 - 对于右端顶点在相等子图中的,顶标和减小,仍不在子图中
所以,如何把\(d\)值控制的柔韧有余,就可以防止出现顶标和小于边权的情况
我们注意到对于左端顶点在相等子图中的,顶标和减小,可能加入相等子图
所以对于所有不完整增广路径中的边的左端点,都应该让左部的顶标减少\(d\)
\(d\)的值是多少呢,显然,只有上面所说的边的顶标和,与其边之差中的最小差,显然就是最好的\(d\)
定理:相等子图中,如果存在整个图的完备匹配,则其边权和为所有顶点顶标和且此匹配即为最佳匹配
原因:因为我们减的是最小的\(d\),进入的边肯定就是最大的,当出现完备匹配时,所有点所连的最大边,都已经在相等子图中了,显然,这就是最佳匹配
int n, w[N][N];//边权
int cet[N], mn;//连接;求d的最小值
int vx[N], vy[N], wx[N], wy[N];//标记数组和顶标数组
bool dfs(int x)//找增广路径
{
vx[x] = 1;//标记位于不完整增广路径内
for (int i = 1; i <= n; i++)
{
if (vy[i])
continue;
int t = wx[x] + wy[i] - w[x][i];//可能的d
if (!t)//t==0时,位于相等子图内
{
vy[i] = 1;//标记位于不完整增广路径内
if ((!cet[i] || dfs(cet[i]))&&(cet[i]=x))
return 1;
}
else
mn = min(mn, t);//求最小的d值
}
return 0;
}
int km()
{
for (int i = 1; i <= n; i++)
{
cet[i] = wy[i] = 0, wx[i] = -I;
for (int j = 1; j <= n; j++)
wx[i] = max(wx[i], w[i][j]);//左部为其所连之最大边
}//初始化
for (int i = 1; i <= n; i++)
{
for (;;)
{
mn = I;
#define init(x) memset(x, 0, sizeof(x))
init(vx), init(vy);
if (dfs(i))//能找到增广路
break;
for (int j = 1; j <= n; j++)
{
if (vx[j])
wx[j] -= mn;//左部的顶标减去d
if (vy[j])
wy[j] += mn;//右部的顶标加上d
}
}
}
int ans = 0;
for (int i = 1; i <= n; i++)
ans += w[cet[i]][i];//计算最佳匹配的答案
return ans;
}
此外的
相等子图还有其他性质,
- 在任意时刻,相等子图上的最大权匹配一定小于等于相等子图的顶标和
证:显然地,可能有的点在相等子图内但却没有在最大权匹配中,你总不能把它们忽略不计吧 - 在任意时刻,相等子图的顶标和即为所有顶点的顶标和
证:仔细观察,左边的都进子图了,右边没进去的顶标都是0,不影响 - 扩充相等子图后,相等子图的顶标和将会减小
证:因为,一开始是,左边的每一个点都进入相等子图,但右边却不可能不然这题就不用做了
当我们给左边的顶标做减法时,减的值多余给右边加的值,顶标和自然会减少