『浅谈』manacher/马拉车/祥子算法

『浅谈』manacher算法

简介

作为一种求回文子串的算法,manacher几乎总是能在O(n)的时间求出

在有些时候manacher需要朴素算法,请先复习朴素算法
即

该算法通过下述方式工作：对每个中心位置 ，

在比较一对对应字符后，只要可能，该算法便尝试将答案加1。----- oi-wiki

正文

1. 首先为了避免奇偶要单独处理的情况,可以考虑在字符中间加入分割符使字符串长度固定为偶数
   1. 如abc变成@#a#b#c# (@是为了方便判断越界)
2. 变量铺垫
   • s表转换后(加入分割符)的字符串
   • len[i]表以i为中心点的回文串中,i到右(或左)边界的长度
   • l表上一次取得的最大的回文串左边界
   • r表上一次取得的最大的回文串右边界
   • mid上一次的终点
   • j表i相对于mid的对应点(已经求出的)
     若存在j,则 j=mid-(i-mid)=2*mid-i
   • i表一回文串的中点
   • mx表最大的长度
3. then

for(i 1~s长度  (遍历))    枚举中点
	if(i在以mid为中心的回文串内)
		if(以i为中点的回文串的右端在以mid为中心的内部)
			如下图1
			因为 j是i相对于mid的对称点，回文串倒着显然还对称
			所以len[i]大于或等于len[j]
			先让len[i]=len[j],后面再用朴素算法把大于的求出来
			所以
			for(len[i]=len[j];s[i-len[i]]==s[i+len[i]];len[i]++);
		else
			如下图2
			此时 以i为中点的回文串只确定了(r-i)
			所以len[i]大于或等于r-i
			所以再用朴素算法求剩下的
			for(len[i]=r-i;s[i-len[i]]==s[i+len[i]];len[i]++);
	else
		此时说明以i为中点的回文串没有一点是确定的
		所以len[i]大于或等于1(一个字符也是回文串)
		直接朴素算法
		for(len[i]=1;s[i-len[i]]==s[i+len[i]];len[i]++);
	if(以i为中点的回文串的右边界大于上一次的r)
		更新r,mid
		mx=max(mx,len[i]);

最后答案=(mx-1)/2*2=mx-1

-1删除末尾的'#'
/2把#删掉
*2是把回文串的另一半加上

图1

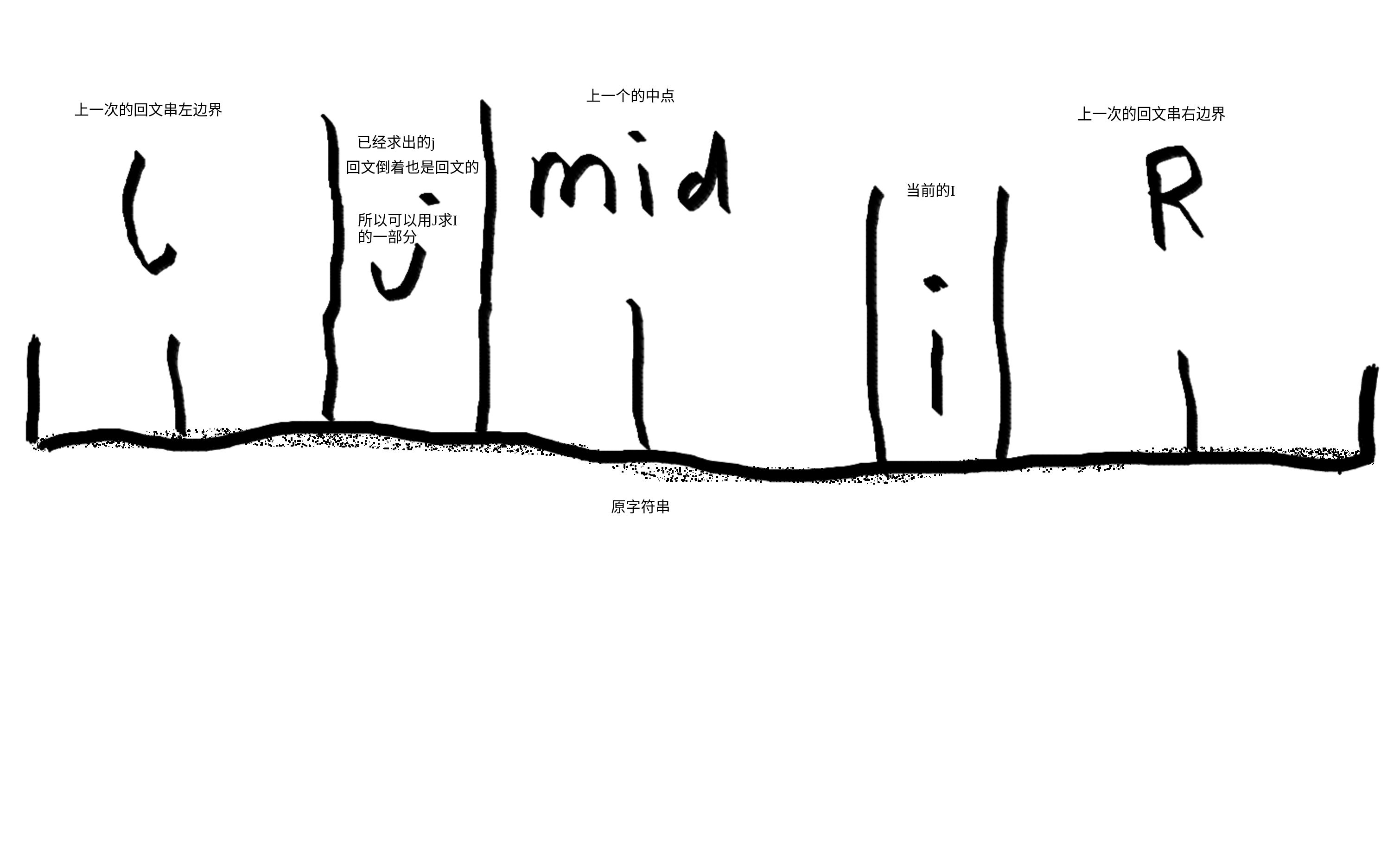
图2

CODE

//By CPP17
int manacher(string s)
{
	int len[s.size() << 1], mid, r = 0，mx = -1；
	for (int i = 0; i < (int)s.size(); i++)
	{
		if(i<r)//i在以mid为中心的回文串内
		{
			int j = mid - i + mid;
			if (len[j]<=r-i)//以i为中点的回文串的右端在以mid为中心的内部
				for(len[i]=len[j];s[i-len[i]]==s[i+len[i]];len[i]++);
			else
				for(len[i]=r-i;s[i-len[i]]==s[i+len[i]];len[i]++);
		}
		else
			for(len[i]=1;s[i-len[i]]==s[i+len[i]];len[i]++);
		if(len[i]+i>r)//更新
		{
			r=len[i]+i;
			mid=i;
			mx=max(mx,len[i]);
		}
	}
	return mx - 1;
}