夜空深处,闪亮的星星以星群的形式出现在人们眼中,形态万千。
一个星群是指一组非空的在水平,垂直或对角线方向相邻的星星的集合。
一个星群不能是一个更大星群的一部分。
星群可能是相似的。
如果两个星群的形状、包含星星的数目相同,那么无论它们的朝向如何,都认为它们是相似的。
通常星群可能有 88 种朝向,如下图所示:
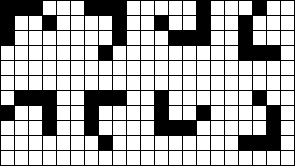
现在,我们用一个二维 0101 矩阵来表示夜空,如果一个位置上的数字是 11,那么说明这个位置上有一个星星,否则这个位置上的数字应该是 00。
给定一个夜空二维矩阵,请你将其中的所有星群用小写字母进行标记,标记时相似星群用同一字母,不相似星群用不同字母。
标注星群就是指将星群中所有的 11 替换为小写字母。
输入格式
第一行包含一个整数 WW,表示矩阵宽度。
第二行包含一个整数 HH,表示矩阵高度。
接下来 HH 行,每行包含一个长度为 WW 的 0101 序列,用来描述整个夜空矩阵。
输出格式
输出标记完所有星群后的二维矩阵。
用小写字母标记星群的方法很多,我们将整个输出读取为一个字符串,能够使得这个字符串字典序最小的标记方式,就是我们想要的标记方式。
输出这个标记方式标出的最终二维矩阵。
数据范围
0≤W,H≤1000≤W,H≤100,
0≤0≤ 星群数量 ≤500≤500,
0≤0≤ 不相似星群数量 ≤26≤26,
1≤1≤ 星群中星星的数量 ≤160≤160
输入样例:
23
15
10001000000000010000000
01111100011111000101101
01000000010001000111111
00000000010101000101111
00000111010001000000000
00001001011111000000000
10000001000000000000000
00101000000111110010000
00001000000100010011111
00000001110101010100010
00000100110100010000000
00010001110111110000000
00100001110000000100000
00001000100001000100101
00000001110001000111000
输出样例:
a000a0000000000b0000000
0aaaaa000ccccc000d0dd0d
0a0000000c000c000dddddd
000000000c0b0c000d0dddd
00000eee0c000c000000000
0000e00e0ccccc000000000
b000000e000000000000000
00b0f000000ccccc00a0000
0000f000000c000c00aaaaa
0000000ddd0c0b0c0a000a0
00000b00dd0c000c0000000
000g000ddd0ccccc0000000
00g0000ddd0000000e00000
0000b000d0000f000e00e0b
0000000ddd000f000eee000
样例解释
样例对应的星空图如下:

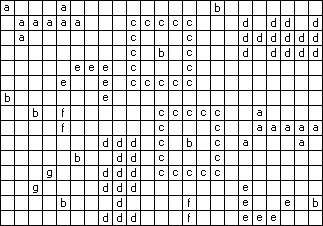
答案对应的标记后星空图如下:

//不同形状的区分利用哈希来完成: //求连通块中任意2点之间的直线距离之和 //注意不能不开方直接用用平方数,结果和开方不同 //比如 1111 他们不开方距离为1+4+9+1+1+4+1=20,开方:也是20 //而 1 // 11 // 1 他们不开方距离也是(2+2+4)*4/2+1+1+1+1=20;开方(1.414+1.414+2)*2+4 //使用哈希函数,如果一个不保险可以使用多个哈希函数 //两线之间距离哈希有出错的情况,概率很低 //本题细节比较多,逻辑有点复杂 //拓展字符串哈希841 ,很多情况下可以替换KMP //常见做法、写法、常规算法需要积累 //积累代码片段 //非递归并不是比递归快,因为系统有优化 //acm偏向速度 //noip偏向思维 #include<iostream> #include<cmath> #include<cstring> #include<cstdio> using namespace std; const int dx[10]={1,0,-1,0,1,-1,-1,1}; const int dy[10]={0,1,0,-1,1,-1,1,-1}; int w,h,cnt; char ch; char a[110][110]; int b[10100][3]; double c[300]={0};//注意数据类型 double cal(){ double sum=0; /* cout<<cnt<<":"; for(int i=1;i<=cnt;i++) cout<<b[i][0]<<" "<<b[i][1]<<endl;*/ for(int i=1;i<cnt;i++) for(int j=i+1;j<=cnt;j++) sum+=sqrt(double(b[i][0]-b[j][0])*(b[i][0]-b[j][0])+(b[i][1]-b[j][1])*(b[i][1]-b[j][1])); // printf("%.8lf \n",sum); return sum; } void solve(){ double sum=cal(); int p=0; for(int i='a';i<ch;i++){ if(abs(c[i]-sum)<=1e-8){//注意取绝对值 p=i; break; } } if(p){ for(int i=1;i<=cnt;i++) a[b[i][0]][b[i][1]]=p; } else { for(int i=1;i<=cnt;i++) a[b[i][0]][b[i][1]]=ch; c[ch]=sum; ch++; } } void dfs(int x,int y){ a[x][y]='0';//注意标志 b[++cnt][0]=x;b[cnt][1]=y; for(int i=0;i<=7;i++){ int xx=x+dx[i],yy=y+dy[i]; if(xx>=1&&xx<=h&&yy>=0&&yy<w&&a[xx][yy]=='1'){ //a[xx][yy]='0';//防止重复访问 dfs(xx,yy); } } } int main(){ cin>>w>>h; for(int i=1;i<=h;i++) cin>>a[i]; ch='a'; for(int i=1;i<=h;i++) for(int j=0;j<w;j++){ cnt=0; if(a[i][j]=='1'){ memset(b,0,sizeof(b)); // a[i][j]='0';//注意标志 dfs(i,j); solve(); } } for(int i=1;i<=h;i++) cout<<a[i]<<endl; return 0; }




