随机游走问题
随机游走问题
随机游走问题:在一个图中,有一个棋子。它初始在某一个点上,然后开始移动。当它在\(u\)点时,可以移动到相邻的\(v\)点(相邻指两点之间存在一条边),它的概率是\(P_{u,v}\),而且\(\sum_{v,v与u相邻},P_{u,v}=1\)。那么我想知道从一个点出发,第一次到达另一个点平均要走几步?从一个点出发,走了有限步数,那么它目前处于某一个点的概率是多少?从一个点出发,走的步数趋近于无限,那么它目前处于某一个点的概率是多少?这些都是随机游走关心的问题。
树上随机游走
给定一棵树,还有\(q\)组询问,每组询问给出一个起点\(S\),一个终点\(F\),问从\(S\)出发,期望走几步恰好到达\(F\)。其中,树是一个无向图,如果一个点\(u\)的度数为\(d[u]\),那么任意与\(u\)相邻的\(v\),\(P_{u,v}=\frac{1}{d[u]}\)。
首先,处理这个问题的时候要知道期望距离的一个性质
性质:\(d(a,b)+d(b,c)=d(a,c)\),这里的\(d(a,b)\)表示从\(a\)出发,恰好走到\(b\)时,期望走的步数。
证明:
假设\(a,c\)不相邻,在从\(a\)到\(c\)的简单路径上存在一点\(b\)(简单路径指路径上的点不重复)
根据树的性质,两点之间只能存在一条简单的路径
所以想从\(a\)出发到达\(c\),必须经过\(b\)
那么把从\(a\)出发到\(c\)结束的顶点编号记下来,可以看成是
\(v_1,v_2,...,v_k\)
其中\(v_1=a,v_k=c\),\(\exists t,v_t=b\)
而且\(\forall t,v_t=c\to t=k\)
那么我们不妨设满足\(\exists t,v_t=b\),\(t\)的最小值为\(m\)
\(v_1,v_2,...,v_m\)即从\(a\)出发,第一次到达\(b\)的一条路径
\(Ex(m-1)=d(a,b)\)
\(v_m,v_{m+1},...,v_k\)即从\(b\)出发,第一次到达\(c\)的一条路径
\(Ex(k-m)=d(b,c)\)
\(\because v_1,v_2,...,v_m\)序列与\(v_m,v_{m+1},...,v_k\)无关(不考虑\(v_m\)的话)
\(\therefore m-1\)的分布与\(k-m\)的分布无关
\(Ex(k-1)=Ex(m-1)+Ex(k-m)=d(a,b)+d(b,c)\)
\(\because\)按照定义 \(d(a,c)=Ex(k-1)\)
\(\therefore d(a,b)+d(b,c)=d(a,c)\)
这个性质告诉我们,两个相邻点之间的期望步数可以看成两个点之间的边权。
从\(S\)点到\(F\)点,需要计算\(S,F\)的简单路径的边权和。
给一棵带边权的树,那么可以在\(O(nlogn)\)的预处理后,使用\(LCA\)与连续和的方法在\(O(log\,n)\)的时间内求出\(S,F\)的期望距离。\(LCA\)算法本文暂且不讲,读者可以自行搜索,这里先讲边权如何处理。
边权的计算方法
本题的情景虽然是树,但是这里要当成有向图处理。注意\(d(a,b)\ne d(b,a)\),比如树的点数为3
边为\((1,2),(2,3)\),那么\(d(1,2)=1\),\(d(2,1)=3\),是不相等的。
比如我们要求\(d(u,v)\),\(u\)是起点,\(v\)是终点,而且\(u,v\)相邻
设\(d[u]\)为\(u\)的度数
那么有2种情况
1.\(d[u]=1\),即\(u\)唯一的相邻点就是\(v\),那么显然从\(u\)出发走一步就是\(v\)
\(\therefore d(u,v)=1\)
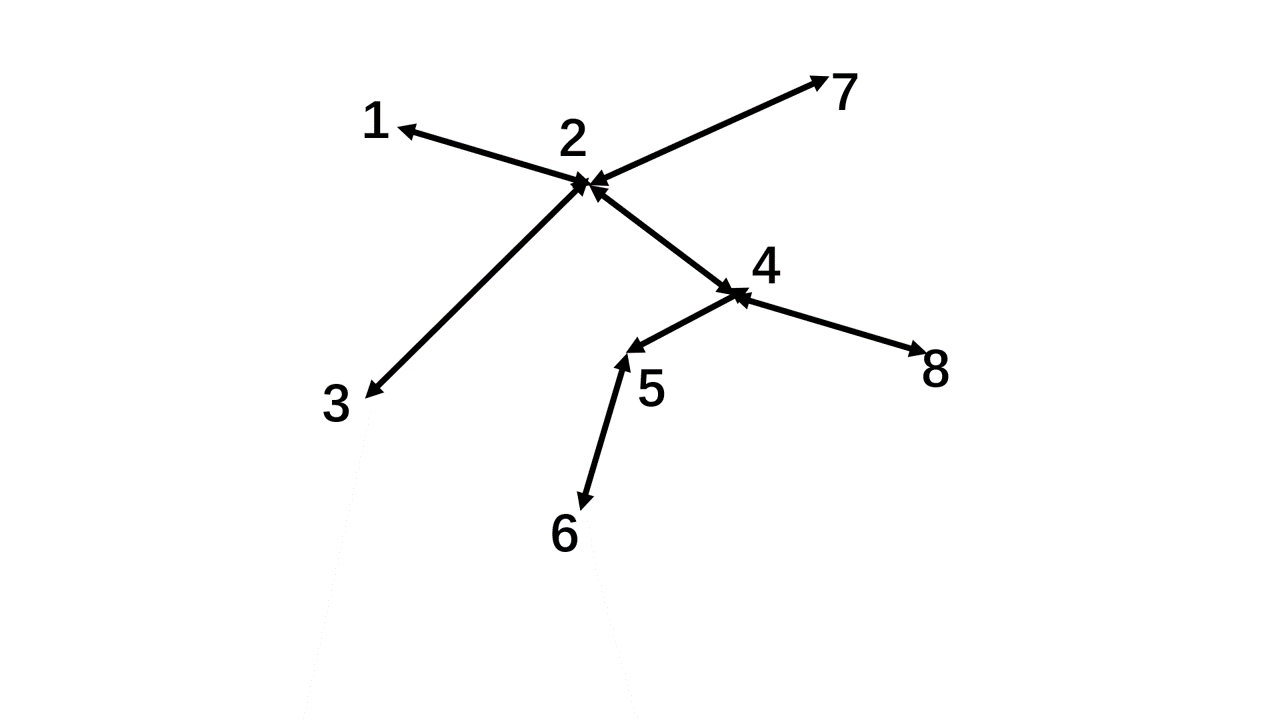
2.\(d[u]>1\),那么从\(u\)点出发有\(d[u]\)种等可能选择
其中,到\(v\)的可能性是\(\frac{1}{d[u]}\)
到其它点的可能性之和是\(\frac{d[u]-1}{d[u]}\)
从\(u\)节点出发,最终到了\(v\)节点,我们假设在这个路径中,从\(u\)走到\(v\)之外的相邻节点恰好\(k\)次。
说明概率\(\frac{d[u]-1}{d[u]}\)的事件连续发生了\(k\)次,之后概率\(\frac{1}{d[u]}\)的事件发生了一次,
记为\(P(sub_k)=\frac{1}{d[u]}(\frac{d[u]-1}{d[u]})^k\)
然后在事件\(sub_k\)下,从\(u\)走到\(v\)之外的相邻节点恰好\(k\)次,每次选择哪一个节点都是随机的,
每一次的条件概率为\(\frac{1}{d[u]-1}\)。
那么设某一次,从\(u\)走到\(v\)之外的相邻节点\(y\),需要1步,然后再从\(y\)返回\(u\),又需要期望\(d(y,u)\)步
其中,\(y\)完全是随机的。
那么这一次,从\(u\)走到\(v\)之外的相邻节点\(y\),再回到\(u\),需要的期望步数为
\(\sum_{u,y相邻,y\ne v}\frac{1}{d[u]-1}(1+d(y,u))\)。
这种事件连续发生了\(k\)次,所以总的期望步数为\(k\sum_{u,y相邻,y\ne v}\frac{1}{d[u]-1}(1+d(y,u))\)
由于最后一步一定是从 \(u\) 走到 \(v\),再加\(1\)
\(\therefore d(u,v)=1+\sum_{k=0}^{\infty} P(sub_k)k\sum_{u,y相邻,y\ne v}\frac{1}{d[u]-1}(1+d(y,u))\)
\(=1+(\sum_{k=0}^{\infty} \frac{kP(sub_k)}{d[u]-1})\times \sum_{u,y相邻,y\ne v}(1+d(y,u))\)
其中\((\sum_{k=0}^{\infty} \frac{kP(sub_k)}{d[u]-1})=\frac{1}{d[u]}\frac{1}{d[u]-1}\sum_{k=0}^{\infty} k(\frac{d[u]-1}{d[u]})^k\)
其中,\(\sum_{k=0}^{\infty} k(\frac{d[u]-1}{d[u]})^k\)应用错位相减法,
求得\(\sum_{k=0}^{\infty} k(\frac{d[u]-1}{d[u]})^k=(d[u]-1)(d[u])\)
\(\therefore (\sum_{k=0}^{\infty} \frac{kP(sub_k)}{d[u]-1})=1\)
\(\therefore d(u,v)=1+\sum_{u,y相邻,y\ne v}(1+d(y,u))\)
综上
\(d(u,v)=1+\sum_{u,y相邻,y\ne v}(1+d(y,u))\)
如何编程计算?
对于一棵树,我们可以令点\(1\)为根,形成一棵有根树(这才有深度和父子关系)。设\(S,F\)的最近公共祖先为\(M\),从\(S\)到\(F\)的简单路径,可以看成一条从\(S\)到\(M\)的上行路径(上行即深度越来越浅,往树根方向走),与一条从\(M\)到\(F\)的下行路径(上行即深度越来越深,往树根反方向走)。
设\(now\)为某个节点的编号,\(fa[now]\) 为\(now\)的父节点,设\(up[now]\)为从\(d(now,fa[now])\),设\(down[now]=d(fa[now],now)\)。
\(up[now]\)的计算
\(now\ne 1\)
1.\(d[now]>1\),即\(now\)不是叶节点
根据\(d(u,v)=1+\sum_{u,y相邻,y\ne v}(1+d(y,u))\)
\(up[now]=d(now,fa[now])=1+\sum_{now,y相邻,y\ne fa[now]}(1+d(y,now))\)
由于满足\(now,y相邻,y\ne fa[now]\)的\(y\)都是\(now\)的子节点
上式\(=1+\sum_{fa[y]=now}(1+up[y])\)
2.\(d[now]=1\),即\(now\)是叶节点
那么根据\(d(u,v)=1\)
\(up[now]=d(now,fa[now])=1\)
综上,
\(up[now]=1+\sum_{fa[y]=now}(1+up[y])\)
这是一个递归的定义式,可以递归求解。
我们不妨设\(sum\_up[now]=\sum_{fa[y]=now}(1+up[y])\)
\(up[now]=1+sum\_up[now],now\ne 1\)
\(down[now]\)的计算
\(now\ne 1\)
1.\(fa[now]\ne 1\),即\(now\)不是树根的儿子
根据\(d(u,v)=1+\sum_{u,y相邻,y\ne v}(1+d(y,u))\)
\(down[now]=d(fa[now],now)=1+\sum_{fa[now],y相邻,y\ne now}(1+d(y,fa[now]))\)
\(=1+\sum_{fa[now],y相邻}(1+d(y,fa[now]))-d(now,fa[now])-1\)
\(=\sum_{fa[now],y相邻,y\ne fa[fa[now]]}(1+d(y,fa[now]))+1+d(fa[fa[now]],fa[now])-d(now,fa[now])\)
由于满足\(fa[now],y相邻,y\ne fa[fa[now]]\)的\(y\)都是\(fa[now]\)的儿子
\(down[now]=\sum_{fa[y]=fa[now]}(1+d(y,fa[now]))+d(fa[fa[now]],fa[now])-d(now,fa[now])+1\)
\(=\sum_{fa[y]=fa[now]}(1+up[y])+down[fa[now]]-up[fa[now]]+1\)
\(=sum\_up[fa[now]]+down[fa[now]]-up[fa[now]]+1\)
2.\(fa[now]=1\),即\(now\)是树根的儿子
\(d(u,v)=1+\sum_{u,y相邻,y\ne v}(1+d(y,u))\)
\(down[now]=d(fa[now],now)=1+\sum_{fa[now],y相邻,y\ne now}(1+d(y,fa[now]))\)
\(=1+\sum_{fa[now],y相邻}(1+d(y,fa[now]))-d(now,fa[now])-1\)
\(\because fa[now]=1\),是根节点
\(\therefore 满足fa[now],y相邻\)的\(y\)都是\(fa[now]\)的儿子
\(\therefore down[now]=1+\sum_{fa[y]=fa[now]}(1+d(y,fa[now]))-d(now,fa[now])-1\)
\(=\sum_{fa[y]=fa[now]}(1+up[y])-up[now]\)
\(=sum\_up[fa[now]]-up[now]\)
综上,
最后再把这两个结论放在一起
\(up[now]=1+sum\_up[now],now\ne 1\)
其中\(sum\_up[now]=\sum_{fa[y]=now}(1+up[y])\)
我们先利用一个\(dfs\)计算\(up[now]\)和\(sum\_up[now]\),再利用另一个\(dfs\)计算\(down[now]\)
这样我们就把任意两个相邻点之间的期望步数算出来了,由递归定义可知,它们都是正整数,不用考虑分数的情况。
求任意两点的期望步数
现在这就是一个图论问题了,因为边权都已经求出来了(注意边权是分向树根方向和向树叶方向的),现在需要求任意两点之间的距离。提示:这个需要用到\(LCA\)
最后贴出代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
int read()
{
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while( isdigit(c)){x=x*10+c-'0';c=getchar();}
return x*f;
}
ll mod=1000000007;
const int maxn=1e5+10;
ll d[maxn];//度数
struct edge
{
int y,next;
}map[maxn*2];
int head[maxn];
ll up[maxn],down[maxn];
ll sum_up[maxn];
void add(int num,int x,int y)
{
map[num].y=y;
map[num].next=head[x];
head[x]=num;
d[x]++;
}
void dfs_up(int now,int fa)
{
ll ans=0;
for(int k=head[now];k!=-1;k=map[k].next)
{
int y=map[k].y;
if(y==fa)continue;
dfs_up(y,now);
ans=(ans+1+up[y])%mod;
}
sum_up[now]=ans;
if(d[now]>1)//不是叶节点
{
ans=ans;//数学公式
}
ans=(ans+1)%mod;
up[now]=ans;
if(now==1)
{
up[now]=0;
}
}
void dfs_down(int now,int fa)//从fa走到now
{
if(now==1)
{
down[now]=1;
}
else if(fa==1)
{
down[now]=(sum_up[fa]-up[now]+mod)%mod;
}
else
{
down[now]=(sum_up[fa]-up[now]+down[fa]+1+mod)%mod;
}
for(int k=head[now];k!=-1;k=map[k].next)
{
int y=map[k].y;
if(y==fa)continue;
dfs_down(y,now);
}
}
ll pre_up[maxn],pre_down[maxn];
int deep[maxn],ance[maxn][18];
void dfs(int now,int fa)
{
for(int k=head[now];k!=-1;k=map[k].next)
{
int y=map[k].y;
if(y==fa)continue;
ance[y][0]=now;
deep[y]=deep[now]+1;
pre_up[y]=(up[y]+pre_up[now])%mod;
pre_down[y]=(down[y]+pre_down[now])%mod;
for(int temp=2,i=0;deep[y]>temp;i++,temp*=2)//temp=2^(i+1)
{
ance[y][i+1]=ance[ance[y][i]][i];
}
dfs(y,now);
}
}
int LCA(int x,int y)
{
if(deep[x]>deep[y])swap(x,y);
//x一定比y浅(或同深度)
int del=deep[y]-deep[x];
for(int i=0;del>0;i++,del/=2)
{
if(del%2==1)
{
y=ance[y][i];
}
}
//x,y同深度
int len=0;
int dep=deep[x];
while(dep)
{
dep/=2;
len++;
}
for(int i=len;i>0;i--)
{
if(ance[x][i]==ance[y][i]&&ance[x][i-1]!=ance[y][i-1])
{
x=ance[x][i-1];
y=ance[y][i-1];
}
}
if(x!=y)return ance[x][0];
else return x;
}
int main()
{
memset(head,-1,sizeof(head));
int n=read(),q=read();
for(int i=1;i<n;i++)
{
int x=read(),y=read();
add(i*2-1,x,y);
add(i*2,y,x);
}
dfs_up(1,-1);
dfs_down(1,-1);
deep[1]=1;
dfs(1,-1);
while(q--)
{
int x=read(),y=read();
int lca=LCA(x,y);
ll ans=(pre_up[x]-pre_up[lca]+pre_down[y]-pre_down[lca]+2*mod)%mod;
printf("%lld\n",ans);
}
}
无向图的随机游走问题
设一个无向图,有一个棋子从某点出发,随机游走,问它在运动几步后处于某个点的概率
设图的联通性矩阵为\(A\)
\(A_{ij}\)表示第\(i,j\)两点是否相邻
比如这个矩阵
即下图
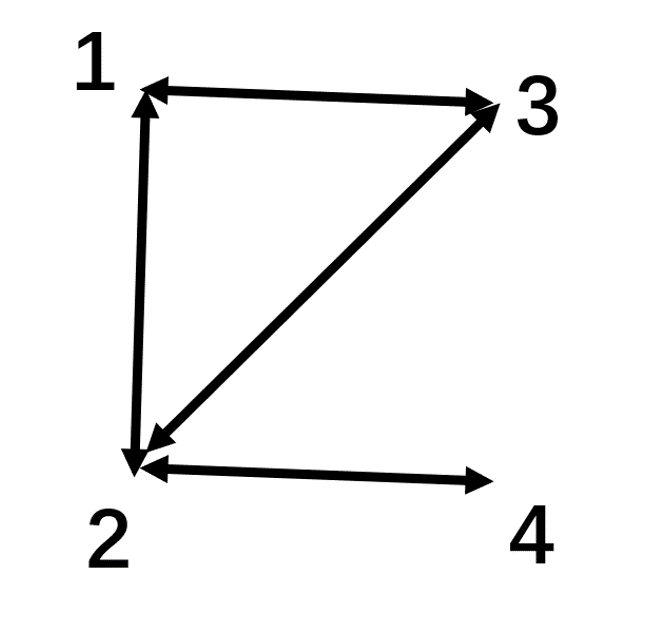
还有度数矩阵\(B\)
它是一个对角矩阵
\(B_{ii}=d[i]\)
该图的度数矩阵\(B\)为
设当前的状态向量\(p\)
\(p_{i1}=P(i)\),即在\(i\)点处的概率
那么走到下一步后
\(p^{'}=AB^{-1}p\)
这一步是很抽象的,希望读者自己推理
由这一点得出的另一个非常有意思的结论:
无论初始状态\(p\)如何
当走的步数趋近于无穷大时,\(p\)收敛于\(p_{i1}=\frac{d[i]}{\sum_{i=1}^{n}d[i]}\)
即一个棋子在随机游走了无穷步后处于一个点的概率和这个点的度数成正比


 浙公网安备 33010602011771号
浙公网安备 33010602011771号