数据归一化:将所有数据映射到同一尺度
常用方式:最值归一化 均值方差归一化
最值归一化(normalization)
把所有数据都映射到0-1之间
适用范围: 适用于特征数组元素有明显的分布边界的情况(如学生成绩,最高100, 最低0),但是会受到outlier(异常值)的影响
![]()
均值方差归一化
把所有数据都映射到均值为0,方差为1的分布中
适用范围:数据分布没有明显边界,有可能存在异常值的情况 (均值方差归一化对于有明显边界的分布也比较友好,所以一般都推荐均值方差归一化)
![]()
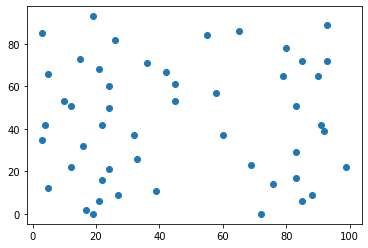
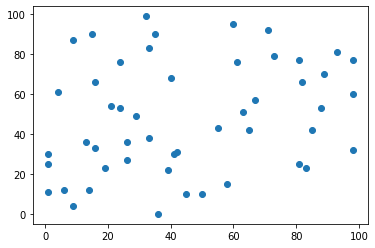
手动对特征数组进行最值归一化
# 生成一个(50,2)的随机数组,使用matplotlib绘制散点图
X = np.random.randint(0, 100, (50, 2))
X = np.array(X, dtype=float)
X
plt.scatter(X[:,0], X[:,1])
plt.show()
![]()
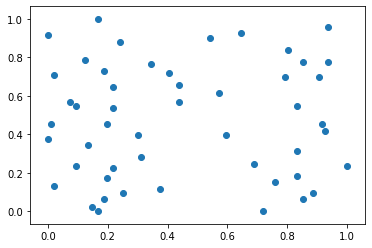
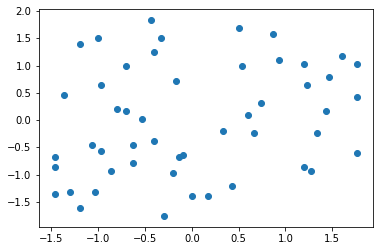
# 进行最值归一化
X[:,0] = (X[:,0] - np.min(X[:,0])) / (np.max(X[:,0]) - np.min(X[:,0]))
X[:,1] = (X[:,1] - np.min(X[:,1])) / (np.max(X[:,1]) - np.min(X[:,1]))
plt.scatter(X[:,0], X[:, 1])
plt.show()
![]()
手动对特征数组进行均值方差归一化
# 生成一个(50,2)的随机数组,使用matplotlib绘制散点图
X = np.random.randint(0, 100, (50, 2))
X = np.array(X, dtype=float)
X
plt.scatter(X[:,0], X[:,1])
plt.show()
![]()
# 进行均值方差归一化
X[:, 0] = (X[:,0] - np.mean(X[:,0])) / np.std(X[:, 0])
X[:, 1] = (X[:,1] - np.mean(X[:,1])) / np.std(X[:, 1])
plt.scatter(X[:, 0], X[:, 1])
plt.show()
![]()
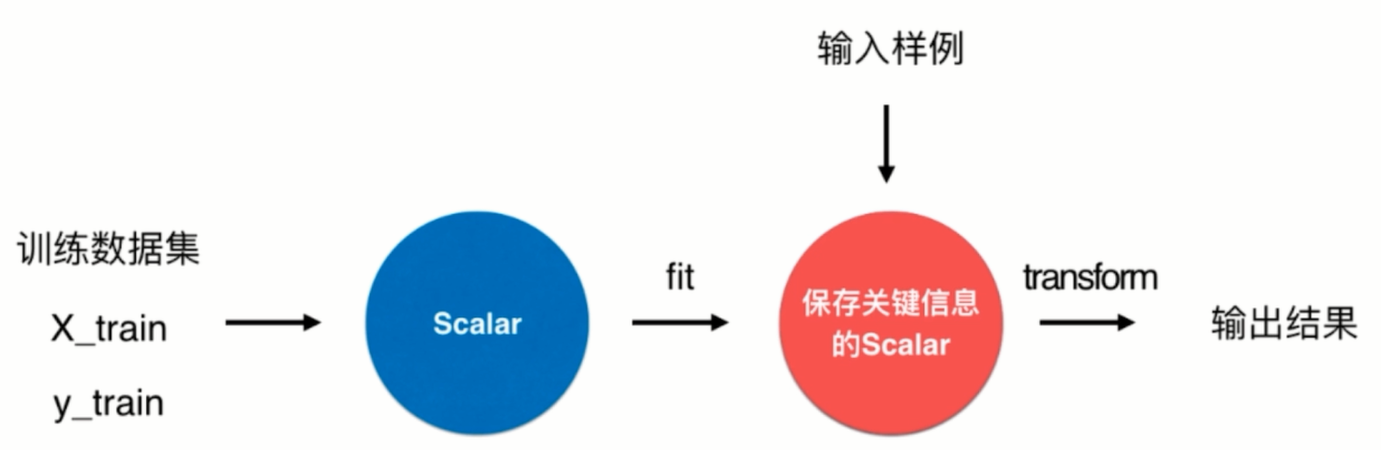
使用sklearn中的Scaler类对数据进行归一化
Scaler类的使用流程
![]()
代码示例:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris() # 加载鸢尾花数据集
X = iris.data # 特征数组
y = iris.target # 标签向量
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=666)
standardScaler = StandardScaler() # 实例化这个类
standardScaler.fit(X_train)
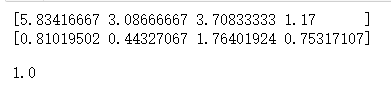
print(standardScaler.mean_) # 根据训练数据集算出的均值向量
print(standardScaler.scale_) # 根据训练数据集算出的方差向量
X_train_new = standardScaler .transform(X_train) # 对训练数据特征数组进行归一化
X_test_new = standardScaler.transform(X_test) # 对测试数据特征数组进行归一化
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train_new, y_train)
knn_clf.score(X_test_new, y_test) # 当训练数据集进行了数据归一化,那么测试数据集也必须进行数据归一化
运行结果:
![]()
![]()
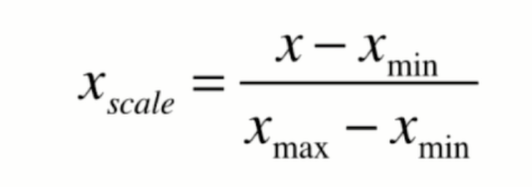
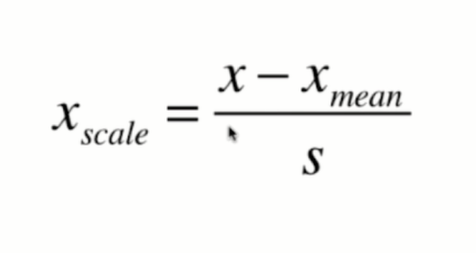




 浙公网安备 33010602011771号
浙公网安备 33010602011771号