超参数:算法运行前需要决定的参数
模型参数:算法运行过程中学习的参数
我们常说的“调参工程师”调试的基本都是超参数,超参数选择的好与坏在一定程度上决定了整个算法的好坏。
就拿KNN算法中的超参数K来说,虽然sklearn中对于KNN算法有默认的K=5,但这仅仅是在经验中得到的较为理想的值,在实际应用中却并不一定是这样。
我们就拿KNN算法来对手写数字数据集进行分类这件事来说,试图从[1-20]之间找到最合适的那个K
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits_df = datasets.load_digits()
X = digits_df.data
y = digits_df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.3, random_state=666)
best_K = 0
best_scope = -1
for k in range(1, 21):
KNN_cls = KNeighborsClassifier(n_neighbors=k)
KNN_cls.fit(X_train, y_train)
temp_scope = KNN_cls.score(X_test, y_test)
if temp_scope > best_scope:
best_scope = temp_scope
best_K = k
print(best_K)
print(best_scope)
最终的运行结果是 best_K = 3 best_scope = 0.9761526232114467 由此可见,算法中封装的默认超参数并不一定是最好的。
有一个问题我们需要注意一下: 比如说我们从[1-20]之间来寻找K,如果最终结果显示最优K为20,那么我们应该继续向上拓展,继续寻找,比如[20-30]
原因是:通常来讲,不同的超参数决定不同的分类准确率,且这个变化是连续的,如果我们最终找到的超参数位于边界,那么理论上还存有更优解我们仍未找到。
隐藏的超参数
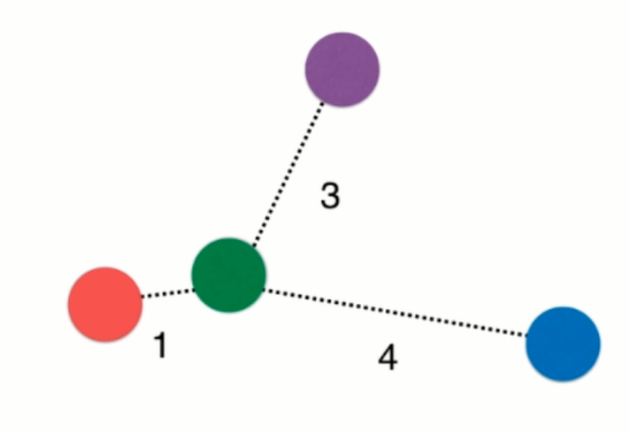
就拿KNN算法来说,如果我们的K=3,且恰巧这个待分类样本周围最近的3个样本却分属不同的三个分类(如下图所示),那么就会造成平局。
![]()
所以说,只是考虑K这一个超参数是不稳妥的,如上图所示,虽然待分类的小球最近的3个小球分属不同的分类,但是它离没一个小球的距离却不一样,我们可以认为,离得近的权重大,离得远的权重小,这样就很好的解决了平票的问题。
![]()
下边我们考虑权重再来查找一次最优的K
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits_df = datasets.load_digits()
X = digits_df.data
y = digits_df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.3, random_state=666)
best_K = 0
best_scope = -1
basic_weights = ''
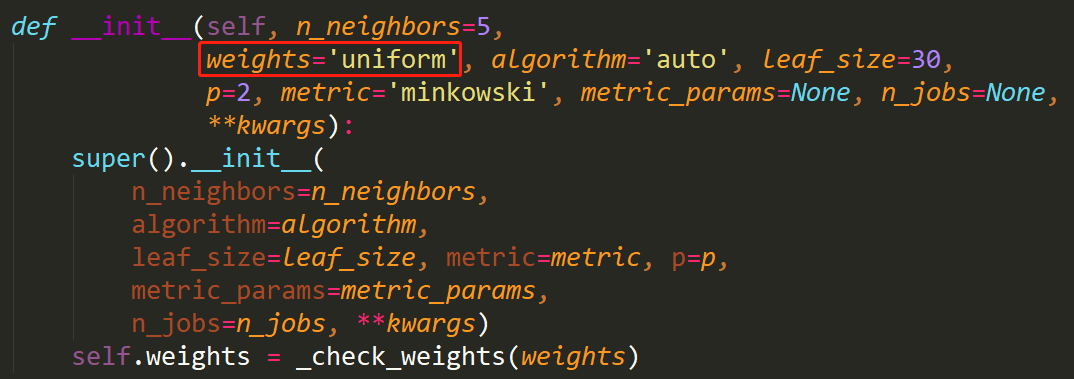
for i in ['uniform', 'distance']:
for k in range(1, 21):
KNN_cls = KNeighborsClassifier(n_neighbors=k, weights=i)
KNN_cls.fit(X_train, y_train)
temp_scope = KNN_cls.score(X_test, y_test)
if temp_scope > best_scope:
best_scope = temp_scope
best_K = k
basic_weights = i
print(best_K)
print(best_scope)
print(basic_weights)
最终结果:best_K = 4 best_scope = 0.9785373608903021 basic_weights = 'distance'
从上边我们根据是否考虑距离的权重计算出了更高的分类准确率,在这里我们不禁想到,不同的特征样本之间的距离是怎样算出来的呢?计算距离有多种方法,如欧拉距离、曼哈顿距离,不同的方法计算出的距离也不一样,这样就又引出了KNN算法中又一个超参数: KNeighborsClassifier类中的参数p
![]()
KNN算法中计算距离使用的是明可夫斯基距离,从上边的推导式可以看出,不同的o值对应不同的公式,当p=1时,计算距离用的就是曼哈顿距离,当p=2时,用的就是欧拉距离,在KNN算法中默认p=2,使用的是欧拉距离。
接下来我们再根据不同的计算距离公式来找出最优的K
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits_df = datasets.load_digits()
X = digits_df.data
y = digits_df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.2, random_state=666)
best_K = -1
best_scope = -1
best_p = -1
for i in range(1, 6):
for k in range(1, 21):
KNN_cls = KNeighborsClassifier(n_neighbors=k, weights='distance', p=i)
KNN_cls.fit(X_train, y_train)
temp_scope = KNN_cls.score(X_test, y_test)
if temp_scope > best_scope:
best_scope = temp_scope
best_K = k
best_p = i
print(best_K)
print(best_scope)
print(best_p)
我们看到 best_K=4 best_scope=0.9770514603616134 best_p=4
根据上边的代码 我们能看到,在参数p和参数k两层循环下,我们相当于在x轴为k,y轴为p的平面中遍历每一个点,来寻找其中的最优解,这中搜索策略其实有一个名字,叫做网格搜索。
上边几个例子都是我们来控制代码寻找不同的超参数,实际上,sklearn为这种网格搜索方式封装了一个专门的函数:Grid Search,下边我们使用Grid Search来执行一边函数就找到最优的几个超参数解。
先来看这个参数,它是一个list格式的参数,里边的每一个元素都是json类型,仔细看,这每一个json元素就是我们定义的一个针对超参数的搜索策略
param_grid = [
{
"weights":["uniform", "distinct"],
"n_neighbors":[ i for i in range(1, 20)]
},
{
"weights":["distinct"],
"n_neighbors":[ i for i in range(1, 20)],
"p":[ i for i in range(1, 20)]
}
]
下边调用Grid Search函数来找出最优解
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
digits_df = datasets.load_digits()
X = digits_df.data
y = digits_df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.4, random_state=666)
from sklearn.model_selection import GridSearchCV # 这个类用来进行网格搜索
knn_clf = KNeighborsClassifier() # 实例化KNN类
grid_search = GridSearchCV(knn_clf, param_grid) # 传入两个参数:模型的类,前边制定的网格搜索策略
grid_search.fit(X_train, y_train) # 先让这个类基于我们设定好的搜索策略从训练数据种找出最优的参数
grid_search.best_estimator_ # 它用来返回找到的最优超参数
这是运行结果
![]()
我们可以看到,程序已经帮我们找到了 最优的n_neighbors=4, p=7, weights='distance',我们还可以通过调用grid_search.best_score_方法来看到使用这些超参数后的分类准确度
我们如何才能获取到找到的这几个超参数呢? 使用 grid_search.best_params_ 就可以获取到通过网格搜索找到的这几个超参数
![]()
像这几个属性:grid_search.best_estimator_
grid_search.best_score_
grid_search.best_params_
上边这几个几个属性都有一个下划线(这是一种代码规则:如果某个参数是根据用户传入的参数计算出来的,那么就会带个下划线)
上边我们就已经计算出了几个最优超参数,现在我们就用最优超参数来计算一下分类准确度吧
使用sklearn为我们封装的GridSearchCV先进行网格搜索寻找最佳超参数,然后使用找到的超参数来计算进行分类并得到分类准确度:
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
digits_df = datasets.load_digits()
X = digits_df.data
y = digits_df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.3, random_state=666)
knn_clf = KNeighborsClassifier()
params_grid = [
{
"weights":["uniform", "distance"],
"n_neighbors":[i for i in range(1, 20)]
},
{
"weights":["distance"],
"n_neighbors":[i for i in range(1, 20)],
"p":[j for j in range(1, 6)]
}
]
grid_search = GridSearchCV(estimator=knn_clf, param_grid=params_grid)
grid_search.fit(X_train, y_train)
knn_clf = grid_search.best_estimator_ # 它返回的就是一个使用了最佳超参数的KNN分类器,可以直接对测试数据集进行预测
print(knn_clf)
knn_clf.score(X_test, y_test) # 直接进行预测
这是运算结果
![]()
上边我们使用了 GridSearchCV 这个类来使用网格搜索来寻找超参数,我们向这个类中传递了两个参数estimator和param_grid,estimator标识你要使用的算法类,param_grid标识要使用的网格搜索策略,其实GridSearchCV类还有一些其他的参数也是比较有用的:
![]()
因为我们使用的网格搜索有多条策略,在寻找最优超参数时就需要一条策略一条策略的去计算,这无疑是比较慢的,n_jobs参数正式为了改善这一情况的,n_jobs参数默认为None,表示只用一个cpu核心去计算,你输入数字几,它就用几核心,当n_jobs=-1时表示使用cpu的全部核心,这样就加快了计算速度。
而且在进行网格搜索时,默认是没有任何log打出的,这不利于我们观察和监督,verbose=0参数用来控制log的打印长度,数字越大,log打印的越详细
上边我们使用sklearn的GridSearchCV类找到了KNN算法常用的超参数,但这不是全部,其实KNN算法还有好多超参数,如果我们不是用明可夫斯基距离计算样本之间的距离,还有其他的一些选择:
![]()
![]()
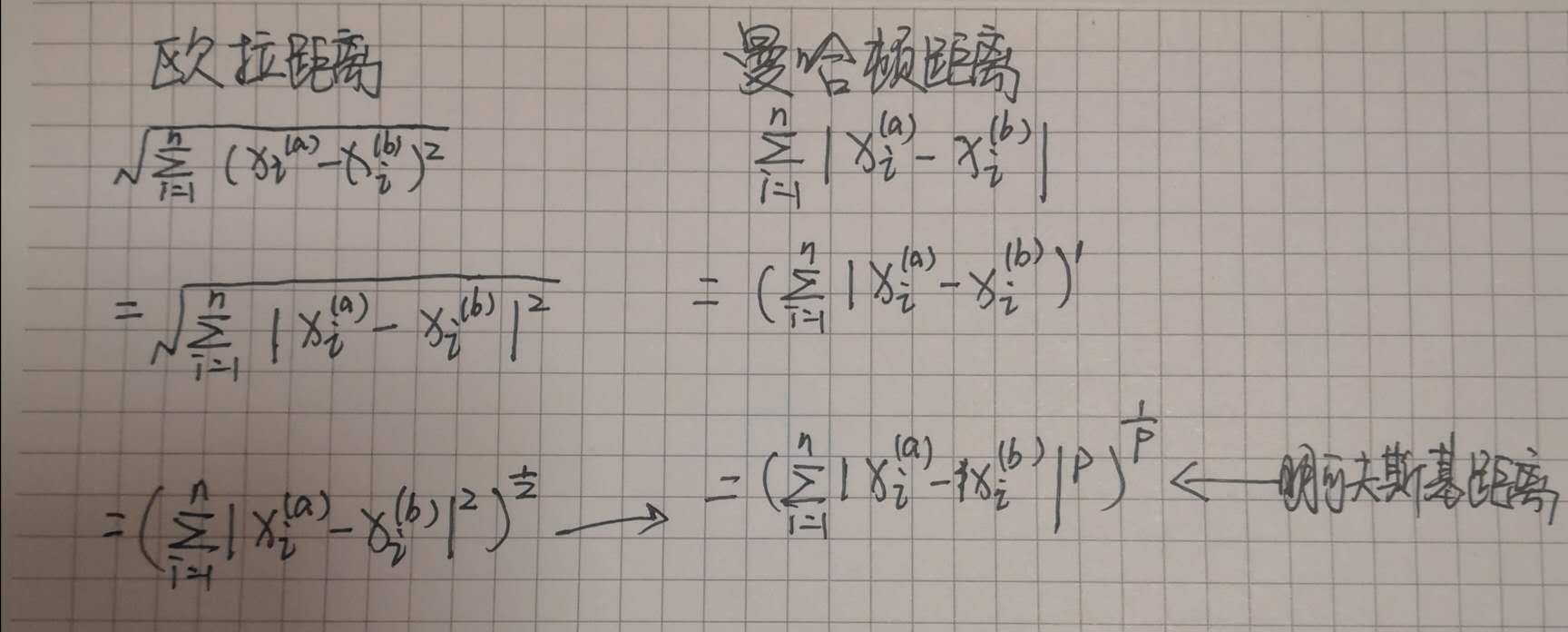








 浙公网安备 33010602011771号
浙公网安备 33010602011771号