全国大学生数学建模竞赛2021C题(部分公式未展示)
基于混合整数模型的企业订购与转运方案研究
摘要
本文针对生产企业原材料的订购与运输问题展开研究,按照企业的不同需求,分别建立了LFRM模型、0-1型混合整数规划模型对不同问题进行求解,结合生产函数和决策树算法给出了企业的订购方案及转运方案。
对于问题1,从时间限制和评分标准两方面考虑,采用数据分析和评价模型相结合的方法对企业重要性进行了量化。首先,根据供应商的订货与供货比和供应量分布筛选出6家重要的A材料供应商、7家B材料供应商和6家C材料供应商,将这23家供应商直接认定为重要供应商。其次,对余下379家供应商的重要性建立LFRM模型进行评估,选取损耗率、采购成本、订货量和供货率作为评价指标,采用熵值法确定各指标的权重系数,运用MATLAB对LFRM模型进行求解,给出各个供应商的重要性评分。最后,根据A、B、C三类原材料供应商的占比确定其余27家重要供应商。计算结果显示, 在50家重要供应商中纳入了9家A类原材料供应商,包括S145、S243等;10家B类原材料供应商,包括S138、S392等和8家C类原材料供应商,包括S384、S020等。
对于问题2,首先,将选择最少的供应商供货问题转化为0-1型混合整数规划问题。以402家供应商选择与否和供应商每周供应A、B、C类原材料的数量为决策变量,以供应商总数最少为目标,以企业产能条件、供应商的供货能力限制为约束条件构建了0-1混合整数规划模型。假定各家供货商的供货能力基本稳定,并以每家供应商240周内的平均供货量(供货量为零的不计入平均)近似表示供应商的供货能力,将模型进行简化。利用Lingo软件解得,至少22家供应商(7家A类、7家B类和8家C类)才能满足企业的材料需求。其次,在选定供应商的基础上,以需求条件、转运限制等为约束,建立优化模型,求解得到最经济的订购方案。计算结果表明,8家转运商的总损耗率以T5转运商损耗最小。由转运损耗率排名优先顺序选择损耗小的转运商,以每家转运商一周不超过6000立方米为约束确定转运方案。与企业原方案1-24周的转运方案比较,此方案未来24周共需总费用为1152730.6元,较原方案节省约11万元。
对于问题3,采用决策树算法,选取5种影响实施方案的因素,即实施方案的类型(订购方案、转运方案)、原材料类别、原材料的订购单价、转运损耗率和转运能力。将影响因素划分到决策树的不同层次区域,并对其进行评价。利用熵和Gimi系数对信息纯度进行度量,求出影响因素对实施方案的信息增益,之后通过决策树叶子节点对各个方案的基本信息进行交叉验证,确立评价函数对A、B、C三类原材料供应商进行调整,得到新的实施方案,与原方案比较,24周的损耗率降低了15.4%。
对于问题4,采用生产函数法计算企业每周产能增长率,考虑供货量、订货量、损耗率等因素在企业提高产能的影响情况。将供应商供货量、企业订购量及转运商损耗率作为生产函数的解释变量,建立生产函数模型。之后将生产函数两端取对数,进行解释变量相关性检验,确定各解释变量之间相关性。最后做解释变量的回归分析得得到,企业产能增量为5640立方米/周。
关键词:LFRM模型 0-1规划模型 订货与转运策略 决策树算法
1. 问题的重述
1.1 问题背景
某个建筑和装饰板材的生产企业,所用到的主要原材料是木质纤维和其他植物素纤维材料,大体可以分为A,B,C三种类型。该企业每年按照48周进行生产,需要提前安排24周的原材料订购及转运计划,即根据产能决定需要订购的原材料供应商(称作“供应商”)和每周相应的原材料订购数量(称作“订货量”),确定第三方物流公司(称作“转运商”)并委托其将供应商每周的原材料供货数量(称为“供货量”)转运到企业仓库。
该企业每周产出2.82万立方米产品,每立方米产品需耗费A类原材料0.6立方米,或B类原材料0.66立方米,或C类原材料0.72立方米。由于原材料较为特殊,供应商不能确保严格按照订货量供货,实际供货量可能大于或小于订货量。为了确保正常生产,该企业需要尽可能维持不少于满足两周生产需求的原材料库存量,因此该企业对供应商实际提供的原材料常常全部收购。
在实际转运过程中,原材料会有一定量的损耗(损耗量占供货量的百分比称作“损耗率”),转运商实质运送到企业仓库的原材料数量称作“接收量”。每家转运商的运输能力为6000立方米/周。通常情况下,一家供应商每周供应的原材料尽可能由一家转运商运输。
原材料的采购成本会直接影响企业的生产效益,实际上A类和B类原材料的采购单价分别比C类原材料高出20%和10%。三类原材料单位运输和储存的费用相同。附件1中给出了该企业近5年402家原材料供应商的订货量和供货量数据。附件2中给出了8家转运商的运输损耗率数据。
1.2 问题的提出
1.根据附件1,对402家供应商的供货特征进行量化分析,建立反映保障企业生产重要性的数学模型,在此基础上确定50家最重要的供应商,并在论文中列表给出结果。
2.参考问题1,该企业应至少选择多少家供应商供应原材料才可能满足生产需求?针对这些供应商,为该企业制定未来24周每周最经济的原材料订购方案,并据此制定损耗最少的转运方案。试对订购方案和转运方案的实施效果进行分析。
3.该企业为了压缩生产成本,现计划尽量多地采购A类和尽量少地采购C类原材料,以减少转运及仓储的成本,同时希望转运商的转运损耗率尽量少。请制定新的订购方案及转运方案,并分析方案的实施效果。
4.该企业通过技术改造已具备了提高产能的潜力。根据现有原材料的供应商和转运商的实际情况,确定该企业每周的产能可以提高多少,并给出未来24周的订购和转运方案。
2. 问题的分析
2.1 对问题1的分析
对于问题1,由于各个供应商在不同时间的供货量不同且分布不均,考虑到一些供货商一年只在几周对企业进行大量供货,该类企业在进行量化评估时得分并不会很高,但其重要性不可忽视。为避免该类现象发生,本文采用数据筛选与量化评估相结合的方法确定50家最重要的供应商。首先对附件1中的数据进行处理,根据数据特征筛选出部分重要的供应商,之后对余下的供应商进行量化评估。
供应商对企业的重要程度,即得出各个供应商的综合得分。计划构建评价指标体系,之后确定各指标权重系数,建立LRFM模型求解。首先需要根据实际情况和现有数据确定评价指标,计划采用四个评价指标对供应商进行评估:损耗率、采购成本、订货量、供货率。由于RFM模型中具有典型的R、F、M三个影响因素,且可以作为供应商供应能力的重要手段,预计采用FRM模型,在该模型的基础上进行改进,根据评价指标建立合适的LRFM模型;其次对评价指标进行规范化处理,之后确定指标的权重系数,最后对模型进行求解得到余下供应商的得分排名。由于A、B、C三类供应商占比不同,得出排名后根据各类材料占比得到剩余27家最重要的供应商。
2.2 对问题2的分析
对于问题2,可以将其拆分为三个问题:供应商的最少数量、花费最少的原材料订购方案、损耗率最小的转运方案。最后对订购方案和转运方案的实施效果进行分析。
在已知各个供应商供货量的基础上,给出最少选择多少家供应商才能满足企业正常的生产需求。对于供应商,只有用或不用两种情况,将该问题转化为0-1整数规划问题。以最少的供应商数量为目标函数,决策变量为402家供应商,供应商根据原材料可以分为A、B、C三类,接着考虑约束条件,该企业每周的产能为28200立方米,供应商提供的原材料应满足企业生产需求,保证企业正常生产。其次,还需要考虑到,该企业每周的产能可以由A、B、C三种不同的材料满足生产材料的需求,考虑到供货期间可能发生供货不足的情况,当只能提供需要A、B、C这三种生产材料中的一种时,仍要保证企业正常的生产,则A、B、C三种原材料的库存量不得少于能够满足两周生产需求的原材料库存量。
为该企业制定未来24周中每周最为经济的原材料订购方案,此时不仅要考虑供应商的供应能力,还需要考虑企业的经济效益,即尽量做到花的钱越少越好。决策变量不变,优化的目标为使花费的钱数最少,即目标函数指花费最少;约束条件需要考虑以下几点:由于实际中A类和B类原材料的采购单价分别比C类原材料高20%和10%,且三A、B、C类原材料运输和储存的单位费用相同,所以我们要尽可能多的选择C类原材料;又由于产生每立方米产品消耗的C类材料最多,并且至少需要满足两周生产所需的库存量。
根据最经济的原材料订购方案,制定损耗最少的转运方案,这同样是一个优化问题,优化的目标为转运损耗率最少,最后利用Lingo软件对模型进行求解,得出模型的最优解。
2.3 对问题3的分析
对于问题3,属于一个多目标决策的问题,要同时满足压缩成本、减少转运及仓储的成本、降低转运商的损耗率等多种要求,由于决策树算法具有准确性高、便于理解、可以清晰的显示影响因子、可以同时处理不同目标等优点,预计使用决策树算法进行方案的求解。将这个问题进行综合考虑,由于转运商的数量较少,确定了订购方案就相当于确定了转运方案。订购方案和转运方案都归结为实施方案,先找出订购方案和转运方案的影响因素,之后分别将影响订购方案的因素和影响转运方案的因素提取出来,对其进行评价。影响订购方案的因素有原材料的类别和订购单价;影响转运方案的影响因素有转运损耗率和转运能力,其中,转运能力不能超过6000立方米/周。将其代入决策树对多种情况进行评价,通过决策树将影响因素划分为不同的区域,确定一个评价标准,最后根据评价标准去评判所给的实施方案是否可行。给出新的订购方案和转运方案,并对其实施效果进行分析。
2.4 对问题4的分析
对于问题4,企业当前的产能能力为28200立方米/周,需要确定该企业每周产能的提高量,可以从两方面考虑:计算出企业技术改造后的产能能力,用改造后的产能能力减去当前的产能能力就得出了企业产能的提高量;计算企业产能的增长率。从现有的原材料供应商和转运商的数据,要想计算出产能量,既要计算供应商的供应量,又要计算转运商的转运量,转运商的运输能力为6000立方米/周,8家转运商的运输能力就是48000立方米/周,企业不可能同时使用八家供应商,在运输的过程中还需要考虑损失率,计算量非常大。所以预计选择后者对企业产能进行计算,通过查阅文献,采用专家评议法(delphi)选择一种适合于计算产能增长率的方法,由于生产函数法可以使数据具有可得性,而且适用性高,所以采用生产函数法对企业产能的增长率进行计算,最终可以直接用产能的增长率计算出企业的产能增量。
3. 模型的假设
针对题干信息,结合附件中的数据,全面考虑供应商供货量、企业订货量、转运商损耗率等因素对于订购方案及转运方案的影响情况,同时考虑以上各种因素对建模的影响,列出以下假设:
(1) 假设所给数据真实可靠,具有代表性;
(2) 假设企业对原材料的需求量在短时间内不会有重大变化;
(3) 假设供应商对该企业的供货稳定,不会出现不供货情况。
4. 符号说明
表1 符号说明
|
符号 |
含义 |
|
供应商第周向企业供应的A类原材料量 |
|
|
供应商第周向企业供应的B类原材料量 |
|
|
供应商第周向企业供应的C类原材料量 |
|
|
供应商第周的供货能力 |
|
|
A、B、C类原材料的采购单价 |
|
|
材料运输、储存的单位费用 |
|
|
第周供应商供货量对产能的影响 |
|
|
第周企业订货量对产能的影响 |
|
|
第周转运商损耗率对产能的影响 |
|
|
|
权重系数 |
|
检验过程的学习率 |
|
|
N |
周数 |
|
企业产能的增长率 |
5. 模型的建立与求解
5.1 问题1的建模与求解
从402家供应商确定最重要的50家供应商,首先针对附件1的数据进行处理,将供应A、B、C三类原材料的供应商进行分类(如图1所示),共有146家A类材料供应商、134家B类材料供应商和122家C类材料供应商,分别占供应商总数的36%、33%、31%。
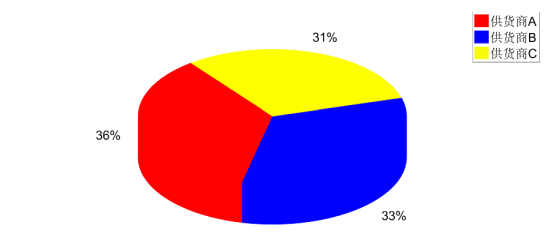
图 1 三类原材料供应商占比
供应商的重要性为一个模糊的概念,本文选取多个指标对其进行刻画,并建立LFRM模型进行求解,得出每个供应商综合得分,根据得分排名及各类占比确定50家最重要的供应商。在对数据整理时发现,供应商在供货时并不是每周都供货,跟一年的时间有一定的关系,有的供应商可能一年中只有几周有大量货物可供订购即供货数量与时间有一定关系,且该周货物占该企业需求的比重很大,在进行重要性评估时,由于评价指标对供应商重要性的影响较大,如将所有供应商都运用评价系统进行评分,显然,上述供应商综合得分因供货次数少其分数会低于其他供应商,而在实际上,该类供应商的重要性无可替代。因此,为避免这类现象发生,本文在对供应商进行评价建模前,对数据进行筛选,筛选出一部分重要的供应商,之后对其余供应商进行重要性评估,选出剩余重要的供应商。
5.1.1数据筛选
对附件1数据进行分类后,分别算出各个供应商在五年(240周)内的供货总量及其占比,之后根据供货总量对供应商进行排序,其次计算出每行数据中0的占比,在附件1中,0表示该周该供货商未向该企业供货,0的占比越大表示该供货商在五年内向企业供货的周数(次数)越少,处理后的部分数据见表2。
表 2 排序后部分数据
|
供应商ID |
材料分类 |
供货量总和 |
供货量占比 |
0的占比 |
|
S229 |
A |
354887 |
24.423% |
0 |
|
S348 |
A |
92421 |
6.360% |
0.19167 |
|
S308 |
B |
136998 |
9.141% |
0 |
|
S194 |
C |
101365 |
6.999% |
0 |
|
S382 |
C |
28 |
0.002% |
0.9375 |
根据处理过表中的数据可知,A、B、C三类供应商中都有供货占比份额较大且每周都向企业供货的,针对该类供应商,我们可以直观确定其对企业的影响是相当重要的。已知企业每周需要耗费A类原材料47000立方米,或B类原材料42728立方米,或C类原材料39167立方米。由需求总量,设定当占比超过6%时,认为该供应商对企业影响都很重要,根据此标准可选出6家A类原材料供应商:S229、S282、S275、S329、S348、S352,7家B类原材料供应商:S140、S108、S340、S139、S131、S308、S330和6家C类原材料供应商:S361、S151、S356、S268、S306、S194。
此外,供货次数少但供货总量占比相对高的供应商对企业的重要性也是不言而喻的,说明该类供货商在特定几周原材料较多,可以保障企业订单需求。通过数据可知,S201供应商0的占比达83%,供货占比为5.643%,说明过去五年(240周)中该供货商只在40周对企业提供原材料,供货占比较高,该供货商对企业也是非常重要的。此类供货商还有S395、S126、S037.综上,由数据直观给出的信息可以筛选出23家重要的原材料供应商。采用评价系统对剩余379家供应商进行评估,由综合得分排名选出剩下27家重要的供应商。
5.1.2确定LFRM模型的评价指标
在余下的379家供应商中还应找出27家,采用LFRM模型,LFRM模型是FRM模型的推广和延申,二者最大的区别在于影响因素的个数,根据题目中所给的信息可以提取出402家供应商的4个供货特征,分别为:损耗率、采购成本、订货量、供货率,将这三个供货特征作为评价供货商供货能力的评价指标,供货特征即为评价指标。需要进行量化的指标为:损耗率、订货量、采购成本、供货率。LRFM模型评价指标的具体解释如表3所示:
表 3 LRFM模型评价指标表
|
模型 |
L |
R |
F |
M |
|
LRFM |
耗损率 |
订货量 |
采购成本 |
供货率 |
5.1.3评价指标的规范处理
一般情况下,在LRFM模型的指标中,各指标可能属于不同类型、不同单位、不同数量级,如采购成本的单位为(元),而时间的单位为(周)。使得各指标之间存在着不可公度性,给模型的建立带来了诸多不便。为了尽可能地反映实际情况,消除由于各项指标间的这些差别,避免出现不合理的评价结果,就需要对评价指标进行一定的规范化处理,其中规范化处理包括一致化、定性指标定量化、无量钢化等。处理的具体准则见图2所示:

图 2 量化标尺
将定性指标转化为定量指标,将影响较大、影响大、影响一般、影响小、影响较小转化为具体数值,记作并采用1-9比例标度法来度量,可以将影响供货商重要性的4个指标分别记为
用成对比较法和1-9比较尺度构造判断矩阵
对该矩阵进行一致性时,需要利用一致性指标,为了衡量CI的大小,又引入平均随机一致性指标RI和一致性比率CR来对各判断矩阵进行一致性检验,保证最终所得权重的科学性。三者是关系为
(1)
其中,RI为平均随机一致性指标,n表示判断矩阵的阶数,RI与n有关,n越大,则出现一致性随机偏离的可能性越大,其对应关系如表4所示:
表 4 平均一致性指标RI的数值表
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
0 |
0.58 |
0.90 |
1.12 |
1.24 |
1.32 |
1.41 |
1.45 |
一般地,当时,则认为矩阵A的不一致程度在容许范围之内,利用MATLAB软件判断该矩阵是否通过一致性检验,可得
则判断矩阵A通过一致性检验。
5.1.4 确定LFRM模型的权重系数
在评价指标中,想要得到科学、公正、合理的评价结果,就必须考虑各项指标对总体目标实现的重要程度,即评价指标的权重系数。确定指标的权重系数的方法一共有三种,分别为主观赋权法、客观赋权法、综合集成赋权法。根据对这三种方法的适用程度,本文选择使用主观赋权法中的熵值法确定权重。指标特征比重为
(2)
指标的熵值为
(3)
其中,k>0为常数,通常取;不难看出,,并且的值异差越大,其熵值越小;反之,熵值越大。指标的差异系数为
(4)
这说明,如果指标的指标值差别越大,则差异系数就越大,表明指标越重要。指标的权重系数为
(5)
利用MATLAB软件(程序见附录Ⅱ)确定其权重系数为
5.1.5对LFRM模型进行求解
在确定了23个供货商的基础上,在剩下的379个供应商中利用MATLAB软件(程序见附录Ⅲ)对LFRM模型进行求解,对各个供应商进行综合评分,分数越高,表示越重要。最后对综合评分进行排序,按照A、B、C三类原材料供应商占比选出前27个评分较高的供应商如表5所示:
表 5 利用LFRM模型确定的27个供应商表
|
供应商ID |
材料分类 |
损耗率 |
订货量 |
采购成本 |
时间 |
WRSR |
|
S384 |
C |
3 |
9 |
6 |
5 |
0.9233 |
|
S243 |
A |
7 |
8 |
6 |
9 |
0.8898 |
|
|
||||||
|
S159 |
A |
9 |
8 |
8 |
4 |
0.8388 |
|
S213 |
C |
7 |
9 |
3 |
6 |
0.7657 |
|
S076 |
C |
7 |
7 |
8 |
8 |
0.7641 |
|
S135 |
C |
9 |
5 |
9 |
5 |
0.7641 |
注:此表格中指标对应数据为定量化之后的值
综上所述,最重要的50家供应商列表结果如表6所示:
表 6 最重要的50家供应商列表
|
供应商ID |
材料分类 |
供应商ID |
材料分类 |
供应商ID |
材料分类 |
|
S384 |
C |
S297 |
C |
S282 |
A |
|
S243 |
A |
S199 |
B |
S275 |
A |
|
S145 |
A |
S120 |
B |
S329 |
A |
|
S116 |
A |
S377 |
C |
S348 |
A |
|
S181 |
A |
S027 |
A |
S352 |
A |
|
S159 |
A |
S169 |
B |
S140 |
B |
|
S138 |
B |
S253 |
C |
S108 |
B |
|
S317 |
A |
S166 |
B |
S340 |
B |
|
S150 |
A |
S048 |
B |
S139 |
B |
|
S392 |
B |
S073 |
B |
S131 |
B |
|
S064 |
A |
S213 |
C |
S308 |
B |
|
S389 |
B |
S076 |
C |
S330 |
B |
|
S020 |
C |
S135 |
C |
S361 |
C |
|
S333 |
B |
S229 |
A |
S151 |
C |
|
S356 |
C |
S268 |
C |
S306 |
C |
|
S194 |
C |
- |
- |
- |
- |
5.2 问题2的建模与求解
要求在满足企业自身生产需求的基础上求解最少供应商的最优策略,将影响供应商是否供货的多种因素作为约束条件,建立整数规划模型,将该问题转化为0-1规划问题进行求解。
5.2.1确定最少的供应商数量
Step1:决策变量的确定
以分别表示402家供应商。若供应商被选择则令;否则,。另设供应商第周向企业供应的A类原材料为立方米,B类原材料为立方米,C类原材料为立方米。
Step2:确定目标函数
在企业满足自身生产需求的前提下,要求计算供应商的最少数量,则确定的目标函数为供应商数量的最小值。确定目标函数为
Step3:确定约束条件
(1)企业每周的产能约束
企业每周的产能为,每立方米产品需消耗A类原材料,或B类原材料,或C类原材料。因此,A类原材料的产能转化率为,即1立方米原材料可以生产产品立方米。类似地,B类和C类原材料的产能转化率分别为和。所有供货商第周的供货数应满足企业该周的产能需求,以周为例,该约束条件可以表示为
。
(2)供货能力限制
以和分别表示供应商第周的供货能力,则有
(3)逻辑约束
当供应商被选中后才能向企业供应A、B、C类原材料,即只有当时,才有和大于零。为了表达这一逻辑约束,设表示一个足够大的数(这里取到企业A、B、C三类原材料24周的需求上限之和即可),该约束可以表示为
。
当时,即供应商未被选中,该约束迫使供应商在所有24周内A、B、C类原材料的供货量均为零。当时,该约束实际上不起作用。
(4)非负和0-1限制
这里要求或1,而,,。
至此,建立了包含402个0-1变量,个非负变量,426个约束的混合整数规划模型。该模型可以表示为
为了简化模型的计算,假设每家供应商每周的供应能力是稳定的。以,和分别表示第家供应商的供应能力,取过去5年每家供应商每周供应A、B、C类三类原材料的平均供应量,近似表示供应商的供应能力,即令
其中分别表示供应商第周的实际供应A 、B、C的数量。,及分别表示第家供应商对A、B、C三类原材料的供应量大于0的供货次数。因每周的情况相同,故取即可,此时该模型简化为
利用Lingo软件(见附录Ⅱ)对模型进行求解,计算得到目标函数的最优值为22,即企业应至少选择22家供应商,其中供应A原料的有7家,供应B原料的7家,供应C原料的有8家。相关供应商的编号汇总于表8。选择的22家供应商结果如表7所示:
表 7 选择的22家供应商
|
供应商ID |
材料分类 |
供应商ID |
材料分类 |
供应商ID |
材料分类 |
|
S108 |
B |
S229 |
A |
S330 |
B |
|
S126 |
C |
S268 |
C |
S340 |
B |
|
S131 |
B |
S275 |
A |
S348 |
A |
|
S139 |
B |
S268 |
C |
S356 |
C |
|
S140 |
B |
S306 |
C |
S361 |
C |
|
S151 |
C |
S307 |
A |
S395 |
A |
|
S194 |
C |
S308 |
B |
- |
- |
|
S201 |
A |
S329 |
A |
- |
- |
5.2.2确定订购方案
Step1:决策变量的确定
针对上文求出的22家供应商,利用所建立的数学规划模型对企业未来的24周做出最经济的原材料订购方案。决策变量为所要研究的22家供应商,其中包括7家A类原材料的供应商、7家B类原材料的供应商和8家C类原材料的供应商。设表示第家A类供应商24周的供应量,表示第家B类供应商24周的供应量,表示第家C类供应商24周的供应量。
Step2:目标函数的确定
要得到企业未来24周最经济的原材料订购方案,就要考虑在供应商供应三种类型原料时花费最少的情况,目标函数可确立为
(6)
其中、、分别代表A、B、C三类材料的采购单价,和代表A、B、C三类材料的运输和储存的单位费用。
Step3:约束条件的确定
由于实际中A类和B类原材料的采购单价分别比C类原材料高20%和10%,即
确保订购方案最经济,要尽可能多地选择C类原材料,可得
三类原材料供货量应满足企业未来24周正常需求,企业每周产能为2.82万立方米,24周产能为67.68万立方米,根据上述原材料转化率,应有
(7)
综上所述,建立单目标规划模型为
利用Lingo软件对模型进行求解,计算得到目标函数的最优解,根据最优解得到企未来24周每周最经济的原材料订购方案,表8给出未来3周企业的订购方案,具体方案见附件A。
表 8 前三周的订购方案数据表
|
供应商ID |
材料类型 |
第01周 |
第02周 |
第03周 |
|
S108 |
B |
832 |
636 |
761 |
|
S126 |
C |
117 |
113 |
195 |
|
S131 |
B |
539 |
657 |
628 |
|
S139 |
B |
6391 |
1 |
7123 |
|
S340 |
B |
611 |
581 |
558 |
|
S143 |
A |
246 |
493 |
211 |
|
S151 |
C |
518 |
598 |
571 |
|
S194 |
C |
427 |
414 |
431 |
|
S201 |
A |
1 |
474 |
435 |
|
S229 |
A |
1548 |
1812 |
1995 |
|
S275 |
A |
414 |
585 |
621 |
|
S282 |
A |
731 |
716 |
748 |
|
S284 |
C |
6 |
82 |
54 |
|
S306 |
C |
648 |
432 |
653 |
|
S307 |
A |
1 |
3 |
4 |
|
S308 |
B |
614 |
391 |
352 |
|
S329 |
A |
737 |
821 |
818 |
|
S330 |
B |
1716 |
875 |
323 |
|
S340 |
B |
493 |
373 |
412 |
|
S348 |
A |
1 |
5 |
191 |
|
S352 |
A |
141 |
138 |
146 |
|
S361 |
C |
1321 |
1198 |
1666 |
5.2.3确定转运方案
类似于订购方案中求解最少供应商数量,转运方案需要求的是最少的转运损耗率,此时需要考虑附件2中各转运商的运输损耗率。在此基础上,制定损耗最少的转运方案,根据
(8)
计算损耗率。
根据附件2中给出的8家转运商5年(240周)的转运损耗率数据,可以发现转运商每周的损耗率不同,其各个转运商在同一周的损耗率也不一样。为增加企业生产效益,选取损耗率小的转运商。转运商在240周内耗损率为0的周数越多,说明越可靠。计算得到8家转运商在240周内0所占的比重,如表9所示:
表 9 8家转运商损耗率占比
|
转运商ID |
0所占的比重(%) |
|
T1 |
0 |
|
T2 |
0 |
|
T3 |
51.25% |
|
T4 |
57.5% |
|
T5 |
65.42% |
|
T6 |
10% |
|
T7 |
0 |
|
T8 |
15.42% |
由上表可以得到,在这8家转运商中,T5转运商损耗率为0占比达到65.42%,说明用此转运商运送货物最为实惠。转运商排名为T5、T4、T3、T8、T6、T1、T2、T7,即针对上述订购方案安排转运时,优先考虑T5转运商,其次为转运商T4,以此类推,此处给出前三周的转运方案,24周转运方案见附件B。
在第一周转运商T5需要转运11个供应商的原材料共5984立方米,转运商T4需要转运10个供应商的原材料共5678立方米,转运商T3需要转运1个供应商的原材料共6000立方米,转运商T8需要转运1个供应商的原材料共391立方米;在第二周转运商T5需要转运10个供应商的原材料共5779立方米,转运商T4需要转运12个供应商的原材料共5619立方米;在第三周转运商T5需要转运10个供应商的原材料共5789立方米,转运商T4需要转运11个供应商的原材料共5984立方米,转运商T3需要转运1个供应商的原材料共6000立方米,转运商T8需要转运1个供应商的原材料共123立方米。
5.2.4实施效果的分析
已知A类和B类原材料的采购单价分别比C类原材料高20%和10%,假设C类原材料的采购单价为1,则A类和B类原材料的采购单价分别1.2和1.1。三类原材料转运及存储费用相同,为便于计算,都设为1。
计算可得原订购及运输方案24周需要A、B、C三类原材料的总供货量分别为145572立方米、129179立方米和130962立方米,采购三种原材料分别花费174686.4元、142096.9元和130962元,共计447745.3元。转运及存储三类原材料分别需要291144元、258358元、261924元,共计811426元。则所需总费用为1259171.3元。
由上述订购方案及转运方案,计算得到24周A、B、C三类原材料的总供货量分别为135972立方米、119579立方米和121062立方米,采购这三种原材料分别需要花费145274.4元、133168.2元和121062元,共计399504.6元。存储及转运费三类原材料分别需要271944元、239158元和242124元,共计753226元。则需要花费的总费用为1152730.6元。通过计算可以得出,给出的方案比原有的方案节省106440.7元。
5.3 问题3的建模与求解
企业需要达到压缩生产成本、较少转运及仓储的成本、减少转运商转运率等多种要求,在多种复杂的决策情况中,往往需要多层次或多阶段的决策。决策树算法是一种简单易用的非参数分类器,是一种以实例为基础的归纳学习方式,从关联规则的角度看,树的各个分支就是各个规则,由此可以通过树模型的结构来为企业提供订购方案及装运方案。决策树各因素评价的示例图如图3所示:
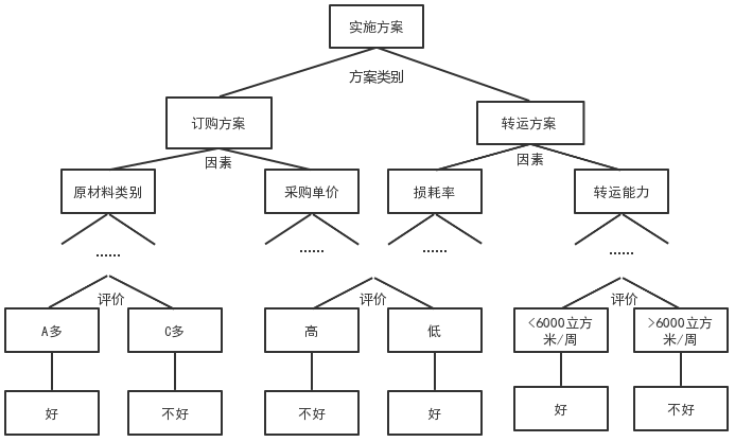
图 3 决策树各因素评价示例图
从决策树风险评级示例图可以看出,决策树将所给的影响订购方案及转运方案的因素按照不同特征划分成了不同的区域,用“好”“不好”表示企业对实施方案的评价,通过各个影响因素的属性值在决策树上由根到叶子节点测试结果,对可能影响订购方案及转运方案的因素进行评价。
5.3.1确定决策树评价函数
根据从附件及题干中提取出的5种影响因素:实施方案的类别、原材料类别、原材料的订购单价、转运过程中的损耗率、转运能力。但在实际生活中,确定一个企业要实施什么样的方案(订购方案、转运方案、决策方案等),其影响因素远大于5种,利用熵和Gini系数来对决策树信息的纯度进行度量,之后对决策树进行结合交叉验证,得到评价结果,具体评价函数即为验证过程中的损失函数,评价函数越小即损失越小,也就是考虑的因素越全面。评价函数公式[10]为
(9)
(10)
其中,R与r分别表示剪枝前后的决策树的根节点。显然,图3展示的决策树是剪枝后的决策树。
利用评价函数可以衡量该节点的重要性。例如,叶子节点原材料类别和原材料的采购单价,若采购单价的评价函数大于原材料类别的评价函数,则采购单价对于订购方案的影响较大;同理,叶子节点损耗率和转运能力,若损耗率的评价函数大于转运能力的评价函数,则损耗率对于转运方案的影响较大。
5.3.2建立决策树评判标准
以公式(9)和公式(10)的评价函数为基础,可以得到决策树的评判模型。当剪枝前后的损失函数相等时,生成函数的评判标准可表示为
(11)
其中,被看作是一个评判标准,越大则实施方案的效果就越好,当时,证明制定的新的方案是可行的。
5.3.3实施方案与实施效果
新的实施方案基于问题2中的方案来进行调整,为了尽量多地采购A类和尽量少地采购C类原材料,则我们不考虑供应原材料B的供货商,如S108、S131、S139、S140等供应商。先考虑订购方案,根据题干中,原材料的采购成本直接影响到企业的生产效益,实际中A类和B类原材料的采购单价分别比C类原材料高20%和10%这一条件,将所有供应A原材料和C原材料的供应商筛选出来,剩余供应商共计15家,其中,供应原材料A的供应商7家,供应原材料C的8家。
将决策树模型中的评价标准进行量化,根据公式(17)计算出这15家供应商的评判标准分别,并进行评判标准的排序,得到如表10所示的结果。
表 10 评判标准的结果图
|
供应商ID |
材料分类 |
采购成本 |
|
|
S194 |
C |
6 |
0.921 |
|
S201 |
A |
7 |
0.907 |
|
S229 |
A |
3 |
0.830 |
|
S275 |
A |
6 |
0.823 |
|
S282 |
A |
7 |
0.821 |
|
S284 |
C |
6 |
0.820 |
|
S306 |
C |
6 |
0.795 |
|
S365 |
C |
6 |
0.756 |
|
S143 |
A |
4 |
0.743 |
|
S151 |
C |
9 |
0.705 |
|
S361 |
C |
5 |
0.680 |
|
S126 |
C |
6 |
0.666 |
|
S348 |
A |
3 |
0.633 |
|
S352 |
A |
8 |
0.560 |
|
S361 |
C |
1 |
0.507 |
在这15家供应商中,按照“A多C少”的原则进行调整,原方案中,供应A类原材料的供应商在22个供应商中所占的比例为32%,供应C类原材料的供应商在22个供应商中所占的比例为36%,而A类原材料对于企业的消耗是最少的,对于提高企业库存有重大的影响。对转运商的损耗率进行计算,利用Excel软件做出8家供应商损耗率的柱状图,如图4所示:
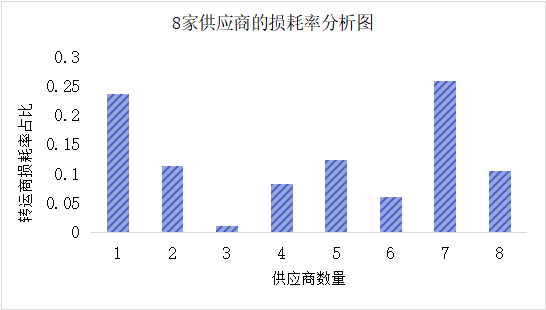
图 4 供应商损耗率的分析图
制定新的订购方案时,不单单需要考虑损耗率,还需要考虑生产成本、转运和存储成本,多种因素综合评估,根据问题2中转运商的优先顺序排序调整方案。除提供A、C类原材料的供应商之外,其余供应B原材料的供应商保持不变,调整的订购方案结果如表11所示:(具体方案结果见附件A)
表 11 调整的订购方案部分数据表
|
供应商ID |
材料类型 |
第01周供货量 |
第02周供货量 |
第03周供货量 |
|
S108 |
B |
832 |
636 |
761 |
|
S201 |
A |
56 |
89 |
134 |
|
S131 |
B |
539 |
657 |
628 |
|
S139 |
B |
6391 |
1 |
7123 |
|
S340 |
B |
611 |
581 |
558 |
|
S348 |
A |
407 |
429 |
455 |
|
S194 |
C |
427 |
414 |
431 |
|
S201 |
A |
1 |
474 |
435 |
|
S229 |
A |
1548 |
1812 |
1995 |
|
S275 |
A |
414 |
585 |
621 |
|
S282 |
A |
731 |
716 |
748 |
|
S284 |
C |
6 |
82 |
54 |
|
S306 |
C |
648 |
432 |
653 |
|
S307 |
A |
1 |
3 |
4 |
|
S308 |
B |
614 |
391 |
352 |
|
S329 |
A |
737 |
821 |
818 |
|
S330 |
B |
1716 |
875 |
323 |
|
S340 |
B |
493 |
373 |
412 |
|
S348 |
A |
1 |
5 |
191 |
|
S352 |
A |
141 |
138 |
146 |
|
S143 |
A |
1421 |
1098 |
1032 |
结果表明,在新的转运方案中,A类原材料供应商数量远大于C类原材料供应商数量,通过计算可得有选择转运商T5的概率为56.4%,相较于原方案提高15.4%,令转运商的损耗率得以降低。由此可见,新方案更具实用性。所以企业应当实时进行方案的调整,以达到提高经济效益和降低损耗率的效果。
根据该订购方案制定出新的转运方案,8家转运商按照供应量的多少进行调整,调整的具体结果见附件B。此处给出前三周的转运方案:
在第一周转运商T5需要转运15个供应商的原材料共5053立方米,转运商T4需要转运3个供应商的原材料共3678立方米;在第二周转运商T5需要转运10个供应商的原材料共5929立方米,转运商T4需要转运8个供应商的原材料共5019立方米;在第三周转运商T5需要转运9个供应商的原材料共5789立方米,转运商T4需要转运7个供应商的原材料共5324立方米,转运商T3需要转运1个供应商的原材料共6000立方米,转运商T8需要转运1个供应商的原材料共237立方米。
5.4 问题4的建模与求解
5.4.1生产函数模型构建
根据现有的原材料供应商和转运商的实际情况,全面考虑供货量、订货量、损耗率等因素在企业提高产能的影响情况,采用生产函数法进行企业产能增长率的计算,通过增长率计算产能的增量。以柯布-道格拉斯生产函数[8]为基础,以供货量、订货量、损耗率为解释变量,建立生产函数:
其中,表示企业产能的增长率(%);表示第周供应商供货量对企业产能的影响;表示第周企业订货量对企业产能的影响;表示第周转运商的损耗率对企业产能的影响。对附件1中数据进行计算,得到对本题有效的数据集如表12所示:
表 12近五年的解释变量表
|
周数 |
供货量 |
订货量 |
损耗率(%) |
|
1 |
16136 |
18492 |
0 |
|
2 |
17897 |
19304 |
0 |
|
3 |
18328 |
18892 |
0 |
|
102 |
21011 |
20925 |
5 |
|
103 |
13193 |
19658 |
0 |
|
238 |
27892 |
27913 |
0 |
|
239 |
19150 |
19127 |
0 |
|
240 |
17332 |
21027 |
0 |
将生产函数两端取对数,同时对指标的原始数据取自然对数,可以得到
对表中的数据进行取对数的计算可以得到如表13所示的结果。
表 13 取自然对数后的数据表
|
周数 |
供货量 |
订货量 |
损耗率(%) |
|
1 |
9.68880808 |
9.825093485 |
- |
|
2 |
9.79238838 |
9.868067607 |
- |
|
3 |
9.816185224 |
9.846493831 |
- |
|
102 |
9.571574905 |
9.985850643 |
1.609437912 |
|
103 |
9.777867639 |
9.959111456 |
- |
|
238 |
9.750336373 |
9.870757728 |
- |
|
239 |
10.07861664 |
10.0856841 |
- |
|
240 |
9.545812108 |
9.994424548 |
- |
在进行回归分析之前,首先进行解释变量相关性系数的检验,由相关系数检验可以得到各解释变量之间高度相关。之后利用Eviews软件,做解释变量的回归分析可以得到:在、、中,与的一元回归可以达到最高,且。
根据企业产能的增长率,可以计算出该企业每周的产能增量为
5.4.2确定订购和转运方案
根据企业每周的产能增量可以确定当前企业每周的产能为33840立方米/周,所要确定的实施方案(订购和转运方案)和上文中唯一的不同之处,在于企业每周的产能发生了改变,由原来的28200立方米/周增加到33840立方米/周,订购和转运方案的确定以问题3为基础,根据问题3,给出问题4的订购和转运方案,由于数据较多,而且不具有规律性,在此不做展示,具体方案结果见支撑材料。
6. 模型的检验
6.1 问题1的检验
对于问题1设立的评价指标,使用相对比较法对评价指标权重系数,首先将所有的评价指标分别按行和列排列,构成一个正方形数表,根据0,0.5,1三级比例标度对指标进行两两比较,令指标与比较的相对评分为
. (12)
根据相对重要程度将评分值得到评分矩阵,显然,。最后做归一化处理,利用
(13)
求得指标的权重系数分别为
0.3125,0.1875,0.3125,0.1875
重新确定权重系数后,再次带入模型,得到各类供应商新的综合得分排名,按照三类原材料供应商比例选取27家,与之前进行对比发现,仅有四家供应商发生变化,数量相对较少,说明该模型较为稳健,具有说服力。
6.2 实施方案的检验
根据所给出的订购方案和装运方案,采用BP神经网络对实施方案进行检验。通过多层反馈调整,判断确立的数学规划模型是否合理。BP神经网络结构图如图5所示:
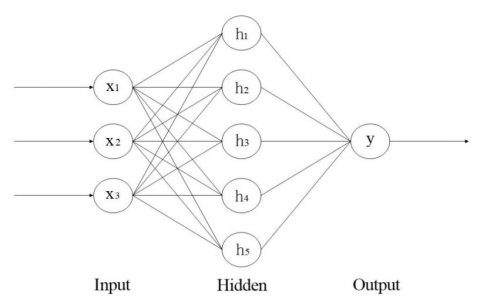
图 5 神经网络结构图
数据从输入端进入,信号正向传播时,对于给定的参数集合通过激活函数计算输出结果,本文采用Sigmoid函数进行激活,将神经网络的误差进行反向传播采用批量梯度下降法对网络进行求解,对于本文的数据集,定义整体代价函数
其中,为权重衰减参数。
采用梯度下降法每一次迭代都按照如下公式对参数进行更新,得到
其中是学习率。通过梯度下降函数对参数进行调节,使误差极小化,误差越小,预测的结果就会越好。利用MATLAB软件求解模型的准确率,可以得到如图5所示的模型准确率的趋势图。
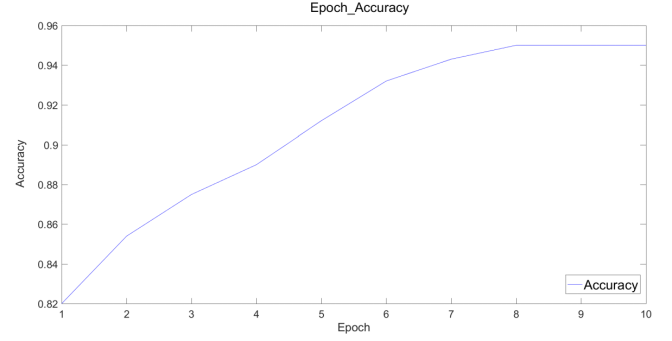
图 6 模型准确率的趋势图
由图6可以看出,模型的准确率逐渐升高,最后可以达到95%左右,故建立的数学规划模型较为合理,证明所给出的实施方案具有可行性。
7. 模型的评价与推广
7.1 模型的优点
1、本文运用LFRM模型,根据实际评价指标,建立更适用于本题的量化评估系统;
2、建立0-1规划模型使问题2更为清晰,可以根据其决策变量、目标函数、约束条件得到最优解,求解准确。本文将供应商供货能力、企业产能等作为约束条件,得到最为经济的目标函数,利用 MATLAB 进行求解;
3、建立的模型能够与实际紧密联系,结合实际情况对问题进行求解,使得模型具有很好的通用性和推广性;
4、创建了决策树模型建立评价函数,通过对附件数据信息的分析,找到供应商、企业、供货商之间的联系,使得评价函数更贴切实际。
7.2 模型的缺点
1、本文计算过程使用附件中数据,数据来源有限,模型准确度无法进行进一步的评估,模型具有一定的局限性;
2、决策树模型容易调整考虑样本数据从而失去稳定性。
7.3 模型的推广
1、数学规划中的0-1规划模型可以将复杂模型简单化,应用领域十分广泛,在指派问题、分配问题及选址问题中均可以使用;
2、LFRM模型是基于FRM模型建立的,可用于对企业、公司等进行综合评价,相较于基础模型,适用范围更广,适用性也更强。
参考文献
[1]王鹏,张静宇,石文,宇文宗辉,师帅.基于决策树算法的古代方剂分类研究[J].信息与电脑(理论版),2021,33(10):45-48.
[2]周莉,李静毅.基于决策树算法的联级网络安全态势感知模型[J].计算机仿真,2021,38(05):264-268.
[3]赵文隆,龚俊,马俊辉,张晓飞,黄洁,魏静.基于决策树算法的复合包装膜袋材质鉴别[J].包装工程,2020,41(21):93-102.
[4]严洋洋,殷志祥.基于DNA折纸系统求解0-1整数规划问题的模型[J].绵阳师范学院学报,2020,39(05):85-90.
[5]郭继东,张开彬,江俊豪,梁钰艳,冯彩萍,周大为.基于程序分析和0-1整数规划模型的1号车间生产线平衡改善设计[J].机电工程技术,2020,49(02):12-16+64.
[6]方为志.多肽缓释体系RADAmx/FRM的构建及治疗大鼠脊髓损伤的研究[D].华中科技大学,2018.
[7]史方明.基于FRM信道化技术研究[D].哈尔滨工程大学,2018.
[8]李禹萱.中国半导体行业发展影响因素的实证研究——基于柯布-道格拉斯生产函数的回归分析[J].科技和产业,2021,21(06):83-86.
附录
附录Ⅰ支撑材料目录
1. pingfen.m
2. question1.m
3. ss3.xlsx
4. 附件A 订购方案数据结果.xlsx
5. 附件B 转运方案数据结果.xlsx
6. 供货商最少.lg4
7. 剩下379个数据构成矩阵.xlsx
8. 问题1处理后的数据.xlsx
附录Ⅱ代码
问题1中求判断矩阵的权重代码
|
问题1中求评价指标的综合评分程序
|
clc;clear; R2=xlsread('379个随即数.xlsx'); %将处理后的表读入MATLAB软件 [n,m]=size(R2) w_jfjcfq=[0.5323 0.2884 0.0675 0.1118]; ra=tiedrank(R2); W=repmat(w_jfjcfq,[n,1]); %计算评价得分 WRSR=sum(ra.*W,2)/n [WRSR,ind]=sort(WRSR); |
问题2中求目标函数最优解代码
|
model: sets: Supply/1..402/:X;!定义供货商集合,X表示供货商是否选择; Week/1/:;!定义周数集合; Link(Supply,Week):XIJA,XIJB,XIJC,SIJA,SIJB,SIJC;!XIJA,XIJB,XIJC分别表示A、B、C类原材料的供货量,SIJA,SIJB,SIJC表示供应商的供货能力; endsets data: SIJA=@OLE('ss3','asa');!将文件名为'sab',名称为'asa'的数据块传递给SIJA; SIJB=@OLE('ss3','asb');!将文件名为'sab',名称为'asb'的数据块传递给SIJB; SIJC=@OLE('ss3','asc');!将文件名为'sab',名称为'asc'的数据块传递给SIJC; @OLE('ss3','axan')=X;!将Lingo的运行结果传递给Excel文件中名称为'axan'数据块; enddata min=@sum(Supply:X); @for(Week(j): 5/3*@sum(supply(i):XIJA(i,j))+50/33*@sum(supply(i):XIJB(i,j))+25/18*@sum(supply(i):XIJC(i,j))>=28200*0.99);!每周的产能约束; @for(Link(i,j):XIJA<=SIJA);!A类原材料的供应能力限制; @for(Link(i,j):XIJB<=SIJB);!B类原材料的供应能力限制; @for(Link(i,j):XIJC<=SIJC); !C类原材料的供应能力限制; @for(Supply(i): @sum(Week(j):XIJA(i,j))+@sum(Week(j):XIJB(i,j))+@sum(Week(j):XIJC(i,j))<=100000*X(i)); !逻辑约束; @for(Supply:@bin(X)); !0-1变量限制; end |
附录 Ⅲ 数据
问题1中用评价模型选出来的27家供应商
表 13 利用LFRM模型确定的27个供应商表
|
供应商ID |
材料分类 |
损耗率 |
订货量 |
采购成本 |
时间 |
WRSR |
|
S384 |
C |
3 |
9 |
6 |
5 |
0.9233 |
|
S243 |
A |
7 |
8 |
6 |
9 |
0.8898 |
|
S145 |
A |
9 |
7 |
7 |
8 |
0.8513 |
|
S116 |
A |
5 |
8 |
3 |
7 |
0.8403 |
|
S181 |
A |
8 |
9 |
3 |
8 |
0.8392 |
|
S159 |
A |
9 |
8 |
8 |
4 |
0.8388 |
|
S138 |
B |
9 |
8 |
6 |
5 |
0.8369 |
|
S317 |
A |
9 |
9 |
7 |
1 |
0.8315 |
|
S150 |
A |
9 |
8 |
6 |
4 |
0.8243 |
|
S392 |
B |
7 |
9 |
8 |
7 |
0.8175 |
|
S064 |
A |
1 |
7 |
8 |
4 |
0.8057 |
|
S389 |
B |
4 |
7 |
9 |
7 |
0.8052 |
|
S020 |
C |
8 |
9 |
6 |
3 |
0.7983 |
|
S333 |
B |
9 |
5 |
6 |
9 |
0.7947 |
|
S297 |
C |
8 |
5 |
4 |
4 |
0.7943 |
|
S199 |
B |
7 |
9 |
6 |
6 |
0.7891 |
|
S120 |
B |
7 |
3 |
5 |
1 |
0.7874 |
|
S377 |
C |
9 |
4 |
9 |
9 |
0.7855 |
|
S027 |
A |
7 |
9 |
5 |
6 |
0.7807 |
|
S169 |
B |
8 |
8 |
3 |
6 |
0.7785 |
|
S253 |
C |
8 |
8 |
6 |
4 |
0.7766 |
|
S166 |
B |
9 |
5 |
7 |
1 |
0.7762 |
|
S048 |
B |
7 |
8 |
3 |
6 |
0.77 |
|
S073 |
B |
9 |
5 |
6 |
7 |
0.7686 |
|
S213 |
C |
7 |
9 |
3 |
6 |
0.7657 |
|
S076 |
C |
7 |
7 |
8 |
8 |
0.7641 |
|
S135 |
C |
9 |
5 |
9 |
5 |
0.7641 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号