全国大学生数学建模2021B题(部分公式未展示)
针对港珠澳大桥桥梁设计与安全策略的研究
摘要
本文针对港珠澳大桥桥梁设计与安全策略的研究,运用最优化方法、演绎推理法、专家调研(Delphi)法,分别建立了优化模型和综合评价模型,并采用迭代算法,求出最优解。
对于问题1,运用演绎推理法,将受力分析与运动学原理相结合,确定目标函数,对处于弯道行驶的汽车建立优化模型。首先收集港珠澳大桥各项数据及详细参数,其次对汽车进行受力分析,当汽车处于弯道时,会受到重力、支持力、发动机引力、地面摩擦力及风力,将风力分为两种情况:推力和阻力,根据牛顿第三运动定律建立运动方程,构建优化模型,最后运用迭代算法,利用MATLAB软件求出最优解,结果显示汽车弯道处行驶时最大速度为。
对于问题2,运用最优化算法建立台风风级与车速模型,根据两个约束条件来确定最终的汽车最大安全行驶速度:题中所给的汽车最大行驶速度和台风天气下车辆不发生侧翻的汽车最大行驶速度。根据汽车受到重力、支持力、车速限制等条件,对汽车的最大安全行驶速度建立出优化模型,利用MATLAB软件进行求解,可以得到:当台风等级为12时,最大安全速度为;当台风等级为13时,最大安全速度为;当台风等级为14时,最大安全速度为;当台风等级为15时,最大安全速度为;当台风等级为16时,最大安全速度为。同时绘制出在不同台风等级下汽车的最大安全行驶速度随台风级数的变化图像,结果表明随着台风风级的增加,车辆的最大安全速度在不断减小,最大安全速度与台风等级成负相关。
对于问题3,运用专家调研(Delphi)法对港珠澳大桥的通行能力进行分析,构建港珠澳大桥综合评价模型。首先构建评价指标体系,确定评级指标为汽车安全通行情况、气候情况、交通情况,其次对评价指标进行规范化处理,设立量化标尺将定性指标定量化,之后运用相对比较法计算各评价指标权重,最后运用秩和比排序确定对通行能力影响最大的因素为汽车安全通行情况。根据不同车辆在大桥上速度限制不同,得到在最大通行能力下,大型机动车通过大桥的时长为;非大型机动车通过大桥的时长为。
关键词:桥梁设计与安全策略,优化模型,综合评价模型,MATLAB
1.
问题的重述
1.1 问题的背景
众所周知,港珠澳大桥是中国交通史上技术最复杂,建设要求及标准最高的工程之一,也是世界上最长的跨海大桥,被英国《卫报》誉为“新世界七大奇迹”。习**也曾这样称赞它“港珠澳大桥是国家工程、国之重器,其建设创下多项世界之最,非常了不起,体现了一个国家逢山开路、遇水架桥的奋斗精神,体现了我国综合国力、自主创新能力,体现了勇创世界一流的民族志气。这是一座圆梦桥、同心桥、自信桥、复兴桥。大桥建成通车,进一步坚定了我们对中国特色社会主义的道路自信、理论自信、 制度自信、文化自信,充分说明社会主义是干出来的,新时代也是干出来的!”
港珠澳大桥东接香港,西接珠海、澳门,全程55公里,由桥梁,人工岛,隧道三部分组成,其中,岛隧工程是大桥的控制性工程,需要建设两座面积各十万平方米的人工岛和一条6.7公里的海底沉管隧道,实现桥梁与隧道的转换,是大桥建设技术最复杂,建设难度最大的部分,极具挑战性。珠澳大桥沉管隧道,是我国建设的第一座外海沉管隧道,也是世界上最长的公路沉管隧道和唯一的深埋沉管隧道。
1.2 问题的提出
要求我们搜集相关数据,建立数学模型研究以下三个问题:
问题1:港珠澳大桥开通后,两岸三地实现了陆上通行,考虑各地的习惯和传统(港澳开车靠左行驶而内地靠右行驶),通过转向立交桥实现双方车辆在交通习惯上的自然过渡,请您对汽车(总重量范围:1000kg—3000kg,下同)在转向立交桥弯道处的行驶速度进行建模,并给出在弯道处的汽车最大安全行驶速度。
问题2:假定最大台风不超过16级,汽车最大行驶速度是。考虑不同风向的台风天气情况下,请您给出在整座大桥主体上汽车最大安全行驶速度和台风级数的关系。
问题3:假定大桥主体工程全线设计通行最大速度为100km/h,考虑汽车安全通行、气候情况、交通事故处理、交通控制等因素,对港珠澳大桥的通行能力进行建模。并在最大通行能力下(不考虑交通事故出现),给出机动车通过大桥的时长。
2. 问题的分析
2.1 对问题1的分析
对于问题1,对弯道处汽车的最大安全行驶速度进行求解,由于汽车都能在转弯处自由过度,所以在分析时可忽略汽车出现打滑、侧翻和碰撞等现象。在汽车转弯的过程中,从垂直和水平两个方向对汽车进行受力分析,汽车受到重力、支持力、发动机的牵引力、地面的摩擦力及风力。之后从运动学原理出发去分析汽车的运动状态,建立出汽车的目标函数。
汽车在弯道处行驶时,考虑三个方面的因素,分别为:弯道、风、车。首先,弯道一定是弧线,可以看成是圆周运动的一部分;其次,风对汽车的作用力可能是推力,也可能是阻力,在对汽车进行受力分析时需要分成两种情况;最后,车的质量在1000kg-3000kg之间,为简化运算可以将汽车看成质点。之后,进行资料的查找和相关文献的搜索,选择与速度有必然联系的优化模型。最后,正确的建立出合适的求解模型,求出弯道处汽车最大安全行驶速度。
2.2 对问题2的分析
对于问题2,由于汽车在行驶过程中会受到侧风作用,侧风的风速、风向角与车速都会对汽车的稳定性产生不同程度的影响,要得到大桥上汽车最大安全行驶速度和台风级数的关系,首先就要确保汽车在行驶过程中的稳定性,即通过计算风速和风向对汽车的稳定性进行建模。预计从两个方面确定最终的汽车最大安全行驶速度的约束条件:题中所给的汽车最大行驶速度和台风天气下车辆不发生侧翻的汽车最大行驶速度。
其次,需要考虑不同风向的台风天气对汽车行驶产生的影响。根据题目中所给的参考资料可以看出,台风的级数是12-16级,不同等级的台风风速不同,经过上网查找资料和查阅相关文献,决定选取不同等级台风的风速均值进行计算,使问题变的更加清晰明了。之后,从多个角度,如汽车受到的压强、重力、支持力、车速限制等,对汽车的最大安全行驶速度建立优化模型。最后,得出一个关于汽车的最大安全行驶速度与台风级数的目标函数,利用MATLAB软件进行求解,绘制出在不同台风等级下汽车的最大安全行驶速度随台风级数的变化图像,得到汽车最大安全行驶速度与台风级数的关系。
2.3 对问题3的分析
对于问题3,要根据汽车安全通行、气候情况、交通事故处理、交通控制等因素,对港珠澳大桥的通行能力进行建模。首先采用专家调研法(Delphi)征求16位专家的意见,将影响港珠澳大桥通行能力的主要因素可以归结为三种:汽车安全通行情况、气候情况、交通情况。
由于综合评价模型是一种对多属性(或多指标)的评价模型,而且能够对被评价对象进行的客观、公正、合理的全面评价,预计利用以上三种情况对港珠澳大桥通行能力建立综合评价模型。在构建评价指标体系时要注意两点:首先是查阅相关资料,筛选出合理的指标体系;其次是指标不要太直白,要让指标显示的更为高端。评价指标不能太少,否则不具备代表性,此外,奇数个评价指标更方便对指标进行分类,所以评价指标可以设为5个:影响较大、影响大、影响一般、影响小、影响较小。之后按照综合评价模型的建立步骤:构建评价指标体系、评价指标规范化处理、评价指标权重系数的确定、构建综合评价模型,完成建模。其中,确定各个指标的权重时可以借助MATLAB软件。求出对港珠澳大桥的通行能力影响最大的因素,最后结合汽车的优化模型计算出机动车通过大桥的时长。
3. 模型的假设
针对所给问题,考虑各种因素对建模的影响,给出如下假设:
- 忽略汽车轮胎结构、花纹、材料及港珠澳大桥的粗糙程度对摩擦因数的影响;
- 假设汽车在弯道行驶时不发生侧滑、侧翻、碰撞等现象;
- 假设问题3中不出现冰雹、疫情、大雪天气等自然灾害;
4. 符号说明
表 1 符号说明表
|
符号 |
说明 |
单位 |
|
汽车受到的支持力 |
||
|
发动机的牵引力 |
||
|
路面对汽车的摩擦力 |
||
|
风对汽车的阻(推)力 |
||
|
车辆行驶方向与风向的夹角 |
度 |
|
|
顺(逆)风转弯时达到的最大安全速度 |
||
|
汽车转弯时达到的最大安全速度 |
||
|
汽车顺(逆)风转弯时耗费的时间 |
||
|
弧线(弯道)长度 |
||
|
汽车转弯时的向心加速度 |
||
|
汽车转弯时的整体速度 |
||
|
汽车转弯时的整体(侧向)加速度 |
||
|
风速与车速的矢量和 |
||
|
汽车底面的面积 |
||
|
风速 |
||
|
车辆在台风下的行驶速度 |
||
|
个评价对象 |
- |
|
|
个评价指标 |
- |
|
|
指标可能取值的最大值 |
- |
|
|
评分矩阵 |
- |
|
|
秩矩阵 |
- |
5. 模型的建立与求解
5.1 问题1的建模与求解
对于问题1,考虑三个方面,分别为:桥、风、车。首先是从转向立交桥的角度来看,转向立交桥采用了“麻花”设计,让司机以“左上右落,右上左落”的方式行驶,当内地车辆开车上大桥时,依然按照内地的习惯靠右行驶;当车辆到达香港或者澳门口岸,即将下桥时,就会通过一座用于转向的立交桥,不用停车,不用换向,车辆自然而然地就从右车道变成了左车道。港珠澳大桥的转向立交桥设计如图1所示:

图1 转向立交桥的设计图
由上图可知:转向立交桥可以分成直线和弧线两部分。需要研究的是汽车在转向立交桥弯道处的最大安全行驶速度,则只需考虑弧线部分,即弯道处。
5.1.1确定决策变量及约束条件
将弯道看作圆周运动的一部分,汽车在弧线处行驶时,会受到重力、支持力、发动机的牵引力、路面对汽车的摩擦力及风对汽车的阻力或(推力)。其中,路面对汽车的摩擦力、发动机的牵引力及风对汽车的阻力(或推力)提供向心力;其次考虑风向,分为顺风、逆风和侧风三种。顺风时对汽车是推力,逆风时对汽车是阻力,侧风时可为推力,也可为阻力,侧风情况可归结到以上任意一种,因此,只考虑顺风和逆风两种情况。最后从汽车的角度出发,汽车的总重量范围在1000-3000kg之间,在建模过程中统称为,在受力分析的过程中,将汽车看作质点进行建模。
其决策变量即问题需要求解的未知量,即为、;
约束条件有两个:摩擦系数的取值范围为[1];风速与车速的夹角的取值范围为。
5.1.2确定目标函数并建立优化模型
根据以上分析,可以将问题1分为以下两种情况进行建模。顺风时汽车转弯过程中的受力分析图如图2所示:
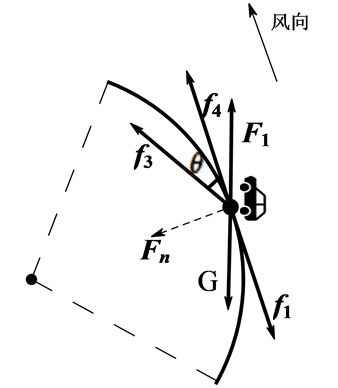
图 2 顺风时受力分析图
根据汽车受力情况,由牛顿第三运动定律即运动学原理得到目标函数如下
(1)
其中为车辆行驶方向与风向的夹角,为弧线(弯道)所在圆的半径, 为能够在此段弧线上顺风转弯时达到的最大安全速度,为汽车在此段弧线上行驶的向心加速度。
由决策变量、目标函数及其约束条件建立优化模型为
(2)
逆风时汽车转弯过程中的受力分析图如图3所示:
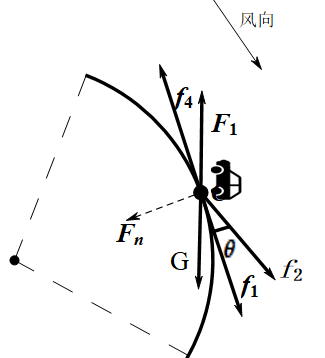
图 3 逆风时受力分析图
根据汽车受力情况,由牛顿第三运动定律及运动学原理得到目标函数如下
(3)
其中。 为能够在此段弧线(弯道)上逆风时转弯达到的最大安全速度,为车辆行驶方向与风向的夹角,为弧线所在圆的半径,为转向正交桥上截取的特定一段弧线(弯道)长度, 为汽车在此段弧线(弯道)上行驶的向心加速度, 为汽车逆风转弯时耗费的时间。
由决策变量、目标函数及其约束条件建立优化模型为
(4)
5.1.3确定的关系
在确定汽车转弯过程中的关系之前,对平曲线的速度模型进行调查,得出如表2所示的调查结果
表 2 针对平曲线模型的调查表
|
模型发布者 |
模型来源 |
表达式 |
|
Ottesen等 |
[2] |
注:
利用如下表达式,对汽车在转弯过程中的之间的关系进行建模
(5)
其中表示汽车转弯时的速度。
利用MATLAB求解(程序见附录)可得与的关系如图4所示:
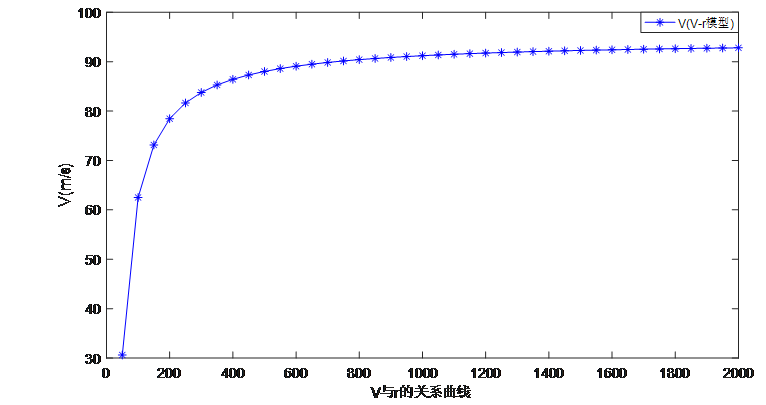
图4 汽车转弯速度与弧线半径的关系图
从图中,我们可以得到结论:汽车转弯时的速度随r的增大而增大。结合公式(2)、公式(4)中转弯时加速度与速度的关系,将图2运用MATLAB软件(程序见附录)进行变换,得到与的关系曲线如图5所示:
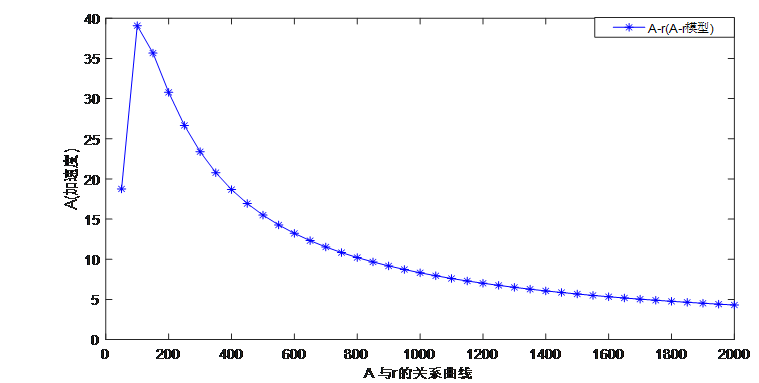
图 5 汽车转弯加速度与弧线半径的关系图
从图中,我们可以得到结论:汽车转弯时的加速度随的增加而递减。由于回归分析可以准确地计量各个因素之间的相关程度与回归拟合程度的高低。考虑到汽车行驶速度与弧线半径的关系,汽车加速度与弧线半径的关系,将与的关系曲线进行离散化处理,并对得到的数据进行回归分析,可以得到以为自变量的侧向加速度的侧向加速度回归模型[6]
(6)
回归分析后的用MATLAB拟合(程序见附录),拟合结果如图6所示:
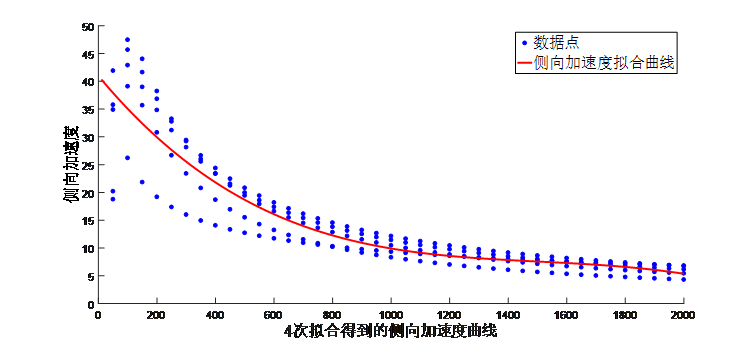
图 6 侧向加速度拟合曲线图
5.1.4优化模型的求解
对港珠澳大桥进行研究,可以得到以下数据:港珠澳大桥全长55千米,其中珠澳口岸至香港口岸 41.6干米,跨海路段全长35.578千米;三地共建主体工程29.6千米,包括7.2千米海底隧道和22.4千米主桥桥梁;江海航道桥的弯道半径介于600-1000米[8],选取江海航道桥的弯道为数据来源。
由侧向加速度与弧线半径的关系、速度与半径的关系,利用公式(6)可以得到速度与侧向加速度的关系:
(7)
将弯道半径区间代入公式(7),可以得到最大安全速度所在区间为:
即弯道处的汽车最大安全行驶速度为。
5.2问题2的建模与求解
汽车在行驶过程中会受到侧风作用,侧风的风速、风向角与车速都会对汽车的稳定性产生不同程度的影响,要得到整座大桥主体上汽车最大安全行驶速度和台风级数的关系,首先就要确保汽车在行驶过程中的稳定性,即可以通过研究风速和风向对汽车的稳定性进行建模。汽车在行驶过程中的模拟图像如图7所示
图 7 汽车行驶模拟图
5.2.1确定决策变量及约束条件
其决策变量为问题需要求解的未知量,即为整座大桥主体上汽车最大安全行驶速度,此处为风速和车速的矢量和;由于汽车要正常行驶,因此向上的支持力不能大于汽车的重力,根据题意,汽车的最大车速不得超过,因此问题2共存在两个约束条件,分别为:
5.2.2确定目标函数并建立优化模型
根据题目给出的参考资料可以得到,不同等级台风的风速是不同的,为了简化运算,这里取不同等级的台风的风速均值进行计算,设风速为,汽车在台风下的行驶速度为,风速与车速的矢量和为,风速与车速的夹角设为,由余弦定理可得:
(8)
则其目标函数为:
(9)
由决策变量、目标函数及其约束条件建立优化模型为
(10)
将汽车在不同的速度下受到的压强设为,空气密度设为,查阅相关资料后可以得到,由此可以确定汽车单位面积所受到的压强:
(11)
对汽车进行竖直方向上的受力分析,可以得到:汽车受到向上的支持力和向下的重力,设向上的支持力为,向下的重力为,汽车底面的面积为,质量设为,重力加速度为,则汽车的所受到的支持力和重力分别为:
(12)
(13)
5.2.3优化模型的求解
Step1:所给定的汽车的质量,取质量均值,令;
Step2:取等不同的角度;
Step3:汽车的质量均值和所取的不同角度带入模型进行计算求出不同台风等级和风向下所对应的最大车速,利用MATLAB绘制出不同台风等级下汽车最大安全行驶速度随风向的变化图(程序见附录)如图8、图9、图10、图11所示
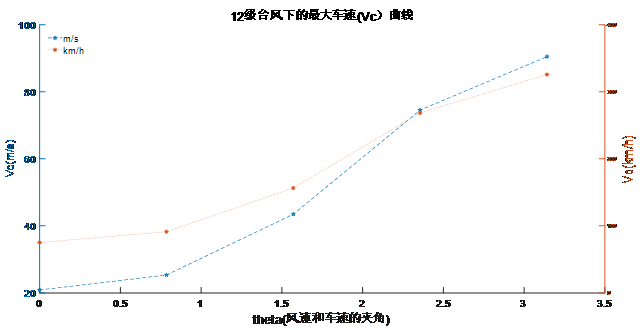
图 8 12级台风下最大安全车速随风向的变化图
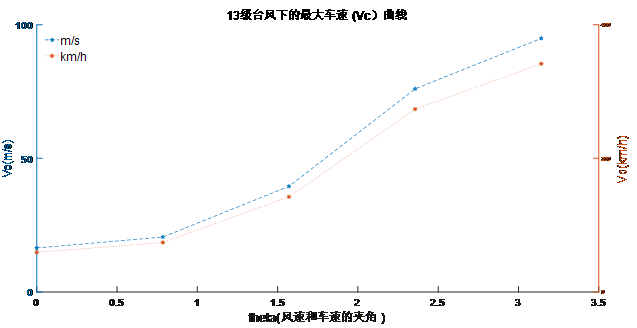
图 9 13级台风下最大安全车速随风向的变化图
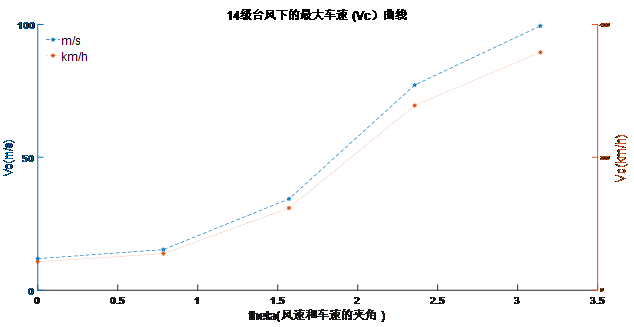
图 10 14级台风下最大安全车速随风向的变化图
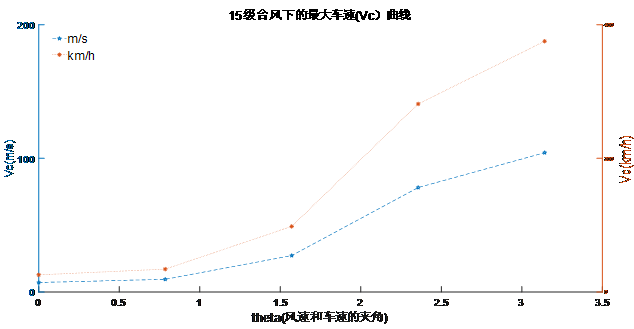
图 11 15级台风下最大安全车速随风向的变化图
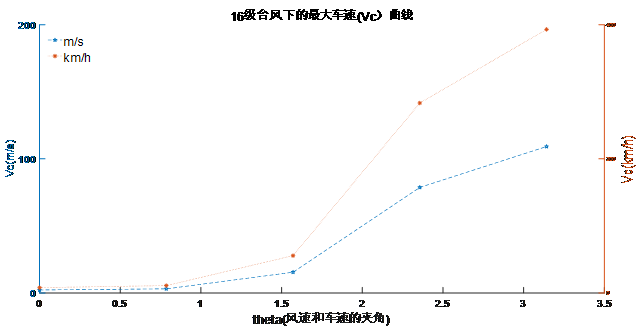
图 12 16级台风下最大安全车速随风向的变化图
Step4:利用MATLAB软件绘制出汽车最大安全行驶速度和台风级数的关系图(程序见附录)如图13所示。
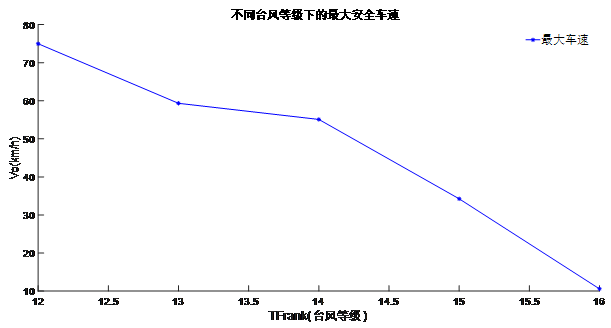
图 13 最大安全车速与台风等级间的关系图
由此可知随着台风风级的增加,车辆的最大安全速度在不断减小,最大安全速度与台风等级成负相关。
5.2.4求解结果
按照以上步骤依次进行,最后可以得出,在整座大桥主体上汽车最大安全行驶速度和台风级数的关系。整理后得到最终的求解结果图如表3所示
表 3 求解结果图
|
风级 |
车速() |
车速() |
|
12 |
20.83 |
74.97 |
|
13 |
16.48 |
59.34 |
|
14 |
15.31 |
55.12 |
|
15 |
9.51 |
34.25 |
|
16 |
2.95 |
10.62 |
由此可知当台风等级为12时,最大安全速度为;当台风等级为13时,最大安全速度为;当台风等级为14时,最大安全速度为;当台风等级为12时,最大安全速度为;当台风等级为12时,最大安全速度为。
5.3问题3的建模与求解
5.3.1构建评价指标体系
影响港珠澳大桥通行能力的因素有很多,如汽车安全通行、气候情况、交通事故处理、交通控制等因素,为了合理地选取主要指标,剔除次要指标,简化评价指标体系,采用专家调研法(Delphi)进行指标的筛选。其流程见图14:

图 14 Delphi法流程图
通过专家调研法对指标进行筛选,最终确定评价对象有3个:汽车安全通行情况、气候情况、交通情况。分别记为
其中极大型指标为汽车安全通行情况;中间型指标为气候情况;极小型指标为交通情况。每个评价对象均有5个指标:影响较大、影响大、影响一般、影响小、影响较小,分别记为:
5.3.2评价指标规范化处理
一般情况下,在综合评价指标中,各指标可能属于不同类型、不同单位、不同数量级,从而使得各指标之间存在着不可公度性,给综合评价带来了诸多不便。为了尽可能地反映实际情况,消除由于各项指标间的这些差别,避免出现不合理的评价结果,就需要对评价指标进行一定的规范化处理,其中规范化处理包括一致化、定性指标定量化、无量钢化。可以看出,该体系的指标大多都为定性指标,只给出定性描述,想要进一步深入研究,就要对其进行定量化处理,处理的具体准则见图15所示:

图 15 量化标尺
结合图5,可以将定性指标转化为定量指标,将转化为具体数值,可以采用1-9比例标度法来度量各个指标,标度及其含义如下表所示:
表 4 1-9比例标度值
|
标度 |
含义 |
|
1 |
与的影响相同 |
|
3 |
比的影响稍强 |
|
5 |
比的影响强 |
|
7 |
比的影响明显的强 |
|
9 |
比的影响绝对的强 |
|
2,4,6,8 |
与的影响之比介于上述两个相邻等级之间 |
|
与的影响之比为上面影响的倒数 |
其中,
可以将5个指标分别记为
采用将极小型指标转化为极大型指标的方式进行一致性处理,将评价指标全部转换为极大型。通过变换
(14)
得到经过一致性处理的关系矩阵
在实际评价中,各个指标会存在不同的单位和数量级,这些问题的存在会使得在综合评价中出现“大数吃小数”情况,为了避免这种情况的出现,使综合评价法做到最优,需对各指标进行无量纲化处理,本次采用的处理方法为极值差法,利用公式
(15)
其中经过(15)式的处理后得到矩阵
5.3.3评价指标权重系数的确定
在综合评价指标中,想要得到科学、公正、合理的评价结果,就必须考虑各项指标对总体目标实现的重要程度,即评价指标的权重系数。确定指标的权重系数的方法一共有三种,分别为主观赋权法、客观赋权法、综合集成赋权法。根据对这三种方法的掌握程度,本文选择使用主观赋权法中的相对比较法确定权重。
三级指标两两比较评分的分值为,标度值及其含义如下
(16)
则评分矩阵,显然,,则第项指标为的权重为
(17)
根据公式(17)确定权重为
5.3.4构建综合评价模型
综合评价模型就是将同一评价对象不同方面的多个指标综合在一起,得到一个整体性评价指标值。综合评价模型的类型有三种,分别是简单加权综合模型、逼近理想解法、秩和比法。因秩和比法具有参数选择无特殊要求,适用于各种评价对象,可消除异常值的干扰等优点,所以选取秩和比(RSR)法。该方法的基本原理是在一个行列矩阵中,通过秩转换,获得无量纲统计量RSR,运用参数统计分析的概念与方法,研究RSR的分布以及RSR对评价对象的优劣排序,从而对评价对象做出综合评价。
(1) 编秩
将个评价对象个评价指标排列成行列的原始数据表,根据效益性指标从小到大编秩,成本型指标从大到小编秩的原则,得出秩矩阵
(2) 计算秩和比
如果各评价指标权重相同,可用公式(18)计算秩和比;若各个指标权重不相同,则用公式(19)计算加权秩和比
(18)
(19)
其中:为第个评价指标的权重,。
由于上文求出的权重皆不相同,所以选取公式(12)进行计算求出秩和比为:
(3) 秩和比排序
根据对评价对象进行排序可得0.523>0.408>0.33,结果表明,对港珠澳大桥的通行能力影响较大的因素是汽车安全通行情况。
之后考虑对速度的影响,对于大型汽车而言,在主桥行驶时需要使用慢线,其车速限制为。港珠澳大桥全长55千米,主桥长度为。根据汽车的总重量范围(1000-3000kg)可以分两部分考虑:大型车辆和普通车辆。结合汽车优化模型中的公式(2)和公式(4),大型机动车通过大桥的时长为限速时段所花费的时间与非限速阶段所花费的时间之和,即
(20)
对于非大型机动车而言,由于大桥主体工程全线设计通行最大速度为,但在汽车行驶的过程中,由于汽车安全通行情况和交通情况二者的秩和比相差不大,所以还需要着重考虑汽车安全通行情况和交通情况,结合汽车运动模型中的公式(2)和公式(4)可求出非大型机动车通过大桥的时长为
(21)
6. 模型的检验
6.1 问题1模型的检验
对于问题1,采用结果对比的方法,将优化模型得到的最优解与所建立的平曲线模型得到的结果进行比较,若求出的汽车最大安全行驶速度相近或相等,就认为求解正确。
从物理学的角度分析,汽车受到的重力、支持力、发动机的牵引力、路面对汽车的摩擦力及风对汽车的阻力(或推力)。其中,路面对汽车的摩擦力、发动机的牵引力及风对汽车的阻力(或推力)提供向心力。在进行检验时,可以将车辆行驶方向与风向的夹角看作0,即完全由摩擦力提供汽车在转弯时的向心力。据公式(1)和公式(3)可以得到
(22)
将公式(6)与公式(22)进行比较,可以得到公式(22)的运算结果稍大于公式(6)的运算结果,由此可以看出,通过物理分析得到的速度和通过平曲线模型得到的速度在本质上是一致的。所以,问题1所建的侧向加速度模型具有一定的可靠性。
6.2 问题2模型的检验
对于问题2,采用BP神经网络来进行验证,其输入层为风向、风速,输出层为整座大桥主体上汽车最大安全行驶速度,取风向为,风速取值按照台风等级选取12-16级的风速,分别取(这五个取值是按照题目中所给参考资料的风速范围得到的)。
用表示输入向量,表示输出向量;用分别表示输入层与隐藏层,隐藏层与输出层的连接权值;用分别表示隐藏层、输出层与各神经元阈值。隐藏层输出、输出层输出分别由以下两个公式得到
(23)
(24)
之后计算网络误差,进行权值和阈值的更新,通过算法迭代进行判断,若未结束就从隐藏层的输出继续进行。最后利用MATLAB处理可以绘制出如图16所示图像
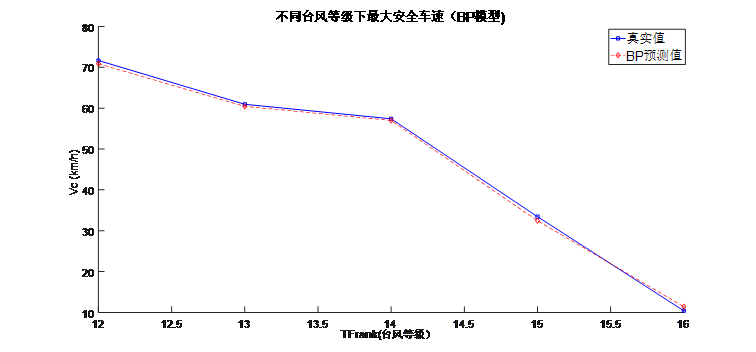
图 16 最大安全车速与台风等级间的关系图
根据绘制的图像可以看出,该图像与图13中所得到的图像几乎是相同的,可以得出问题2的建模也是十分合理。
6.3 问题3模型的检验
对于问题3,采用层次分析法进行检验,若由层次分析法得到的结果和所建立的综合评价模型得到的结果相近或相等,就认为求解正确。
从层次分析法来看,目标层是汽车的通行能力,一级指标是汽车安全通行情况、气候情况、交通情况,采用1-9比例标度来度量指标层的各个因素,构造层次判断矩阵
之后求出判断矩阵的最大特征值,对最大特征值对应的特征向量进行归一化处理,得到权重向量,接着进行层次排序及一致性检验,为了衡量的大小,引入随机一致性指标,与判断矩阵的阶数有关,对于不同的阶数 ,的值如表3所示
表 5 随机一致性指标的数值
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
0 |
0 |
0.58 |
0.9 |
1.12 |
1.24 |
1.32 |
1.41 |
1.45 |
1.49 |
1.51 |
由于计算所得的,则该判断矩阵通过一致性检验,具有满意一致性。最后利用MATLAB软件(程序见附录)进行求解,得到权重
根据权重可以得到结论:对港珠澳大桥的通行能力影响较大的因素是汽车安全通行情况。与综合评价模型得到的结论是一致的,所以问题3所建的综合评价模型具有一定的可靠性。
7. 模型的评价与推广
7.1 模型的评价
优化模型
优点:可以根据其决策变量、目标函数、约束条件得到最优解,求解准确。本文将汽车看作质点进行研究,从垂直和水平两个方面进行受力分析,将汽车的受力分析与运动情况联系起来,得到目标函数,利用MATLAB进行求解。
缺点:受实际条件限制,可能会使问题的处理发生较大的偏差;较其他模型而言,效率较低。
综合评价模型
优点:可以通过精确的数字手段处理评价对象,能对蕴藏信息作出科学、合理、贴近实际的量化评价;包含的信息比较丰富,既可以比较准确的刻画被评价对象,又可以进一步加工,得到参考信息;本文采用该方法找出了对港珠澳大桥通行能力影响最大的因素,将定性指标转化为定量指标,按照秩和比得到了一个相对优劣比的排序,得到了对港珠澳大桥通行能力影响程度的准确数值。
缺点:计算复杂,对指标权重矢量的确定主观性较强;
7.2 模型的推广
优化模型:优化模型应用领域十分广泛,如天体运动、自由落体运动、匀加速运动、变加速运动等都需要建立物理模型去解决。
综合评价模型:综合评价模型的应用领域非常广泛,可以推广到各种事物特征和性质的评价中,如小康建设进程的评价、药物临床试验的综合评价等。
8. 参考文献
[1] 孙应渝,吴宗兴.路面摩擦系数标准问题的研究[J].交通科技与经济,2017,10(5):54-56.
[2] MEMON R A, KHASKHELI G B,QURESHI A s.Operating Speed Models for Two-lane Rural Roads inPakistan[J.Canadian Journal of CivilEngineering,2008,35(5):443-453.
[3] 金智林.运动型多功能汽车侧翻稳定性及防侧翻控制[D].南京:南京航空航天大学,2018.
[4] Shuichi Takano S, et al. Study on vehicle dynamica model for improving roll stability[J.JSAE Review ,2003,24:149~156
[5] RICHL L,SAYED T.Effect of Speed Prediction Modelsand Perceived Radius on Design Consistency[J].Ca-nadian Journal of CivilEngineering,2005,32(2):388-399.
[6] 范振宇,张剑飞.公路运行车速测算模型的研究和标定[J].中国公路学报,2002(01):110-112.
[7] 韩中庚,陆宜清,周素静.数学建模实用教程[M].北京:高等教育出版社,2013. 200-207.
[8] 宋安,刘琦. 出租车保有量评价与预测[J].交通科技与经济,2010.12(3):34-36.
[9] 王明亮.关于中国学术期刊标准化数据库系统工程的进展[EB/OL]. [10]https://wenku.baidu.com/view/f1eb312bcc2f0066f5335a8102d276a20129608d.html,2021-07-23.
[10]杨俊儒,褚端峰,王维锋,万剑,邓泽健,吴超仲.弯道安全车速建模及影响因素分析[J].交通信息与安全,2018,36(06):1-8.
附录
附录 问题1中与的关系图程序
|
r=0:50:2000; V1=94.398-3188.656./r;%模型1 V3=95.594-1.597*1746.38./r;%模型3 V6=103.66-1.95*1746.38./r;%模板6 V7=129.88-623.10./ power(r,0.5);%模板7 V9=105.98-3709.90./r;%模板9 V13=115./(1+75.6375./r);%模板13 V14=14.391.*power(r,0.2755);%模板14 plot(r,V1,'b-*');hold on plot (r,V3,'g-o');hold on plot(r,V6,'r-h') ;hold on plot(r,V7,'c-+');hold on plot(r, V9,'m-*') ;hold on plot(r,V13,'y-d');hold on plot(r,V14,'k-p') ;hold on xlabel('V与r的关系曲线') ylabel('V(km/h)') legend('V1(模板1)','V3(模板3)', 'V6(模板6)', 'V7(模板7)', 'V9(模板9)','V13(模板13)','V14(模板14)'); |
附录 问题1中变换后与的关系图程序
|
%%% 问题1中与的关系图程序 r=0:50:2000;%A=V^2/R A1=power(94.398-3188.656./r,2)./r;%模板1 A7=power(129.88-623.10./power(r,0.5),2)./r;%模板7 A9=power(105.98-3709.90./r,2)./r;%模板9 A13=power(115./(1+75.6375./r),2)./r;%模板13 A14=power(14.391.*power(r,0.2755),2)./r;%模板14 plot(r,A1,'b-*');hold on plot(r,A7,'c-+');hold on plot(r,A9,'m-*');hold on plot(r,A13,'y-d');hold on plot(r,A14,'k-p');hold on xlabel('A与r的关系曲线') ylabel('A(加速度)') legend('A1(模板1)','A7(模板7)','A9(模板9)','A13(模板13)','A14(模板14)'); hold on plot(r,A7,'c-+');hold on plot(r, A9,'m-*');hold on plot(r,A13,'y-d');hold on plot(r,A14,'k-p');hold on |
附录 问题1中侧向加速度拟合曲线图程序
|
r=0:50:2000;%A=V^2/R A1=power(94.398-3188.656./r,2)./r;%模型1 A7=power(129.88-623.10./power(r,0.5),2)./r;%模型7 A9=power(105.98-3709.90./r,2)./r;%模型9 A13=power(115./(1+75.6375./r),2)./r;%模型13 A14=power(14.391.*power(r,0.2755),2)./r;%模型14 r=[r,r,r,r,r]; A=[A1,A7,A9,A13,A14] ; plot(r,A, 'bo','MarkerFaceColor', 'b'); xlabe1('4次拟合得到的侧向加速度曲线'); ylabel('侧向加速度') ; hold on x=10:1:2000; fx=5.857e-13*x.^4-1.127e-08*x.^3+4.296e-05*x.^2-0.06332*x+40.96; plot(x,fx,'r-', 'linewidth', 3); legend('数据点','侧向加速度拟合曲线'); cftool; |
附录 问题2中安全行驶车速与风向变化图程序
|
clc;clear; %台风风级为12时的最大安全车速 syms Vc global MaxSafeVc_ms_12 global MaxSafeVc_kmh_12 Vf=53.5; M=2000; g=10; G=M*g; S=10;
thetal=0; theta2=pi/4; theta3=pi/2; theta4=3*pi/4; theta5=pi;
V1=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-thetal)); P1=(1.29*V1^2)/2; F1=P1*S; eq1=F1-G; s1=max(solve(eq1,Vc));
V2=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta2)); P2=(1.29*V2^2)/2; F2=P2*S; eq2=F2-G; s2=max(solve(eq2,Vc));
V3=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta3)); P3=(1.29*V3^2)/2; F3=P3*S; eq3=F3-G; s3=max(solve(eq3,Vc));
V4=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta4)); P4=(1.29*V4^2)/2; F4=P4*S; eq4=F4-G; s4=max(solve(eq4,Vc));
V5=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta5)); P5=(1.29*V5^2)/2; F5=P5*S; eq5=F5-G; s5=max(solve(eq5,Vc));
sm=[s1,s2,s3,s4,s5]; skm=sm*3.6; V=100/3.6-sm; index=find(V==min(V(find(V>0)))); vpa(sm,4); MaxSafeVc_ms_12=vpa(sm(index),4) vpa(skm,4); MaxSafevc_kmh_12=vpa(sm(index)*3.6,4) theta=[thetal,theta2,theta3,theta4,theta5]; [AX,H1,H2] =plotyy(theta,sm,theta,skm,@plot);%获取坐标轴、图像句柄 set(get(AX(1),'ylabel'),'string','Vc(m/s)','fontsize',20); set(get(AX(2),'ylabel'),'string','Vc(km/h)','fontsize',20); xlabel('theta(风速和车速的夹角)','fontsize',20); set(H1,'Linestyle','--') ; set(H2,'Linestyle',':'); set(gcf,'color','white') set(gca,'linewidth',1.5) %设置边框宽度 legend('m/s','km/h'); title('12级台风下的最大车速(Vc)曲线','fontsize',20)
clc;clear; %台风风级为13时的最大安全车速 syms Vc global MaxSafeVc_ms_13 global MaxSafeVc_kmh_13 Vf=39.2; M=2000; g=10; G=M*g; S=10;
thetal=0; theta2=pi/4; theta3=pi/2; theta4=3*pi/4; theta5=pi;
V1=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-thetal)); P1=(1.29*V1^2)/2; F1=P1*S; eq1=F1-G; s1=max(solve(eq1,Vc));
V2=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta2)); P2=(1.29*V2^2)/2; F2=P2*S; eq2=F2-G; s2=max(solve(eq2,Vc));
V3=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta3)); P3=(1.29*V3^2)/2; F3=P3*S; eq3=F3-G; s3=max(solve(eq3,Vc));
V4=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta4)); P4=(1.29*V4^2)/2; F4=P4*S; eq4=F4-G; s4=max(solve(eq4,Vc));
V5=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta5)); P5=(1.29*V5^2)/2; F5=P5*S; eq5=F5-G; s5=max(solve(eq5,Vc));
sm=[s1,s2,s3,s4,s5]; skm=sm*3.6; V=100/3.6-sm; index=find(V==min(V(find(V>0)))); vpa(sm,4); MaxSafeVc_ms_13=vpa(sm(index),4)
vpa(skm,4); MaxSafevc_kmh_13=vpa(sm(index)*3.6,4) theta=[thetal,theta2,theta3,theta4,theta5]; [AX,H1,H2] =plotyy(theta,sm,theta,skm,@plot);%获取坐标轴、图像句柄 set(get(AX(1),'ylabel'),'string','Vc(m/s)','fontsize',20); set(get(AX(2),'ylabel'),'string','Vc(km/h)','fontsize',20); xlabel('theta(风速和车速的夹角)','fontsize',20); set(H1,'Linestyle','--') ; set(H2,'Linestyle',':'); set(gcf,'color','white') set(gca,'linewidth',1.5) %设置边框宽度 legend('m/s','km/h'); title('13级台风下的最大车速(Vc)曲线','fontsize',20)
clc;clear; %台风风级为14时的最大安全车速 syms Vc global MaxSafeVc_ms_14 global MaxSafeVc_kmh_14 Vf=43.8; M=2000; g=10; G=M*g; S=10;
thetal=0; theta2=pi/4; theta3=pi/2; theta4=3*pi/4; theta5=pi;
V1=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-thetal)); P1=(1.29*V1^2)/2; F1=P1*S; eq1=F1-G; s1=max(solve(eq1,Vc));
V2=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta2)); P2=(1.29*V2^2)/2; F2=P2*S; eq2=F2-G; s2=max(solve(eq2,Vc));
V3=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta3)); P3=(1.29*V3^2)/2; F3=P3*S; eq3=F3-G; s3=max(solve(eq3,Vc));
V4=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta4)); P4=(1.29*V4^2)/2; F4=P4*S; eq4=F4-G; s4=max(solve(eq4,Vc));
V5=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta5)); P5=(1.29*V5^2)/2; F5=P5*S; eq5=F5-G; s5=max(solve(eq5,Vc));
sm=[s1,s2,s3,s4,s5]; skm=sm*3.6; V=100/3.6-sm; index=find(V==min(V(find(V>0)))); vpa(sm,4); MaxSafeVc_ms_14=vpa(sm(index),4)
vpa(skm,4); MaxSafevc_kmh_14=vpa(sm(index)*3.6,4) theta=[thetal,theta2,theta3,theta4,theta5]; [AX,H1,H2] =plotyy(theta,sm,theta,skm,@plot);%获取坐标轴、图像句柄 set(get(AX(1),'ylabel'),'string','Vc(m/s)','fontsize',20); set(get(AX(2),'ylabel'),'string','Vc(km/h)','fontsize',20); xlabel('theta(风速和车速的夹角)','fontsize',20); set(H1,'Linestyle','--') ; set(H2,'Linestyle',':'); set(gcf,'color','white') set(gca,'linewidth',1.5) %设置边框宽度 legend('m/s','km/h'); title('14级台风下的最大车速(Vc)曲线','fontsize',20)
clc;clear; %台风风级为15时的最大安全车速 syms Vc global MaxSafeVc_ms_15 global MaxSafeVc_kmh_15 Vf=48.55; M=2000; g=10; G=M*g; S=10;
thetal=0; theta2=pi/4; theta3=pi/2; theta4=3*pi/4; theta5=pi;
V1=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-thetal)); P1=(1.29*V1^2)/2; F1=P1*S; eq1=F1-G; s1=max(solve(eq1,Vc));
V2=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta2)); P2=(1.29*V2^2)/2; F2=P2*S; eq2=F2-G; s2=max(solve(eq2,Vc));
V3=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta3)); P3=(1.29*V3^2)/2; F3=P3*S; eq3=F3-G; s3=max(solve(eq3,Vc));
V4=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta4)); P4=(1.29*V4^2)/2; F4=P4*S; eq4=F4-G; s4=max(solve(eq4,Vc));
V5=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta5)); P5=(1.29*V5^2)/2; F5=P5*S; eq5=F5-G; s5=max(solve(eq5,Vc));
sm=[s1,s2,s3,s4,s5]; skm=sm*3.6; V=100/3.6-sm; index=find(V==min(V(find(V>0)))); vpa(sm,4); MaxSafeVc_ms_15=vpa(sm(index),4)
vpa(skm,4); MaxSafevc_kmh_15=vpa(sm(index)*3.6,4) theta=[thetal,theta2,theta3,theta4,theta5]; [AX,H1,H2] =plotyy(theta,sm,theta,skm,@plot);%获取坐标轴、图像句柄 set(get(AX(1),'ylabel'),'string','Vc(m/s)','fontsize',20); set(get(AX(2),'ylabel'),'string','Vc(km/h)','fontsize',20); xlabel('theta(风速和车速的夹角)','fontsize',20); set(H1,'Linestyle','--') ; set(H2,'Linestyle',':'); set(gcf,'color','white') set(gca,'linewidth',1.5) %设置边框宽度 legend('m/s','km/h'); title('15级台风下的最大车速(Vc)曲线','fontsize',20)
clc;clear; %台风风级为16时的最大安全车速 syms Vc global MaxSafeVc_ms_16 global MaxSafeVc_kmh_16 Vf=53.5; M=2000; g=10; G=M*g; S=10;
thetal=0; theta2=pi/4; theta3=pi/2; theta4=3*pi/4; theta5=pi;
V1=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-thetal)); P1=(1.29*V1^2)/2; F1=P1*S; eq1=F1-G; s1=max(solve(eq1,Vc));
V2=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta2)); P2=(1.29*V2^2)/2; F2=P2*S; eq2=F2-G; s2=max(solve(eq2,Vc));
V3=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta3)); P3=(1.29*V3^2)/2; F3=P3*S; eq3=F3-G; s3=max(solve(eq3,Vc));
V4=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta4)); P4=(1.29*V4^2)/2; F4=P4*S; eq4=F4-G; s4=max(solve(eq4,Vc));
V5=sqrt(Vc^2+Vf^2-2*Vc*Vf*cos(pi-theta5)); P5=(1.29*V5^2)/2; F5=P5*S; eq5=F5-G; s5=max(solve(eq5,Vc));
sm=[s1,s2,s3,s4,s5]; skm=sm*3.6; V=100/3.6-sm; index=find(V==min(V(find(V>0)))); vpa(sm,4); MaxSafeVc_ms_16=vpa(sm(index),4)
vpa(skm,4); MaxSafevc_kmh_16=vpa(sm(index)*3.6,4) theta=[thetal,theta2,theta3,theta4,theta5]; [AX,H1,H2] =plotyy(theta,sm,theta,skm,@plot);%获取坐标轴、图像句柄 set(get(AX(1),'ylabel'),'string','Vc(m/s)','fontsize',20); set(get(AX(2),'ylabel'),'string','Vc(km/h)','fontsize',20); xlabel('theta(风速和车速的夹角)','fontsize',20); set(H1,'Linestyle','--') ; set(H2,'Linestyle',':'); set(gcf,'color','white') set(gca,'linewidth',1.5) %设置边框宽度 legend('m/s','km/h'); title('16级台风下的最大车速(Vc)曲线','fontsize',20) |
附录 问题2中安全行驶车速与风向变化图程序
|
%最大安全车速与台风等级的关系 clc; TFrank=[12,13,14,15,16]; MostSafeVc_kmh=[74.9700,59.3400,55.1000,34.2500,10.6000]; plot(TFrank,MostSafeVc_kmh,'b-'); hold on; title('不同台风等级下的最大安全车速') xlabel('TFrank(台风等级)'); ylabel('Vc(km/h)'); legend('最大车速'); |
附录 问题3检验时层次分析法求权重程序
|
clc; clear; disp('请输入判断矩阵A'); %111111111 A=input('A='); [m,n]=size(A); %获取指标个数 RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; R=rank(A); %求判断矩阵的秩 [V,D]=eig(A); %求判断矩阵的特征值和特征向量,V特征值,D特征向量; tz=max(D); B=max(tz); %最大特征值 [row, col]=find(D==B); %最大特征值所在位置 C=V(:,col); %对应特征向量 CI=(B-n)/(n-1); %计算一致性检验指标CI CR=CI/RI(1,n); if CR<0.10 disp('CI=');disp(CI); disp('CR=');disp(CR); disp('对比矩阵A通过一致性检验,各向量权重向量Q为:'); Q=zeros(n,1); for i=1:n Q(i,1)=C(i,1)/sum(C(:,1)); %特征向量标准化 end Q %输出权重向量 else disp('对比矩阵A未通过一致性检验,需对对比矩阵A重新构造'); end |



