熵权（值）法计算权重原理解释&综合得分纵向对比
熵值是不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。因而利用熵值携带的信息进行权重计算，结合各项指标的变异程度，利用信息熵这个工具，计算出各项指标的权重，为多指标综合评价提供依据。
权重计算
熵值法的计算公式如下：
参考文献：[1]张晓捷.基于熵权TOPSIS法的长租公寓财务风险评价及防范研究[D].广西大学,2022.DOI:10.27034/d.cnki.ggxiu.2022.001712.
step1：
根据研究者的数据进行构建评价矩阵（其实就是整理好正确的数据格式，一行为一个样本，一列为一个属性）；
step2：
根据指标的属性进行数据处理，常用的为正向化处理和逆向化处理，有时财务数据还会进行适度化处理，适度化是指数据越接近某个值越好。
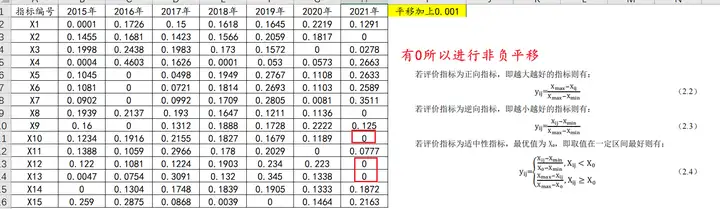
step3：非负处理
除此之外，还需要对step2的矩阵进行非负处理（仅针对数据中有非负数据，为什么进行处理呢？计算中有ln函数，不处理无法计算，可见下方计算公式），至于平移多少，不同的文献，处理不同，以参考的文献为准。常见的有0.0001、0.01、1等。此文献是平移0.001，不管平移多少，其目的最终都是为了数据满足熵值法的计算要求。
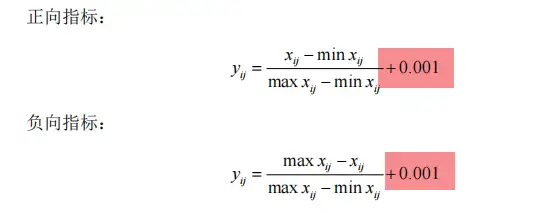
平移后的矩阵如下：
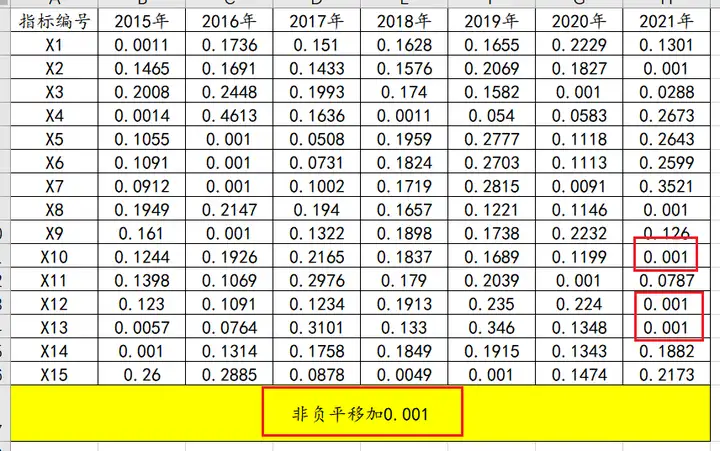
step4：
对非负处理后的矩阵进行归一化处理：
①列求和：
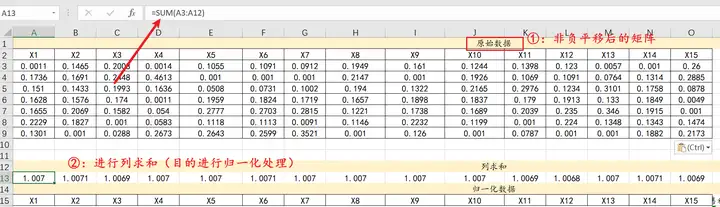
②归一化处理
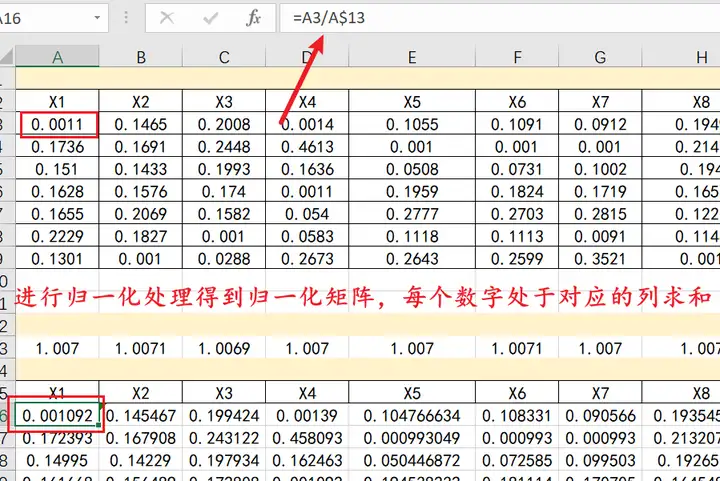
0.0011/1.007=0.001092;0.1465/1.0071=0.145467，以此类推；
step5：求1/ln（n）
有些文献还称1/ln(n)为k，所以在其他文献中看到熵值计算公式里的k其实就是1/ln(n)，其中n为样本量，也就是数据中的行数，有几行就除以几；
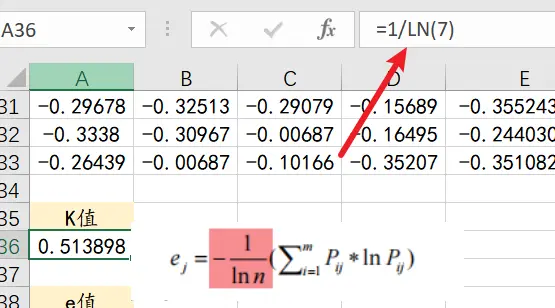
step6：求数据与对数乘积(p*lnp)
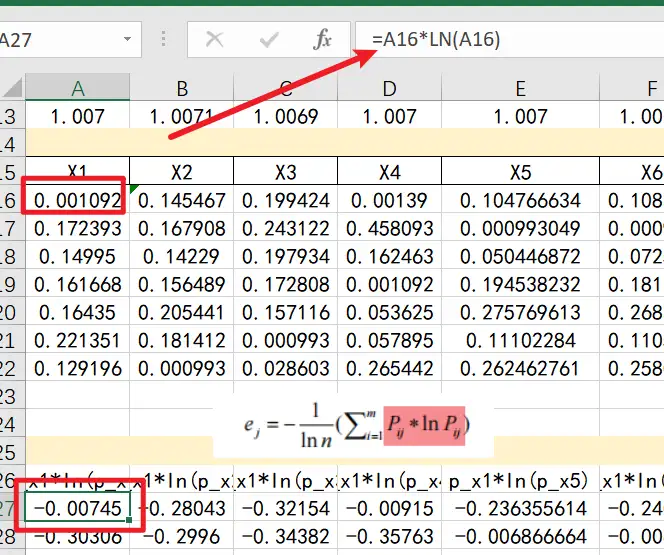
使用的是归一化后的数据，比如0.001092*ln（0.001092）=-0.00745;以此类推；
step7：求熵值
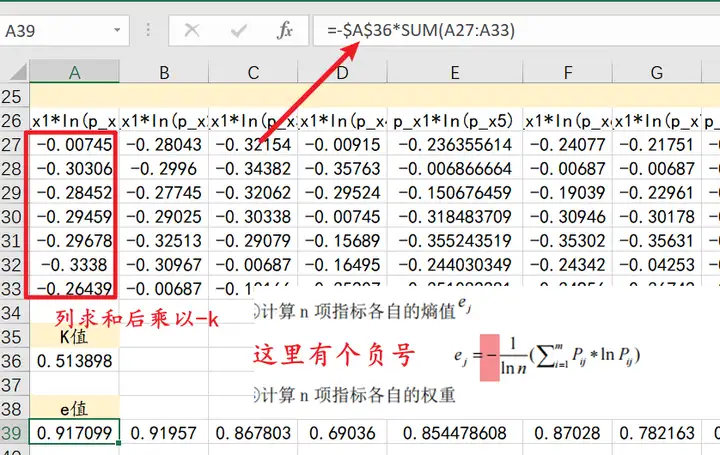
对数据与对数乘积矩阵每一列求和，求和后乘以-k就是对应的每一个属性的熵值；
step8：求差异系数
差异系数=1-熵值；
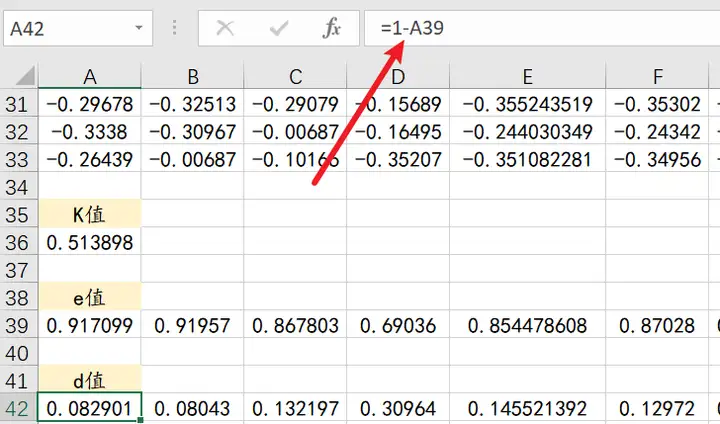
step9：求权重
对差异系数进行归一化处理；
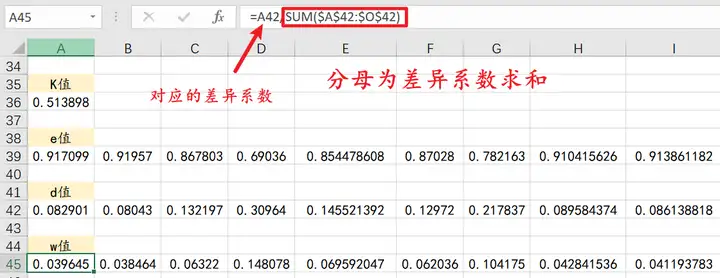
除此之外，也可以使用spssau进行分析，中间处理过程spssau会默认进行。
结果如下：
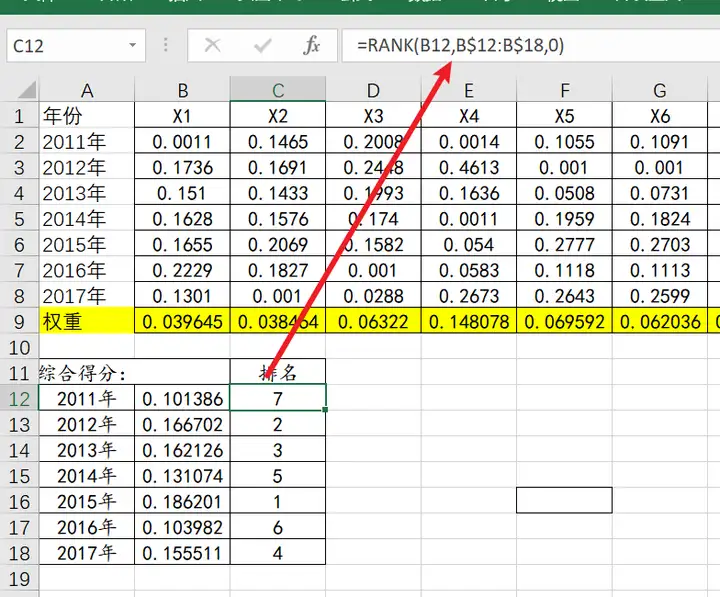
综合得分计算：
熵值法得到权重值后，此时数据与对应的权重相乘，并且进行累加，最终得到一列数据即为‘综合得分’。这里的数据指的是非负处理后的矩阵，如果没有进行非负处理，则为量纲化处理后的数据。
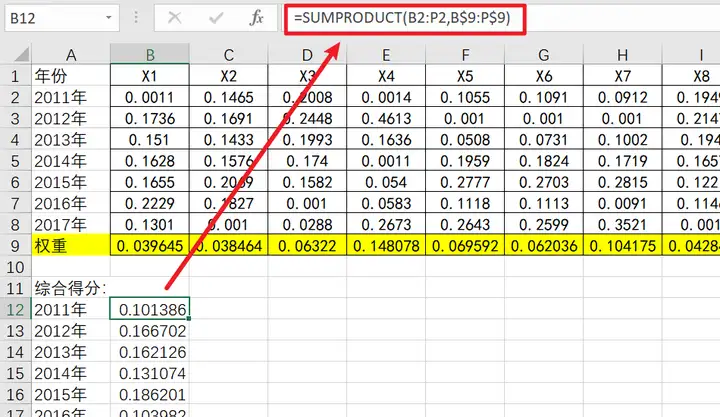
纵向对比：
