35+回归模型汇总整理,总有你想要的模型
研究自变量X与因变量Y的影响关系研究时,我们都知道最常用的就是构建回归模型,但是回归模型的种类很多,SPSSAU提供的回归模型就有20多种,应该如何确定自己需要做什么模型呢?回归模型结果又该如何分析呢?下面将相关知识进行汇总整理。
一、回归模型汇总
回归模型是研究分析自变量X与因变量Y之间的影响关系,通过构造回归模型,可以基于自变量X的值预测因变量Y的值,理解自变量如何影响因变量,以及各个自变量对因变量的影响程度。目前在SPSSAU系统中,回归模型包含以下三十多种,一句话概括说明如下:
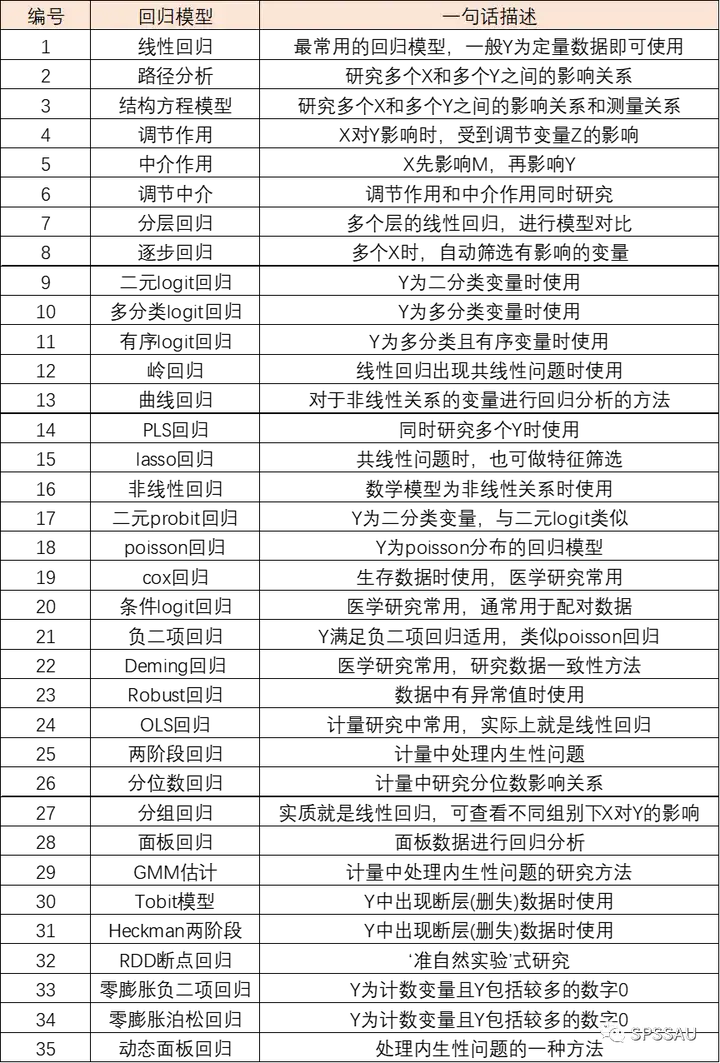
同学们可能会感到疑惑,就研究X与Y之间的影响关系,为什么会出现如此多的回归模型?这在因为研究X对于Y的影响时,会区分出很多种情况:比如因变量Y的数据类型,可能是定类数据也可能是定量数据;Y的个数可能有1个或多个;同时每种回归分析还有很多前提条件,如果不满足则有对应的其它回归方法进行解决。这也就解释了为什么会有如此多的回归分析方法。
那么面对如此多的回归模型,第一次写论文的同学们应该如何选择呢?
二、回归模型选择
论文写作用中回归模型的选择,通常需要结合X和Y的数据类型和个数进行确定。
1、数据类型
通常在SPSSAU中,为了通俗易懂我们将数据分为两大类:定类数据和定量数据
- 定量数据:数字大小具有比较意义
例如:GDP、身高、体重、工资、量表题选项(1,2,3,4,5)等等
- 定类数据:数字大小仅代表分类,不具有比较意义
例如:性别(如1和0分别代表男和女,不具有比较意义)、学历、职位等
2、回归模型初步判断
回归分析方法初步判断方法如下:
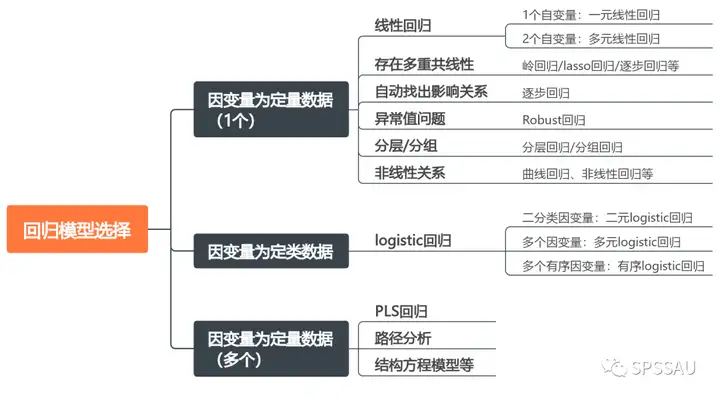
(1)因变量为定量数据(仅1个)
当因变量为定量数据且只有1个时,一般线性回归模型比较常用。线性回归模型是当前使用最为成熟,研究最多的回归分析方法之一。
线性回归模型有很多需要满足的前提条件(如线性、独立性、正态性、方差齐等),如果不满足这些假定或者条件可能会导致模型使用出错,那么此时就有对应的其它回归模型出来解决这些问题,因而跟着线性回归后面又出来很多其他回归分析方法。
比如:如果自变量间出现多重共线性问题(VIF值大于10),那么可以使用岭回归、lasso回归、逐步回归等回归模型;如果X个数非常多,想要模型自动找出对Y有影响的X,可以使用逐步回归模型;若数据中有异常值,可以使用Robust回归模型;如果要对X进行分层或者分组,则使用对应的分层回归或者分组回归;若研究的数据不满足线性关系,则选择对应的非线性回归模型,如SPSSAU中提供的曲线回归和非线性回归方法中提供60多种非线性关系模型。
(2)因变量为定类数据
当因变量为定类数据时,一般logistic回归模型比较常用。
- 因变量为二分类变量时,比如“买&不买”、“阳性&阴性”,选择二元logistic回归分析;
- 因变量为多分类变量时,比如村长候选人“甲、乙、丙”,选择多分类logistic回归分析;
- 因变量为多分类变量且有序时,比如“不满意、一般、满意”,选择有序logistic回归分析。
(3)因变量为定量数据(多个)
在进行X对于Y的影响关系研究时,如果研究人员希望将多个Y同时放一起分析时,可以使用PLS回归模型。除此之外,若要研究多个X与多个Y之间的影响关系还可以使用路径分析或者结构方程模型。路径分析只研究变量间的影响关系,而结构方程模型同时研究变量间的影响关系和测量关系。
以上为比较常见的回归模型初步选择的说明,其中提到的回归方法都是在实际研究中使用频率较高的。
三、回归模型分类
下面对一些常用的回归模型按应用领域进行分类,大家可以结合自己的研究方向选择对应的回归模型,分类说明如下:

1、通用型
通用型回归模型几乎在所有领域都适用,包括线性回归、逐步回归、logistic回归等(点击方法名称一键直达帮助手册)。
线性回归是最基本的回归模型,Y为1个定量数据,如果回归模型中X仅为1个,此时就称为简单线性回归或者一元线性回归;如果X有多个,此时称为多元线性回归。
逐步回归是一种选择最佳回归模型的方法,它通过逐步引入变量来筛选出对因变量有显著影响的自变量,从而构建最优的回归模型。当X个数很多时,可以让系统自动识别出有影响的X,这一自动识别分析方法则称为逐步回归分析。
逻辑回归则是一种用于解决分类问题的回归模型,如果Y为二分类变量比如0和1(比如1为愿意和0为不愿意,1为购买和0为不购买),此时使用二元logistic回归;如果Y为多分类,此时使用多分类logistic回归;如果Y为多类且有序(比如不喜欢,一般,喜欢),此时可以使用有序logistic回归。
2、计量角度
在计量经济学研究中,比较常用的回归模型有Robust回归、OLS回归、两阶段回归、分位数回归、Possion回归、负二项回归等(点击方法名称一键直达帮助手册)。
Robust回归法其适用于解决异常数据(或极端数据)时的回归估计。
OLS回归研究X对于Y的影响,在计量研究中,异方差问题非常重要,严重的异方差问题会影响模型估计和模型检验等,因而在OLS回归时需要对其进行检验,如果出现异方差问题则需要进行处理等。实际上也是线性回归,在计量经济学中比较常用。
计量经济学中,解决内生性的一种方法。
如果想看出X对于Y的影响关系及影响趋势情况,则可以使用分位数回归;其原理是将数据按因变量进行拆分成多个分位数点,研究不同分位点情况下时的回归影响关系情况。
如果数据符合Poisson分布时(数据满足平稳性、独立性、普通性),而又想研究X对于Y的影响(Y呈现出Poisson分布);此时则需要使用Poisson回归,而不是使用常规的线性回归等。
针对Possion回归来讲,如果计数资料不适合Poisson分布时,尤其是数据过离散时,此时使用负二项回归分析更合适。
面板数据是指不同对象在不同时间上的指标数据。面板数据进行回归影响关系研究时,即称为面板模型(面板回归)。
如果在面板模型中,解释变量包括被解释变量的滞后值,此时则称之为“动态面板模型”,其目的是处理内生性问题。
实质是线性回归,比如将性别分为男和女,分别做线性回归并且对比参数值。
比如第一次放入4个X、第二层放入3个X、第3层放入2个X,每一层均在上一层基础上放入更多项;那放入的更多项是否对模型有解释力度,此则为分层回归关心的问题。
在计量经济学中,处理内生性问题的一种方法。
用于解决‘删失/受限被解释变量’这种问题,如果被解释变量中的数据有出现‘删失/受限’,此时进行ols回归并不科学。
被解释变量出现‘断层’(删失),可使用Heckman两阶段模型进行研究(而不是常用的ols线性回归)。
3、社科学角度
在社会科学研究领域,常用的回归模型有路径分析、结构方程模型、调节作用、中介作用等,它们不是严格意义上的回归模型,但是本质也是研究影响关系的模型(与上面重复的回归模型不再赘述)。
研究模型影响关系,用于对模型假设进行验证。比如下图的模型框架:希望研究工作条件,人际关系对于公司满意度的影响;同时还希望研究公司满意度和机会感知对于离职倾向的影响,路径有一共有4条(即4对影响关系)。
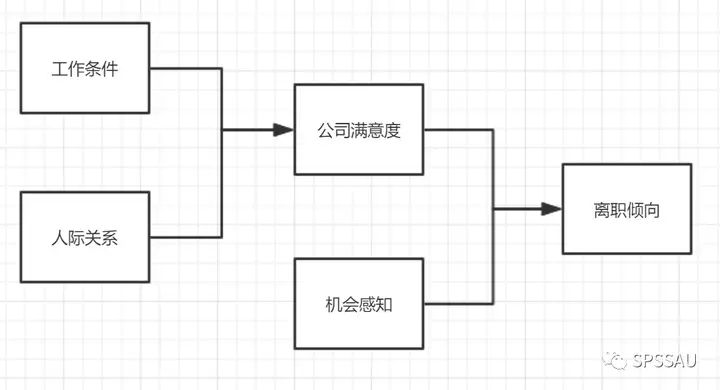
结构方程模型SEM是一种多元数据分析方法,其可用于研究多个潜变量之间的影响关系情况。结构方程模型共包括两部分结构,分别是测量关系和影响关系(路径分析只有影响关系)。
调节作用是研究X对Y的影响时,是否会受到调节变量Z的干扰;比如开车速度(X)会对车祸可能性(Y)产生影响,这种影响关系受到是否喝酒(Z)的干扰,即喝酒时的影响幅度,与不喝酒时的影响幅度 是否有着明显的不一样。
中介作用是研究X对Y的影响时,是否会先通过中介变量M,再去影响Y;即是否有X->M->Y这样的关系;比如工作满意度(X)会影响到创新氛围(M),再影响最终工作绩效(Y)。
同时研究调节作用和中介作用。
4、医学角度
医学领域常用的回归模型有二元probit回归、条件logit回归、Cox回归、Deming回归、Possion回归、负二项回归等。
二元probit回归模型的使用场景与二元logit回归保持一致。二者的区别在于连接函数的不同。在实际应用中,二元logit回归的使用更为广泛,通常情况下无法严格的进行区分,建议医学、经济金融类相关学科可以使用二元probit模型;其它学科使用二元logit回归模型。
医学研究的病例-对照研究中,为了控制一些重要的混杂因素,经常会把病例和对照按年龄,性别等条件进行配对,形成多个匹配组。各匹配组的病例数和对照人数是任意的,比如一个病例和若干个对照匹配即1:1,常见是1:M(M <=3),即1个病例和1或2或3个对照匹配。也或者在使用过计量研究里面的PSM倾向得分匹配,也有可能使用到条件logit回归。
是一种研究影响生存时间的方法,由于生存时间数据的特殊性,因而此模型的因变量会涉及两项,分别是生存时间和生存状态。
可用于研究两种仪器(或者两种测量方法等)是否有着一致性(相似的测量值)。Deming回归与普通线性回归(OLS回归)的原理上有所不同,普通线性回归时,只有Y会包含测量误差,但是Deming回归时X和Y均会包含测量误差。
四、软件操作与结果解读
以最常用的多元线性回归模型为例,介绍如何使用SPSSAU软件快速完成模型构建与分析。
(1)SPSSAU操作
分析页面左侧选择分析方法->拖拽数据至右侧对应分析框->点击开始分析
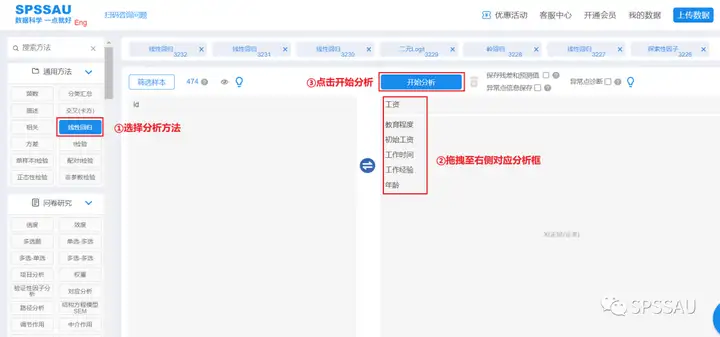
(2)结果解读
SPSSAU输出多元线性回归分析结果如下:
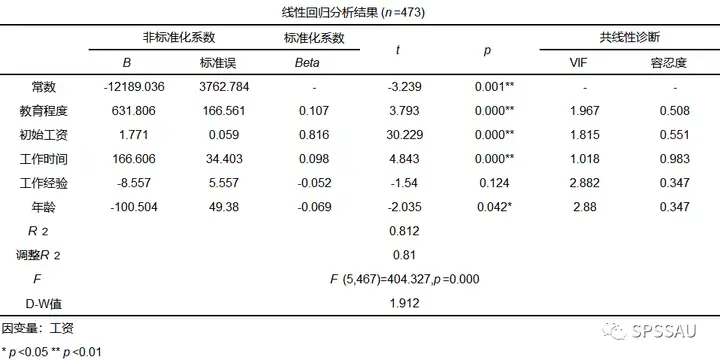
回归分析结果解读可以参考SPSSAU表格下方的分析建议与智能分析:
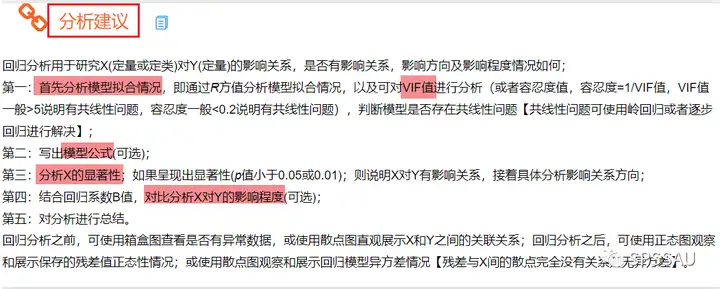

今天有关回归模型的内容就分享到这里。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号