回归模型和分类模型
在进行模型构建与分析时,模型评价是非常关键的一步。合适的评价指标可以帮助我们准确地衡量模型的性能,从而进行优化和改进。然而,不同的模型和应用场景需要使用不同的评价指标。下面将分别介绍回归模型与分类模型常用的一些评价指标。
一、回归模型评价指标
回归模型常用的评价指标可分为以下三大类:
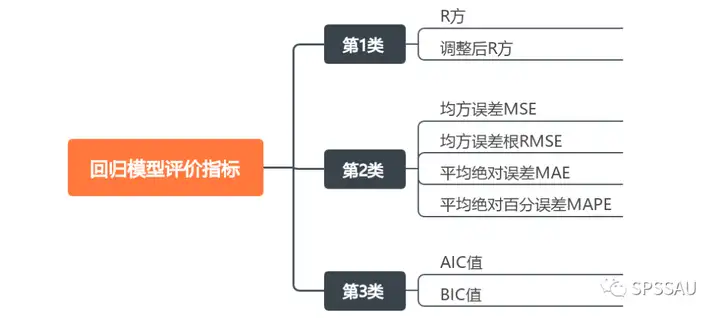
- 第1类:回归模型拟合优度的评价指标,包括R方与调整后R方值;
- 第2类:回归模型拟合值与真实值的差异程度的评价指标,常用的包括MSE、RMSE、MAE、MAPE;
- 第3类:极大似然法的估计准则,包括AIC值和BIC值。
接下来,分别进行介绍说明。
1、拟合优度R方
R方值是衡量回归模型拟合优度的统计量,它表示回归模型对观测值的拟合程度,代表了模型中因变量可由自变量解释的百分比。R方值的取值范围在0到1之间,R方值越大,说明回归模型对观测值的拟合程度越好。比如R方为0.5,说明所有自变量可以解释因变量50%的变化原因。
R方计算公式如下
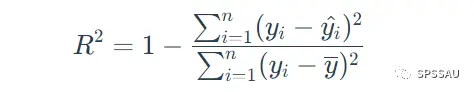

2、调整后R方
调整后R方是修正自由度的决定系数,在多元线性回归中,R方有个致命的问题,那就是随着自变量X的个数增加,R方会越来越大,R方越来越大就会认为模型拟合越来越好,但是实际上可能是由于自变量个数的增加导致的R方增大。这样看来,R方就不是一个比较客观的指标,此时将自变量个数考虑进公式中,就得到了调整后R方。
调整后R方计算公式:
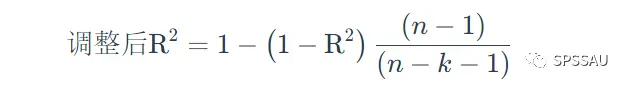
从公式可以看出,调整后的R方同时考虑了样本量n和自变量个数k,且调整后R方不会随自变量个数的增大而增大。
- SPSSAU结果展示:
SPSSAU进行回归模型分析时,输出R方与调整后R方展示如下(以多元线性回归为例):
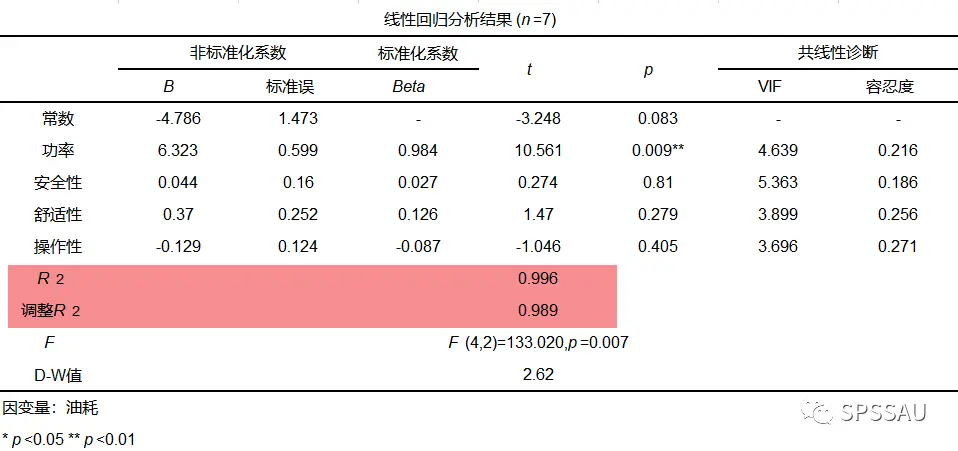
3、均方误差MSE
上述R方指标用于衡量模型可解释的因变量的百分比,但在一些情况下,我们可能更关注模型的拟合值与真实值的差异程度,需要计算模型平均残差的指标。因为假设残差服从正态分布,意味着残差的均值将始终为0,所以可计算均方误差MSE、均方误差根RMSE、平均绝对误差MAE。
均方误差MSE(又称L2范数损失),即误差平方和的平均值,MSE是衡量模型预测误差的一种常用指标。MSE值越接近于0,说明模型拟合越好。
MSE计算公式:
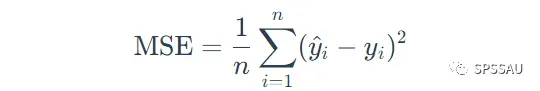
4、均方误差根RMSE
均方误差根RMSE,是均方误差MSE的算术平方根,回归模型中最常用的评价模型指标。相比于均方误差MSE,均方误差根RMSE更常用。RMSE值越接近0,说明模型拟合越好。
RMSE值计算公式:
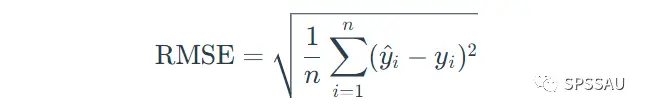
5、平均绝对误差MAE
MSE值和RMSE值受异常值残差影响较大,因此可使用平均绝对误差MAE(又称L1范数损失),即误差绝对值的平均值。MAE可以准确反映实际预测误差的大小。MAE用于评价真实值与拟合值的偏离程度,MAE值越接近于0,说明模型拟合越好,模型预测准确率越高(但是RMSE值还是使用最多的)。
MAE计算公式:
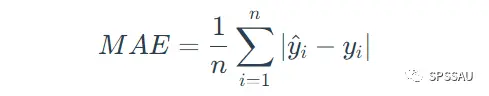
6、平均绝对百分误差MAPE
平均绝对百分比误差MAPE是平均绝对误差MAE的变形,该值采用百分比的形式,不受异常值的影响。MAPE不仅考虑了拟合值与真实值之间的误差,还考虑了误差与真实值之间的比例,MAPE的值越小,说明模型越好。
MAPE计算公式:
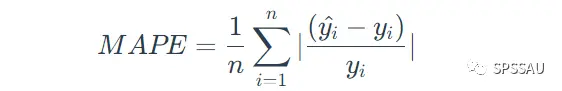
除以上指标外,还有很多其他的模型评价指标,如中位数绝对误差MAD、可解释方差分EVS,均方根对数误差MSLE等,只是这些指标相对于以上4种使用少很多。
- SPSSAU结果展示:
SPSSAU进行相应的回归模型分析时,也会自动输出上面提到的评价指标,如机器学习模块进行回归模型分析时输出模型评估结果展示如下:

7、AIC准则和BIC准则
线性回归、逻辑回归、泊松回归、负二项回归等很多类型的回归模型,都是使用极大似然法对参数进行估计。极大似然法的估计准则包括赤池信息准则(AIC)、贝叶斯信息量准则(BIC)。
AIC准则的表达式如下:
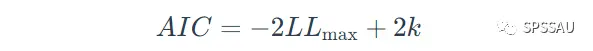
上式中,LLmax是对数似然估计值,k是参数数量。BIC准则的表达式如下:
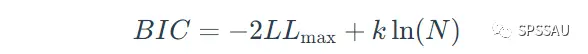
N是样本大小。
可通过比较AIC、BIC值的大小来比较模型的拟合效果,如果模型的AIC值和BIC值越小,说明模型估计越准确。
- SPSSAU结果展示:
在进行相应回归模型分析时(如线性回归、logistic回归、负二项回归、Poisson回归等),SPSSAU均会自动输出AIC值、BIC值供用户对比使用。如下表为二元logistic回归分析输出的AIC与BIC值:

二、分类模型评价指标
分类模型常用的评价指标可分为以下两大类:
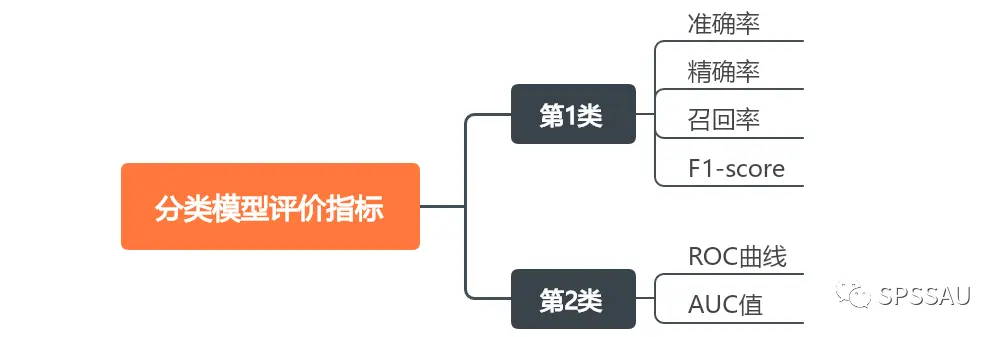
接下来分别进行介绍。
1、准确率、精确率、召回率、F1-score
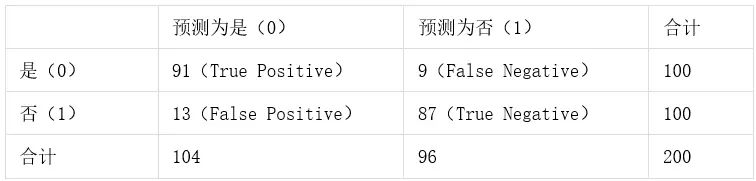
准确率、精确率、召回率、F1-score是模型评价中常见的指标,以下表为例,进行介绍说明:
(1)准确率
准确率是指分类正确的样本占总样本个数的比例。即Accuracy=(TP+PN)/(TP+FP+FN+TN)
以上表为例,该模型的准确率为Accuracy=(91+87)/200=0.89
准确率是分类模型中最简单也是最直观的评价指标,但同时存在明显的缺陷,这个评价指标很容易受到样本数量以及样本是否均衡带来的影响。
(2)精确率
精确率是指分类模型中正确的正样本个数占分类器判定为正样本的样本个数的比例。精确率容易与准确率混淆,精确率只针对预测正确的正样本而不是所有预测正确的样本。即Precision=TP/(TP+FP)上表中,该模型的精确率Precision=91/(91+13)=0.875
(3)召回率
召回率是指分类正确的正样本个数占真正的正样本个数的比例。即Recall=TP/(TP+FN)
上表中,该模型的召回率Recall=91/(91+9)=0.91
(4)F1-score
F1值是精确率和召回率的加权调和平均数,精确率和召回率都是越高越好,但两者往往是矛盾的。因此常用F1-score来综合评价分类器的效果,它的取值范围为0到1,越接近1效果越好。
F1=2*Precision*Recall/(Precision+Recall)那么,上表该模型的F1-score=2*0.875*0.91/(0.875+0.91)=0.892
- SPSSAU结果展示
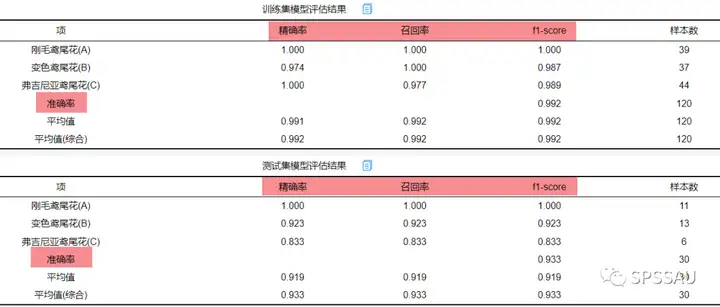
SPSSAU机器学习模块进行分类模型分析时,输出评价指标展示如下:
2、ROC曲线和AUC值
ROC(Receiver Operating Characteristic,受试者工作特征)曲线和AUC值常用来评价二分类器的优劣。ROC曲线如下图所示:
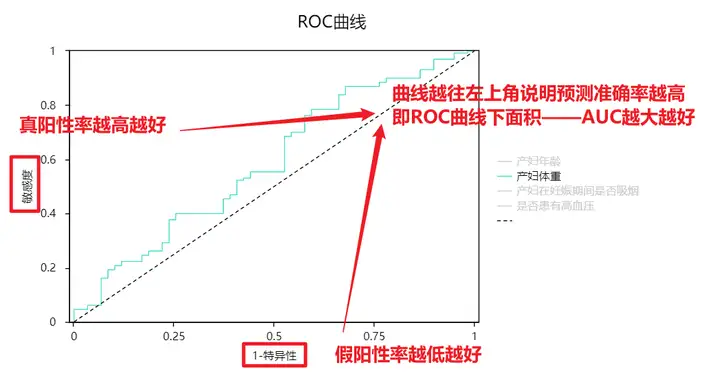
ROC曲线纵坐标为敏感度——阳性人群中,检测出阳性的概率,希望该值越高越好;横坐标为1-特异性——阴性人群中,检测为阳性的概率,希望该值越低越好。结合横纵坐标的概念,可以得到结论:曲线越往左上角说明预测准确率越高。
当使用ROC曲线对多个分类器进行评级时,直接使用ROC曲线进行肉眼比较是非常不方便的,此时就需要一种定量指标进行对比,那么这个指标就是AUC值——ROC曲线下面积,AUC值越大,分类器效果越好。
AUC取值范围通常在0.5~1之间:AUC<0.5,说明模型比随机猜测还差,因此不存在该情况;
AUC=0.5,与随机猜测一样(比如扔硬币),模型没有预测价值;0.5<AUC<1,优于随机猜测,有预测价值;
AUC=1,完美分类器,理论上存在,但绝大多数场景下,不存在完美分类器。
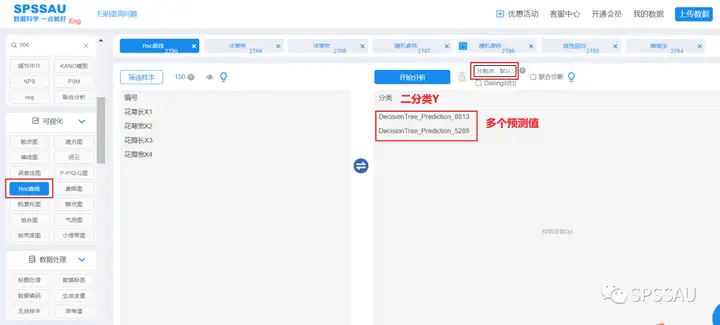
- SPSSAU软件如何将多个模型绘制ROC曲线对比优劣?
- 如果涉及多个模型预测能力绘制ROC曲线,用于多个模型预测能力对比。建议按以下步骤进行:
- 第1步:得到各个模型(比如神经网络模型、随机森林模型、二元logistic回归模型等)的预测值标题,该预测值可通过SPSSAU中‘保存预测值’参数选中后得到;
- 第2步:将得到的预测值作为ROC曲线时的‘检验变量X’。此时绘制出来的ROC曲线则会有多条,分别表示各模型的预测值。与此同时,ROC曲线时的‘状态变量Y’为实际真实情况上的Y数据,并且该数据正常情况下为二分类(即仅包括2个数字即两个类别)。
ROC曲线操作如下图: