医学案例|概要t检验

一、案例介绍

通过以往大量资料得知某地20岁男子平均身高为168cm，今随机测量当地16名20岁男子，得到其身高均数为172cm，标准差为14，问当地现在20岁男子的平均身高是否比以往高？

二、问题分析

从案例来看，要分析16名男性平均身高是否高于以往平均身高168cm，即比较样本均数所来自的总体均数是否高于已知的总体均数，可以使用单样本t检验进行分析。根据经验，身高服从正态分布，所以满足使用单样本t检验的前提条件。但是当前只有汇总数据（平均值、标准差、样本量），并没有原始数据，所以可以通过SPSSAU概要t检验使用汇总数据进行分析。

三、软件操作及结果解读

（1）单样本t检验

先手算介绍一下单样本t检验的分析过程。

①建立假设检验，确定检验水准：

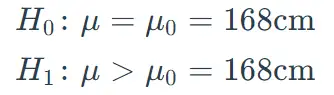
\begin{aligned}H_0\colon\mu&=\mu_0=168\mathrm{cm}\\H_1\colon\mu&>\mu_0=168\mathrm{cm}\end{aligned}

原假设为现在该地20岁男子的平均身高与以往20岁男子的平均身高相等；

备择假设为现在该地20岁男子的平均身高高于以往20岁男子的平均身高。

②计算检验统计量：

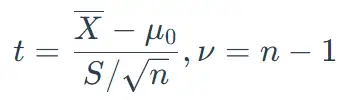
t=\frac{\overline{X}-\mu_{0}}{S/\sqrt{n}},\nu=n-1

本案例n=16，\overline{X}=172cm，S=14cm，\mu_0=168cm

代入计算得

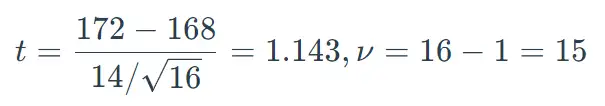
t=\frac{172-168}{14/\sqrt{16}}=1.143,\nu=16-1=15

③确定p值，做出推断结论：

查t界值表，得单侧概率0.10<p<0.20，按α=0.05水准，不拒绝原假设，差异无统计学意义，即不能认为该地20岁男子平均身高比以往更高。

手算比较麻烦，接下来介绍使用SPSSAU快速完成分析。

（2）软件操作

在SPSSAU【实验/医学研究】模块，选择【概要t检验】，具体选择“单样本t检验”，分别填写汇总数据，操作如下图：

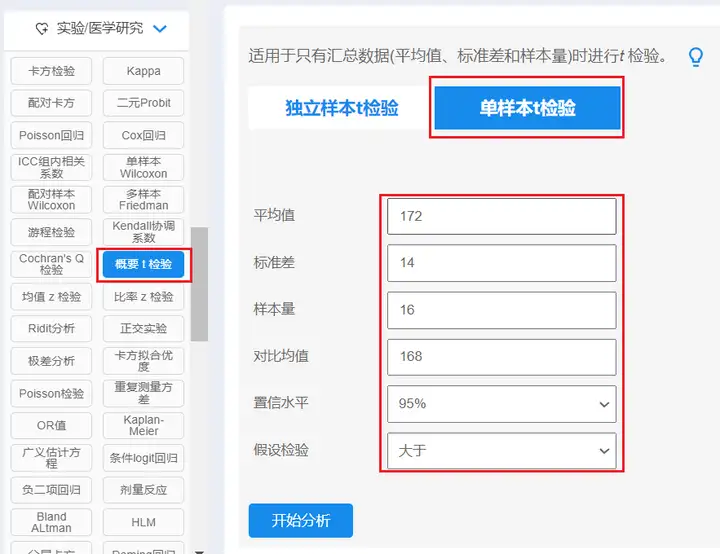
分析中设计两个统计学名词，置信水平和假设检验，说明如下：

①置信水平：置信水平是指总体参数值落在样本统计值某一区内的概率；指在多大程度上对假设有把握，通常为95%，可选为99%和90%。

②假设检验：原假设是等于，小于，还是大于。

本案例中，设置置信水平为95%，因为要研究均值172cm是否明显大于168cm，所以假设检验选择“大于”。如果研究是否等于或小于168cm则对应选择假设检验为“等于”或“小于”。

（3）结果解读

SPSSAU输出分析结果如下：

①单样本t检验置信区间

本次收集样本为16个20岁男子身高，平均值为172cm，标准差为14cm，分析显示身高的95% CI为：164.5399cm~179.4601cm。即有95%的把握身高应该介于164.5399cm到179.4601cm之间。

②单样本t检验假设检验

分析上表可知：本案例预判断16名20岁男子身高172cm，是否明显高于168cm，检验显示t=1.1429，p=00.8645>0.05不拒绝原假设，差异无统计学意义，即不能认为该地20岁男子平均身高比以往更高，该结论与手算结论一致。

四、结论

通过使用SPSSAU概要t检验中的单样本t检验分析得知，现在该地20岁男子的平均身高172cm与以往20岁男子的平均身高168cm的差异无统计学意义（t=1.1429，p=00.8645>0.05），所以不能认为该地20岁男子平均身高比以往更高。

五、知识小贴士

（1）独立样本t检验的3个名词术语什么意思？

①对比均值(差值对比)：独立t 检验时，对比数字是指两组数据均值差，与某个数字进行对比，通常情况下是0（即两组数据平均值差值，与数字0进行对比PK）。

②置信水平：指在多大程度上对假设有把握，通常为95%，可选为99%和90%。

③假设检验：原假设是等于，小于，还是大于，通常情况下等于（即直接对比是否相等，即是否有差异）。

（2）独立样本t检验分析前提条件？

针对独立样本t 检验，从原理上，其需要先判断方差齐，方差齐和不齐时计算标准误的公式并不一样。此检验过程已经被SPSSAU进行自动判断，并且自动给出对应的计算结果。