箱线图如何绘制？

一、案例介绍

某研究者在一项回顾性调查中搜集了部分资料，其目的是研究抗生素的使用效果，数据为某医院内、外科25例住院患者使用抗生素的情况，想要使用可视化图形进行比较用与不用抗生素的住院患者住院天数的差异以及数据是否存在异常值。

二、问题分析

本案例的分析目的是想要使用可视化图形进行比较用与不用抗生素的住院患者住院天数的差异以及数据是否存在异常值。对此，为了解决该问题，可以使用箱线图进行查看与比较，箱线图一般用于多组计量资料的分布比较，一般会提供5个基本统计量，其中包括最小值、第一四分位数、第二四分位数、第三四分位数以及最大值。并且箱线图还可以直观查看到数据中是否含有异常值。所以使用箱线图进行分析比较合适。

三、软件操作及结果解读

(一) 数据导入

1.数据格式

首先将数据整理成正确的格式然后进行上传，一般一列为一个指标，由于指标涉及“用与不用抗生素”所以需要上传带有标签的数据，比如1代表是，2代表否，整理如下：

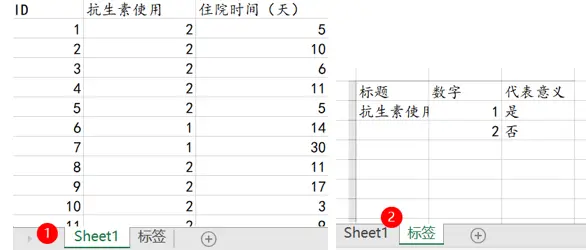
2.导入数据

将整理好的数据导入到SPSSAU系统内，点击页面右上角“上传数据”按钮，点击上传文件，将数据进行上传即可，如下：

将数据上传到系统内。上传结果如下：

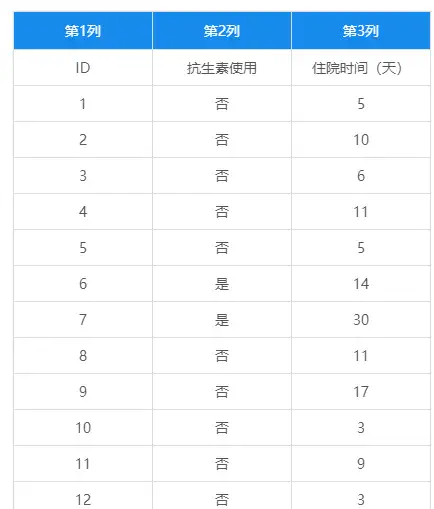
(二) 绘制箱线图

1.软件操作

箱线图可以反映原始数据分布的特征，还可以进行多组数据分布特征的比较，其绘制方法一般是先找出一组数据的上限、下限、中位数和两个四分位数，然后，连接两个四分位数画箱子，再将上限和下限与箱子连接，中位数在箱子中间。箱线图如何操作以SPSSAU为例，点击【可视化】→【箱线图】进行分析。操作如下：

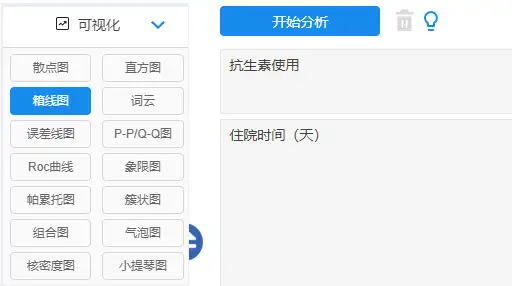
2. 结果解读

结果如下：

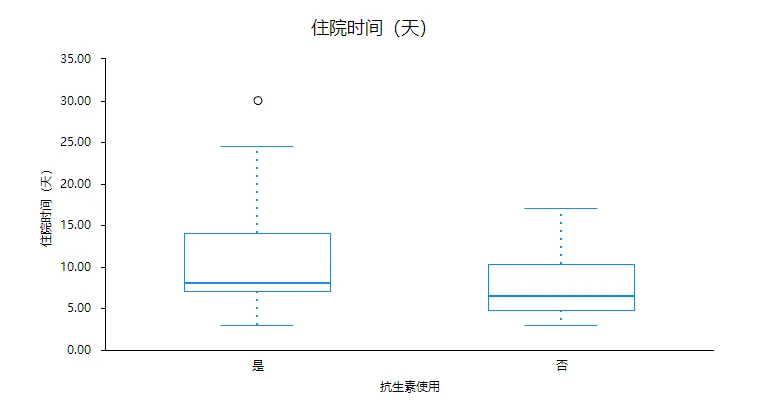
从分析结果可以看出，使用抗生素的患者住院天数整体上要高于没有使用抗生素的患者住院天数。具体数值如下：

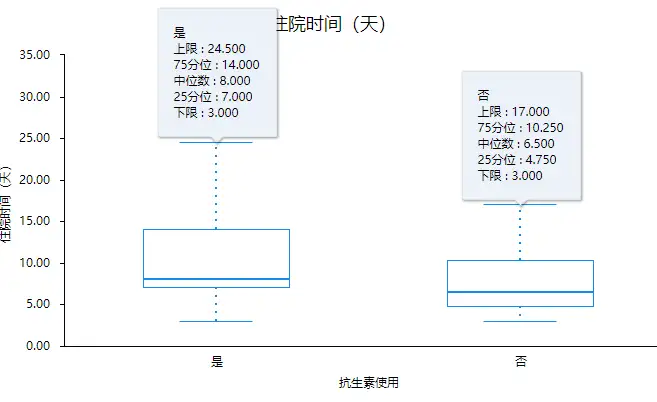
SPSSAU箱线图共由五个数值点构成，分别是最小观察值（下限），25%分位数（Q1），中位数，75%分位数（Q3），最大观察值（上限）。最小观察值和最大观察值定义如下：

最小观察值 = Q1 – 1.5（IQR四分位差）, IQR = Q3 –Q1

最大观察值 = Q3 + 1.5（IQR四分位差）, IQR = Q3 –Q1

箱线图中，‘下限’为最小观察值与真实最小值之间的较大值；‘上限’为最大观察值与最大值之间的较小值。

并且从图中发现使用抗生素的住院天数有一个异常值，具体异常值如下：

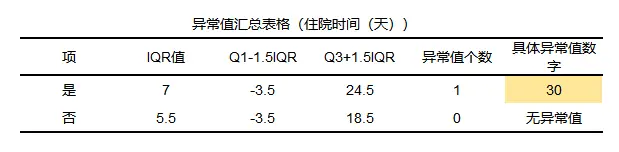
可以看到数据有一个异常值，异常值为“使用抗生素的住院天数”数据组中的30，“未使用抗生素的住院天数”中没有异常值。异常值的判断标准如下：如果数据出现大于 Q3+1.5IQR（极大值），则为异常值，也或者数据小于 Q1-1.5IQR（极小值），则为异常值。

四、结论

所以通过箱线图的查看，我们发现使用抗生素的患者住院天数整体上要高于没有使用抗生素的患者住院天数。，并且“使用抗生素的住院天数”数据组中有一个异常值30，如果后续进行其它分析需要将异常值筛选后分析，以免因为异常值导致分析结果不准确或者出现其它情况。

五、知识小贴士

1、极大值和极小值，最大值和最小值问题？

箱线图里面的极大值并非最大值，极小值也不是最小值。其计算公式为：最小观察值 =Q1 - 1.5（IQR）, IQR = Q3 –Q1；最大观察值 =Q3 + 1.5（IQR）, IQR = Q3 –Q1

2、箱线图共有两个用途。

分别如下：

直观地识别数据中异常值（离群点）；

直观地判断数据离散分布情况，了解数据分布状态。