三因素方差分析
一、案例介绍
在治疗肝癌的药物研究中，为了提高治疗药物在靶器官——肝脏的浓度，降低在非靶器官如心脏的浓度，设置了3个因素，第一个因素是药物（A），有2个水平，分别为“丝裂霉素+高分子物质+磁性物质”（实验组）和“丝裂霉素”（对照组）；第二个因素是时间（B），有3个水平，分别为给药后15分钟、30分钟和60分钟；第三个因素是器官（C），有两个水平，分别为肝脏和心脏，将60只小鼠随机分为12组（即2*3*3种组合），每组5只，即重复例数为5.观察指标（反应变量）为组织中丝裂霉素的浓度（ug/g）。想要研究不同条件的因素A、B、C对丝裂霉素的浓度是否有差异，以及交互项等是否存在显著差异。
二、问题分析
例子中涉及四个变量，一个是“药物”一个是“时间”一个是“器官”还有一个是“丝裂霉素浓度”。其中“药物”、“时间”和“器官”是定类变量，“丝裂霉素的浓度”是定量变量，研究不同条件的因素A、B、C对丝裂霉素的浓度是否有差异，以及交互项等是否存在显著差异。这就是一个三因素方差分析问题。
三、软件操作及结果解读
(一) 数据导入
1.数据格式
首先将数据整理成正确的格式，有三个X，一般一个X为一列，Y为一列，并且分析的数据带有数据标签的，需要另添加一个表格进行说明，数据格式如下：
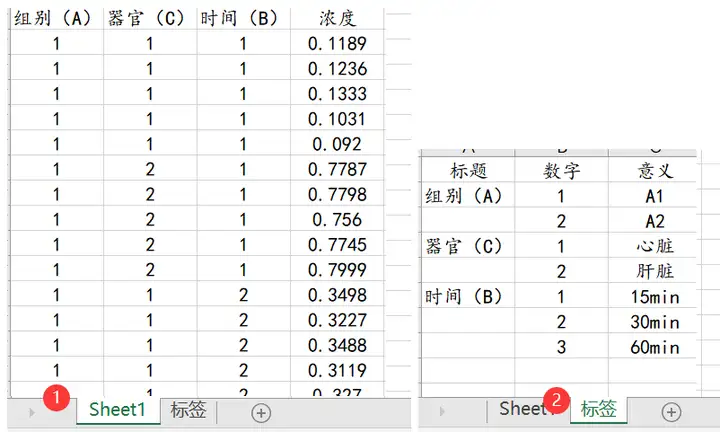
2.导入数据
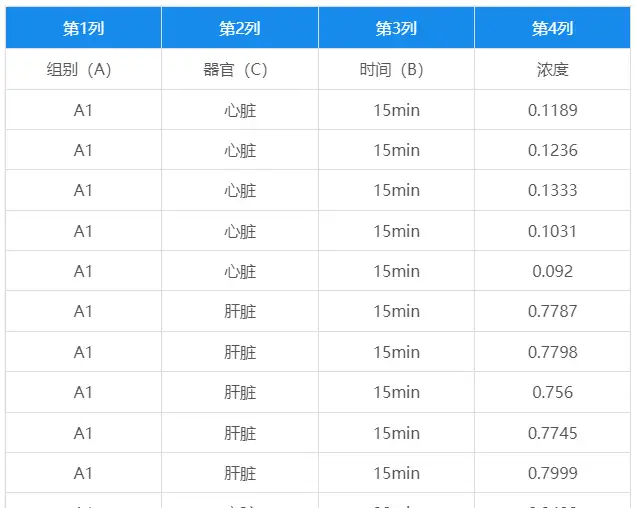
将整理好的数据上传至SPSSAU系统内，如下：
上传结果部分如下：
(二)三因素方差分析
为了研究不同“药物”、“时间”和“器官”对小鼠体内丝裂霉素是否有显著差异以及两个或三个因素搭配是否对丝裂霉素浓度产生新的影响，以不同药物、不同时间和不同器官为自变量，以小鼠体内丝裂霉素浓度作为因变量进行三因素方差分析。
- 软件操作
上传数据后点击【进阶方法】→【三因素方差分析】然后进行分析：
- 主效应
主效应简单来说就是X对Y的影响。比如：三因素方差分析中，分别去判断“组别”、“时间”和“器官”对丝裂霉素的浓度的影响。
结果如下：
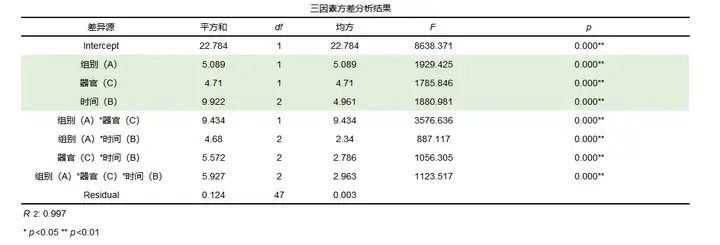
首先进行查看变量“组别”，发现自变量组别的F值为1929.425，并且p值小于0.05所以说明主效应存在，然后对“器官”进行分析，发现时间的F值为1785.846并且p值小于0.05所以说明主效应存在，最后对“时间”进行分析，发现时间的F值为1880.961并且p值小于0.05，说明主效应存在，说明不同组别、不同器官的处理以及不同时间的处理对小鼠体内的丝裂霉素浓度均具有显著性差异。接下来研究“组别”、“时间”和“器官”搭配是否对丝裂霉素浓度产生新的影响，进行查看二阶效应。
3.二阶效应
三因素方差分析中，如果除了研究单个X对Y的影响，还想研究三个X中两两组合对Y的影响，例如例子中的某个组别的不同处理时间对小鼠体内丝裂霉素浓度是否有影响，则为交互作用分析，即二阶效应。
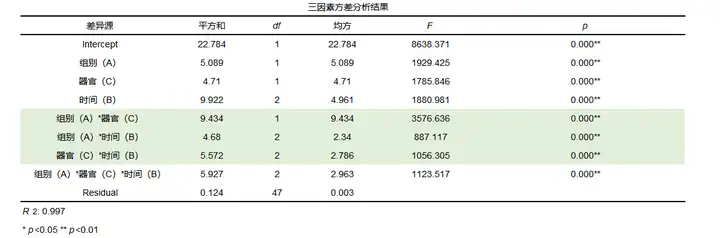
三个自变量两两进行组合一共有三个分析项，组别*器官、组别*时间、器官*时间三个分析项对丝裂霉素是否有影响。可以发现组别*器官、组别*时间、器官*时间三个分析项的p值均小于0.05，说明模型均具有显著性。三因素方差分析处了分析主效应，交互效应外，还可以进行分析三个因素一起组合对丝裂霉素浓度是否有影响即三阶效应。
4.三阶效应
结果如下：
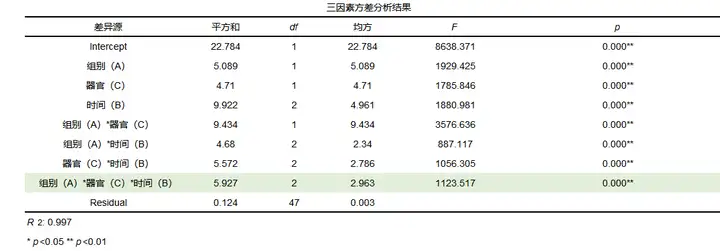
三个变量进行组合形成变量“组别*器官*时间”，发现该分析项的F值为1123.517并且p值小于0.05，所以说明组别*器官*时间对小鼠丝裂霉素浓度具有显著性差异，所以说明该模型的三阶效应存在。
由上述分析结果发现所有主效应之间存在统计学差异，并且各个交互效应也具有显著意义，因而可以进一步分析。
三因素均值对比：
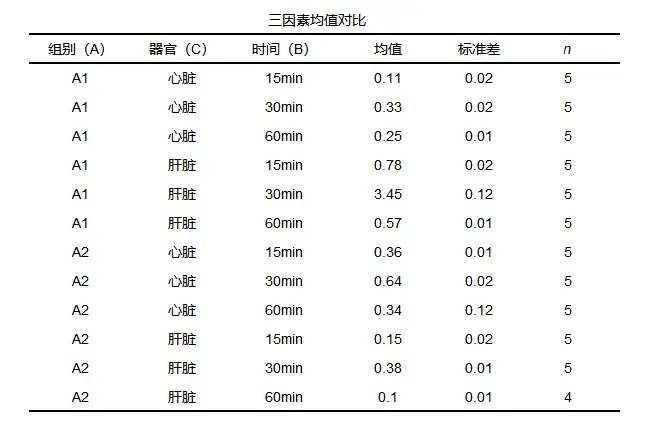
上表格可以得到基本信息，具体对比可以查看如下折线图：
（1）组别和器官的均值对比图
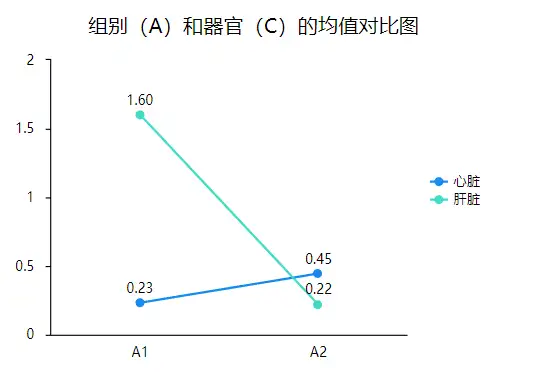
从折线图中可以发现，A1为实验组，A2为对照组，实验组肝脏的浓度显著高于心脏，而对照组肝脏的浓度却低于心脏。
（2）组别和时间的均值对比图
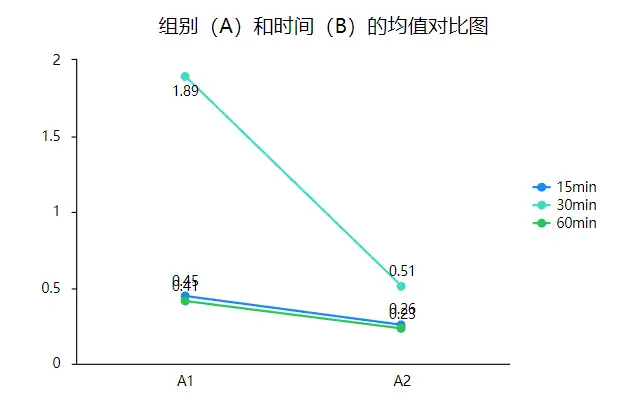
从上图可以看出药物分布在给药后的30min药物浓度达到最大，15min和60min相差不大。
（3）器官和时间的均值对比图
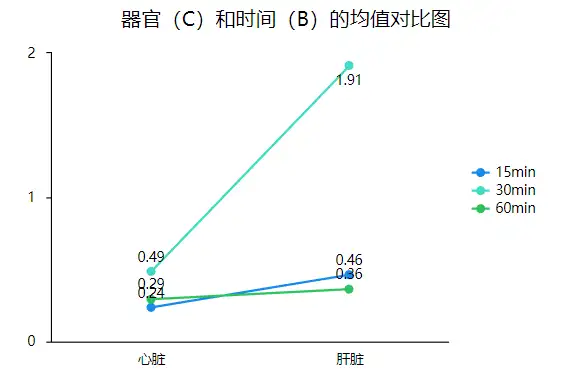
从上图可以看出心脏给药后的30min药物浓度达到最大，并且肝脏也是给药后的30min药物浓度达到最大。根据研究目的药物在靶器官的浓度要高，以提高对肿瘤喜报的杀伤力，在非靶器官要低，以减少毒副作用。分析完毕。
四、结论
通过三因素方差分析发现不同组别、不同器官的处理以及不同时间的处理对小鼠体内的丝裂霉素浓度均具有显著性差异，并且不同交互项对小鼠体内的丝裂霉素浓度也均具有显著性差异，二阶效应存在，并且三阶效应也存在，通过进一步分析，根据折线图的对比得到：研究目的药物在靶器官的浓度要高，以提高对肿瘤喜报的杀伤力，在非靶器官要低，以减少毒副作用。分析完毕。
五、知识小贴士
1、均方平方和类型？
当前计算均方平方和，算法处理上SPSSAU默认为III型平方和。
2、简单效应是指什么？
简单效应指X1在某个水平时，X2不同水平的比较；SPSSAU进行简单效应时默认使用Bonferroni法进行计算p 值。
