频数分析拟合优度卡方检验

一、案例介绍

某医学美容院对某年425位顾客抱怨原因进行了分析，结果见下表，现在想知道这四种抱怨原因的构成比是否有差异？

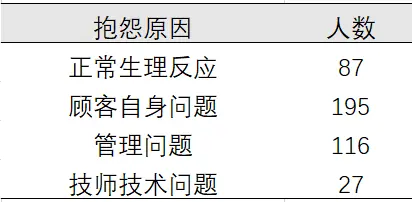
二、问题分析

本案例的分析目的是研究四种抱怨原因的构成比是否存在差异，抱怨原因为定类数据，研究定类数据的实际比例与等分比例是否存在差异可以使用频数分布拟合优度的卡方检验进行分析。

三、软件操作及结果解读

（一）理论说明

频数分布拟合优度的卡方检验，是卡方检验方法的另一种常见应用。用于判断定类数据的实际观察频数的分布是否服从某一理论期望频数分布。比如本案例为判断某一变量观察值分布是否为等比例分布。

拟合优度卡方检验建立假设检验如下：

H0：顾客抱怨原因构成比相同

H1：顾客抱怨原因构成比不同

卡方值计算公式如下：

\begin{aligned}

x^{2}& =\sum{\frac{(O-E)^{2}}{E}}={\frac{(87-106.25)^{2}}{106.25}}+{\frac{(195-106.25)^{2}}{106.25}}+{\frac{(116-106.25)^{2}}{106.25}}+{\frac{(27-106.25)^{2}}{106.25}} \\

&=137.63

\end{aligned}

其中O为实际频数，E为期望频数。得到卡方值后，查表确定p值，若p值小于0.05，则拒绝原假设，认为顾客抱怨原因构成比有差异；否则认为无差异。

（二）软件操作

在SPSSAU医学/实验研究模块，选择【卡方拟合优度】，将“抱怨原因”拖拽到右侧分析项(定类)分析框中，将“人数”拖拽到右侧“加权项”分析框中，因为本案例期望比例相同，所以不额外进行设置，SPSSAU默认期望值相等。然后点击“开始分析”，操作如下图：

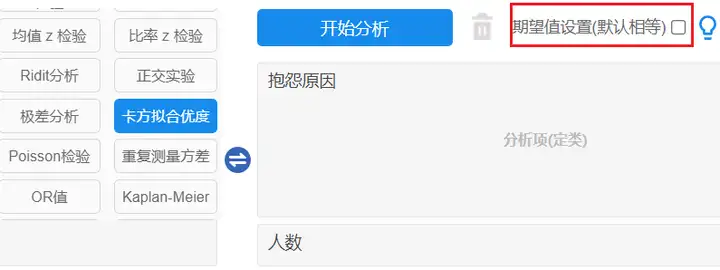
（三）结果解读

SPSSAU输出卡方拟合优度分析结果如下：

从上表可以看出，卡方值为32.7523，对应p值=0.000<0.05，按α=0.05的水平，拒绝原假设，接受备择假设，即可以认为顾客抱怨原因构成比差异有统计学意义。具体对比实际比例如下：抱怨原因中，“技师技术问题”占比最低为6.35%；其次是“正常生理反应”占比20.47%、“管理问题”占比27.29%；占比最高的为“顾客自身问题”为45.88%。可以通过SPSSAU自动输出的抱怨原因实际频数和期望频数对比图直观进行对比，如下图：

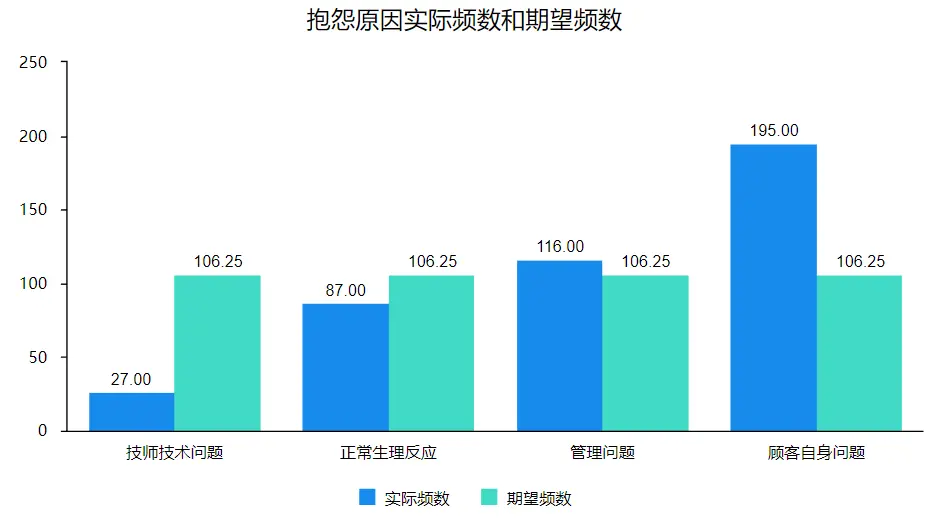
四、结论

通过频数分析拟合优度的卡方检验，研究425为顾客对医学美容院4种抱怨原因的构成比是否符合等比例分布，结果显示，卡方值为32.7523，对应p值=0.000<0.05，说明拒绝原假设，可以认为4种抱怨原因的占比差异有统计学意义，不符合等比例分布。

五、知识小贴士

• 卡方拟合优度的两种数据格式：

卡方拟合优度检验共适用两种数据格式，分别是‘加权格式’和‘不加权格式’；

1、加权格式

一列表示定类数据的类别，另一列表示各项的数量，本案例如下图：

2、不加权格式

仅用一列表示数据，100个数据即为100行，则为不加权格式，也即原始数据格式。

参考文献：

[1]颜红,徐勇勇.医学统计学.第3版[M].人民卫生出版社,2015