比率Z检验
一、案例介绍
为了解聚乙二醇400（PEG 400）对儿童功能性便秘的治疗效果，某医生将符合试验条件的216名8岁以上功能性便秘患儿随机分为试验组和对照组，实验组口服PFG400治疗，对照组口服乳果糖治疗。其中试验组105人，两周缓解76人；果乳糖组111人，两周缓解49人。试比较试验组和对照组治疗后便秘的两周缓解率有无差别。
二、问题分析
本案例研究目的是比较两组比率是否有差别，且试验组和对照组样本量较大，所以可以使用比率z检验进行分析。
比率z检验可以分为单样本率z检验和两样本率z检验。单样本率z检验研究的是样本所在的总体率与已知总体率之间的差异性；两样本率z检验是研究两组比率之间的差异性。很明显，本案例应该使用两样本率z检验进行分析。
三、软件操作及结果解读
（一）理论说明
两样本率z检验的基本原理是：根据假设检验的基本思想首先做检验假设H0：p1=p2；在H0成立的假定下，两个样本率p1、p2的差值p1-p2服从正态分布N\left(0,\sigma_{p_{1}-p_{2}}^{2}\right)，其中\sigma_{p_{1}-p_{2}}^{2}为统计量p1-p2的总体方差。
Z检验的检验统计量：Z=\frac{p_{1}-p_{2}}{\sqrt{\overline{p}\left(1-\overline{p}\right)\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}}
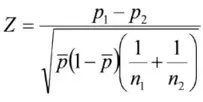
其中：{\overline{{p}}}={\frac{X_{1}+X_{2}}{n_{1}+n_{2}}}
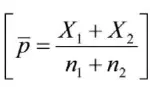
得到z值后，查表得到对应p值，p>0.05时，不拒绝原假设，认为两组比率差异无统计学意义；反之，则认为两组率有统计学意义。
提示：z统计量的公式仅在样本量足够大时适用。即n1*p1、n1*(1-p1)、n2*p2、n2*(1-p2)全都大于5时可以使用。当样本样本量较小时，假设检验需采用Fisher精确概率检验法进行比较。
本案例中试验组两周缓解76人（n1*p1）>5；两周未缓解105-76=29人（n1*(1-p1)）>5。果乳糖组两周缓解49人（n2*p2）>5；两周未缓解111-49=62人（n2*(1-p2)）>5。所以满足大样本前提条件，可以使用两样本率z检验。
（二）软件操作
在SPSSAU实验/医学研究模块，选择【比率z检验】，选择【两样本率z检验】。在“第1组”和“第2组”下，填写案例数据。操作如下图：
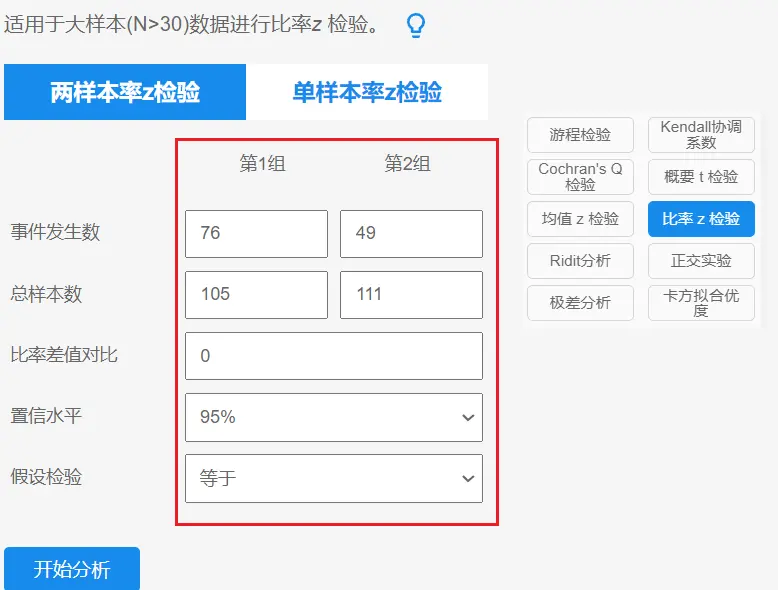
（三）结果解读
SPSSAU首先输出两样本率z检验差值的置信区间如下表：
本次对比试验组和对照组两周缓解率是否有明显差异；试验组的两周缓解率为72.38%，对照组的两周缓解率为44.14%，两组的比率差值为28.24%，并且95%置信区间为(95% CI:0.1565~0.4083)。意味着试验组和对照组两周缓解率的差值在95%的把握水平下应该介于15.65%%到40.83%之间。通常该表格意义较小。
SPSSAU输出两样本率z检验结果如下：
从上表可以，利用两样本率z检验分析两组比率是否有差异，得到z=4.2007，p=0.000<0.05，所以拒绝原假设，接受备择假设，认为两组比率差异有统计学意义。具体可对比试验组和对照组两周缓解率大小进行比较。
四、结论
本案例通过使用两样本率z检验，来分析口服PFG400的试验组和口服乳果糖的对照组治疗后便秘的两周缓解率的差异性，经过研究，得到z=4.2007，p=0.000<0.05，所以拒绝原假设，认为差异有统计学意义，即可以认为口服PFG的患儿人群便秘的两周缓解率高于口服乳果糖的患儿人群。需要注意的是，这只是通过统计方法得到的结论，至于试验组的便秘两周缓解率72.4%和对照组的44.1%的差异有无临床意义，需要儿科专家给出专业性结论。
五、知识小贴士
（1）单样本率z检验如何做？
单样本率z检验研究的是样本所在的总体率与已知总体率之间的差异性；例如某市568名应征男青年中出现视力不良者362名，问该市应征男青年视力不良患病率是否不同于全国患病率50.2%？此类分析应该使用单样本率z检验。与两样本率z检验的区别在于z统计量计算公式和假设检验的不同，在SPSSAU中的操作类似。只需要输入相关数据即可得到分析结果。
（2）比率差值对比、置信水平和假设检验什么意思？
①对比率 (比率差值对比)：两样本率z 检验时，对比数字是指两组比率的差值，与某个预期比率进行对比，通常情况下是0（即两组比率的差值，与数字0进行对比PK，即假设两组比率相等的意思）。真奇怪
②置信水平：指在多大程度上对假设有把握，通常为95%，可选为99%和90%。
③假设检验：原假设是等于，小于，还是大于，通常情况下等于（即直接对比是否相等，即是否有差异）。
参考文献：
[1]颜红,徐勇勇.医学统计学.第3版[M].人民卫生出版社,2015
