双因素方差分析
方差分析当自变量的个数超过一个时，通常要考虑变量之前的交互作用，那么此时的双因素方差分析称为有交互作用的双因素方差分析。这时进行分析，可能会涉及主效应分析、交互效应分析、简单效应分析、事后多重比较四个方面；今天来学习一下，有交互作用的双因素方差分析应该如何分析。
一、基本理论
考虑两个定类数据（自变量）对定量数据（因变量）的影响时，使用的方差分析称为双因素方差分析。与单因素方差分析不同之处在于，双因素方差分析同时考虑两个自变量对因变量的影响，且需要考虑两自变量之间是否有交互效应。
一般来讲，双因素方差分析可以进行主效应分析、交互效应分析、简单效应分析、以及事后多重比较。
- 主效应：一个自变量的不同水平引起因变量产生的差异情况
- 交互效应：两个自变量的搭配对因变量产生的差异情况
- 简单效应：一个自变量在某个水平时，另一个自变量在不同水平下因变量差异情况
- 事后多重比较：一个自变量的不同水平之间两两因变量差异的比较
提示：当主效应存在时，可以进行事后多重比较；当交互效应存在时，可以进行简单效应分析。
二、双因素方差分析案例
案例说明：假设有A、B、C、D四种施肥方式，3种水稻品种，现在想要研究不同施肥方式和不同品种水稻之间产量是否有差异，以及施肥方式和品种的交互作用对水稻产量是否有影响，根据研究目的可以知道，应该选择双因素方差分析进行研究。选择相同状况的土地进行试验，将得到的试验数据整理成如下格式：
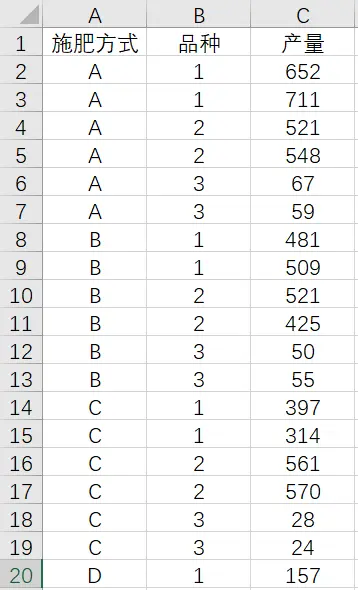
虚拟数据，教学演示
当存在两个变量时，应该首先考虑有交互效应的双因素方差分析模型。将数据上传至SPSSAU系统，选择双因素方差分析，将变量拖拽到相应分析框中后，同时勾选【二阶效应】和【简单效应】，事后多重比较选择【LSD】比较法，操作如下图：
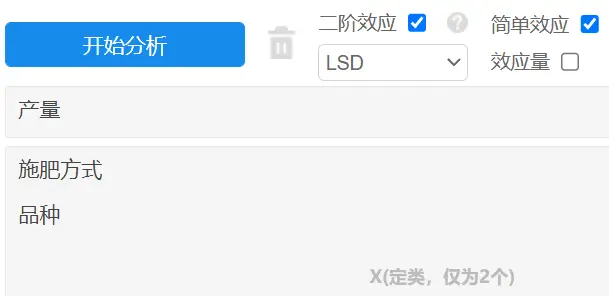
点击开始分析，SPSSAU即可输出双因素方差分析结果。
1、主效应
双因素方差分析中，我们将实验中由一个自变量的不同水平引起因变量产生的差异称为主效应。
SPSSAU输出有交互效应的双因素方差分析结果如下：
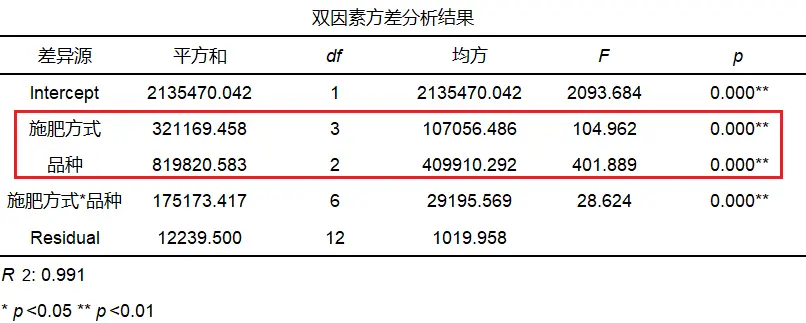
从上表可以看出：施肥方式呈现出显著性(F=104.962，p=0.000<0.05) ，说明施肥方式的主效应存在，施肥方式会对产量产生差异关系；品种呈现出显著性(F=401.889，p=0.000<0.05) ，说明品种的主效应存在，品种会对产量产生差异关系。
2、交互效应
双因素方差分析中，我们将两个自变量的搭配对因变量产生的差异称为交互效应（也称二阶效应）。
从下表看出，施肥方式和品种的交互项呈现出显著性(F=28.624，p=0.000<0.05)，说明施肥方式和品种的交互效应对实验结果的影响是显著的，即交互效应存在。
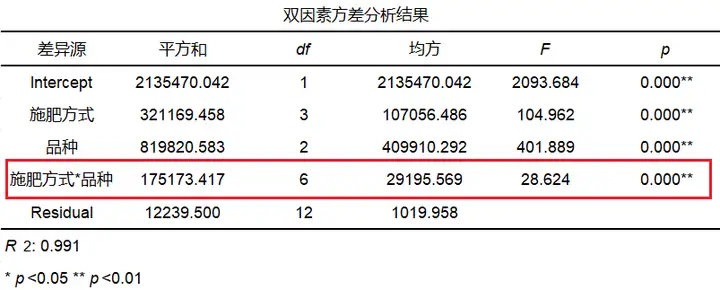
除查看交互项显著性进行交互效应分析，还可以通过查看施肥方式和品种的均值对比图判断是否存在交互效应。从下图可以看出，3条折线并不平行，可以认为存在交互效应，结论和双因素方差分析交互项显著性检验结果一致。
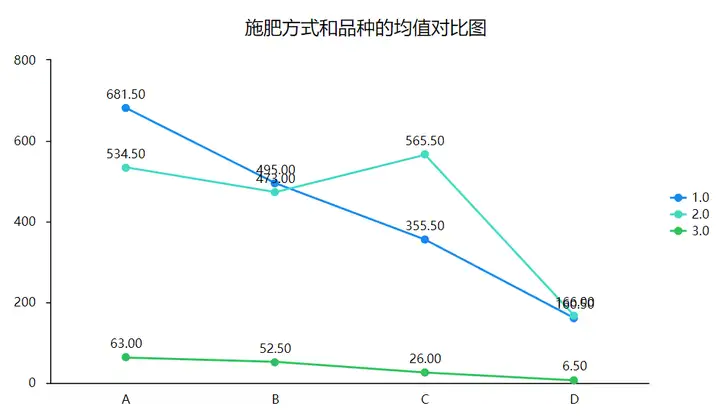
3、简单效应
当交互效应呈现出显著性时，可以进一步进行简单效应分析；当交互效应没有呈现出显著性时，一般不进行简单效应分析。
简单效应是指一个自变量在某个水平时，另一个自变量在不同水平下因变量差异的比较。
下表为固定某种施肥方式，进行两两水稻品种之间的简单效应分析。分析下表结果，当施肥方式为A时，品种1和品种2之间的产量呈现出显著差异（p=0.002<0.05）；当施肥方式为B时，品种1和品种2之间的产量没有呈现出显著差异（p=1.000>0.05）。其他结果解读方式与之类似。
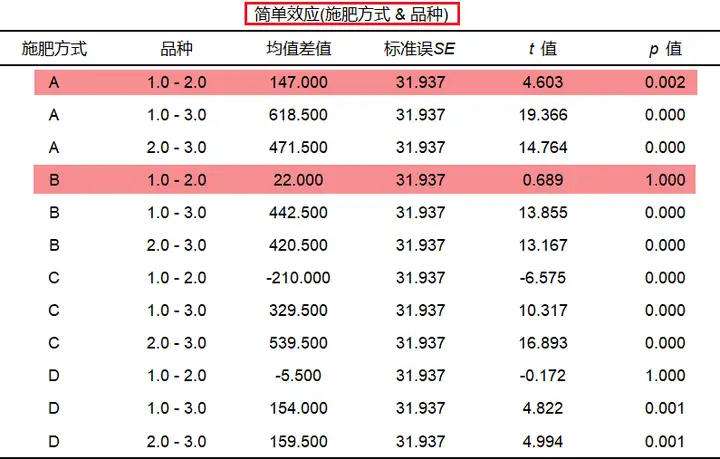
同理，可以固定某种水稻品种，进行两两施肥方式之间的简单效应分析，分析下表结果，当水稻品种为1时，施肥方式A和B之间的产量呈现出显著差异（p=0.000<0.05）；当品种为2时，施肥方式A和B之间的产量没有呈现出显著差异（p=0.469>0.05）。其他结果解读方式与之类似。
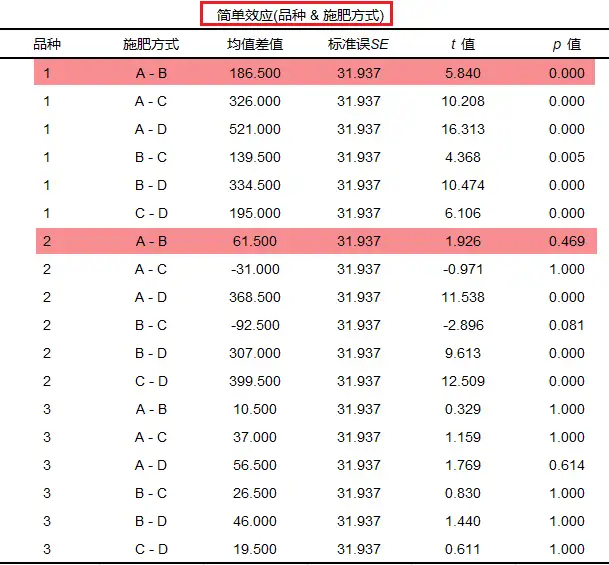
4、事后多重比较
当主效应存在时，我们想知道具体是哪几个组之间存在差异，这就涉及到因素的不同水平之间两两差异比较，称为事后多重比较。
比如在本案例中，我们知道施肥方式的主效应存在，那么说明不同施肥方式的产量之间存在显著差异。但是施肥方式有4种，如果想知道具体哪两种施肥方式之间存在显著差异，那就需要进行事后多重比较。
下表为施肥方式的事后多重比较。分析下表可知，施肥方式A和B之间呈现出显著性差异（p=0.001<0.05）；而施肥方式B和C之间未呈现出显著性差异（p=0.209>0.05）。其他结果解读方式与之类似。
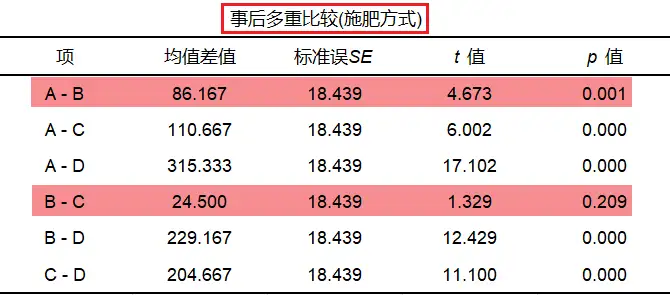
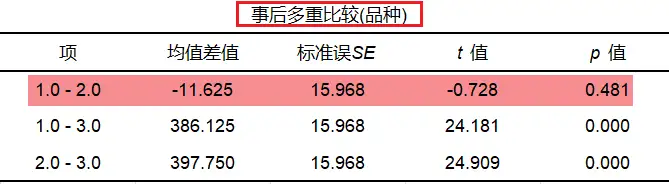
同理，品种的主效应存在，可以进行品种的事后多重比较。分析下表可知，品种1和2之间未呈现显著性差异（p=0.481>0.05），其他结果解读方式与之类似。
补充说明：事后多重比较的方法有很多种，SPSSAU目前提供7种事后多重比较方法，其中最常用的为LSD法，具体说明可参考下方SPSSAU帮助手册：
三、计算公式
设影响因素A有I个水平，影响因素B有J个水平。如果每种水平组合重复测量的次数相同，那么将重复次数记为K(K≥2) ，这时两个影响因素的 IJ 种不同水平组合共有IJK个观测值。
有交互作用的双因素方差分析计算如下表：
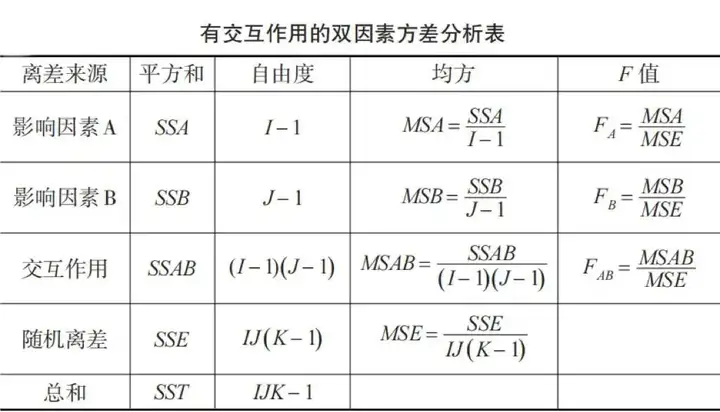
各平方和的计算公式如下：
参考文献：
